2. Дифференциальное уравнение упругой линии.

Граничные условия.

Кривизну упругой линии можно выразить через по известной формуле из курса математики

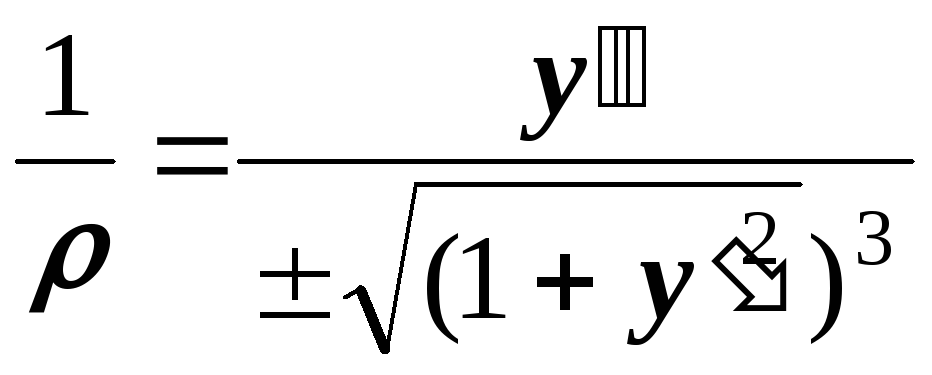. (1)

Если известно уравнение упругой линии , легко вычислить , но нам нужно решить обратную задачу.

При расчете балок на прочность получена зависимость, связывающая кривизну оси балки с изгибающим моментом

(2)

Приравниваем два выражения для кривизны (1) и (2)

(3)

Получили дифференциальное уравнение упругой линии.

В случае малых деформаций уравнение (3) можно упростить , соответственно .

Уравнение (3) принимает вид

(4)

Это приближенное дифференциальное уравнение упругой линии. Знак в уравнении зависит от выбранной системы координат.

Если ось направлена вверх, знак кривизны совпадает со знаком изгибающего момента, в уравнении берут знак плюс (рис. 69). В дальнейшем будем использовать только такую систему координат и всегда брать уравнение в виде

(5)

При интегрировании дифференциального уравнения второго порядка будем получать две постоянных интегрирования и . Для их определения используют условия закрепления концов и сопряжения участков.

В

Рис. 69.

жесткой заделке прогиб и угол поворота равны нулю.

,

На опорах прогибы равны нулю, а углы поворота не равны нулю и должны быть вычислены (рис. 70):

Н

Рис. 70.

а границе участков прогибы и углы поворота соседних сечений совпадают, так как изогнутая ось - непрерывная плавная кривая.

;

3. Определение прогибов непосредственным интегрированием

уравнения упругой линии (пример)

Задана балка на двух опорах, загруженная равномерно распределенной нагрузкой (рис. 71). Пусть известны:

.

Вычислить максимальный прогиб. Решение:

1. Находим опорные реакции

Рис. 71.

2. Составляем и интегрируем дифференциальное уравнение упругой линии

;

3. Определяем и из граничных условий

1)

2);

4. Записываем уравнение прогибов и углов поворота

,

.

5. Определяем максимальный прогиб.

По условию симметрии прогиб максимальный в середине балки, для его вычисления подставляем в уравнение .

.

3. Метод уравнивания произвольных постоянных

(правила Клебша)

Пусть на балку действует несколько нагрузок (рис. 72).

Точки приложения сил делят балку на несколько участков. Аналитические выражения моментов по участкам будут разные

;

Рис. 72.

Соответственно дифференциальное уравнение упругой линии надо составлять по участкам

При интегрировании каждого уравнения получим по две постоянных интегрирования

Если балка имеет участков, то при интегрировании получаем произвольных постоянных , для определения которых надо составить и решить систему уравнений, используя условия закрепления и сопряжения участков. В практических расчетах это неудобно.

Существуют правила позволяющие уменьшить число постоянных до двух при любом числе участков, при этом будут равны между собой все постоянные первого интегрирования и второго

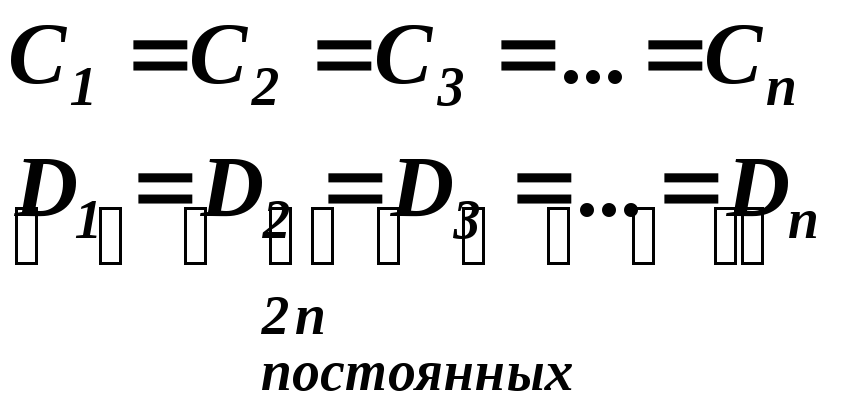
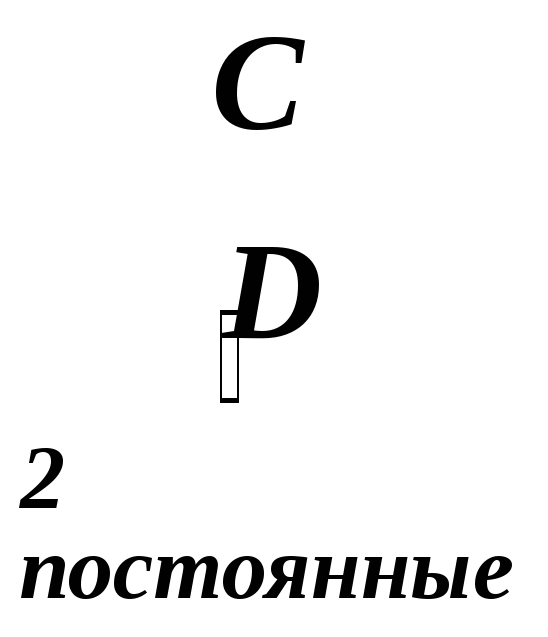
Правила уравнивания постоянных /правила Клебша/.

1. Начало координат выбирается на конце балки (справа или слева безразлично);

2. При составлении выражений для моментов всегда рассматривается часть балки, содержащая начало координат;

3. Сосредоточенный момент надо умножить на скобку , где – координата точки приложения момента;

4. Интегрирования дифференциальных уравнений производят, не раскрывая скобок

5. Если распределенная нагрузка не доходит до конца балки (рис. 73), противоположного началу координат, ее надо продолжить, а чтобы равновесие не нарушилось добавить еще противоположную нагрузку

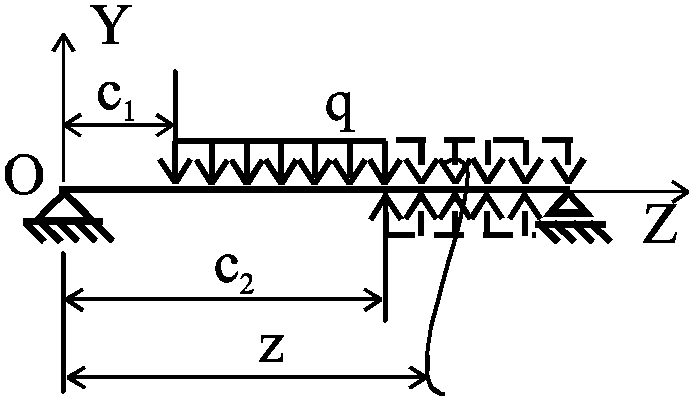
Рис. 73.

Пример: Проверим, что постоянные уравниваются только при соблюдении перечисленных правил (рис. 74).

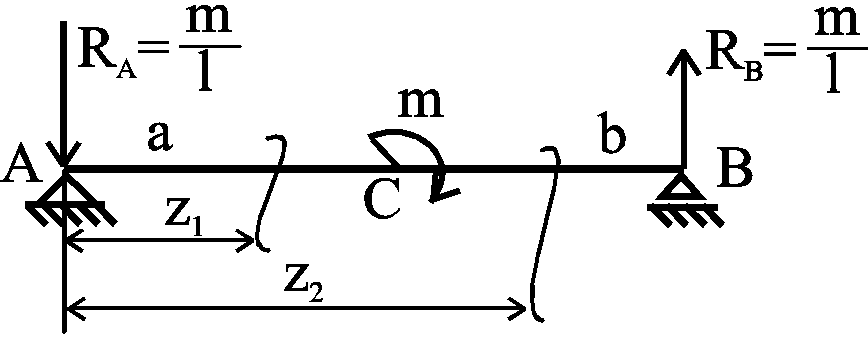
Рис. 74.

:

:

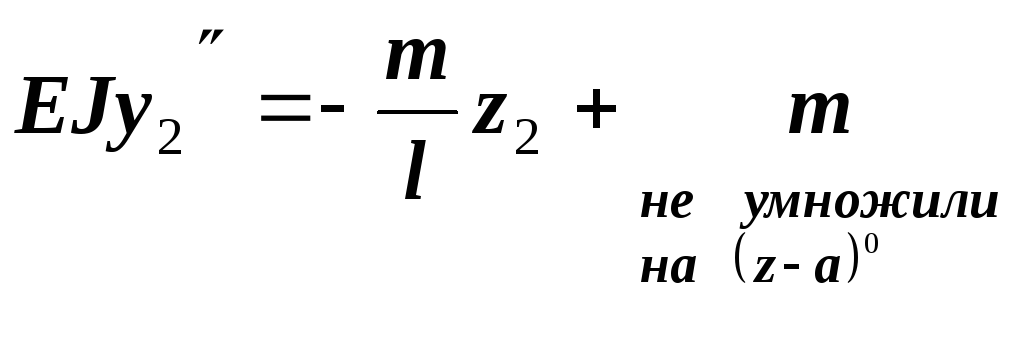
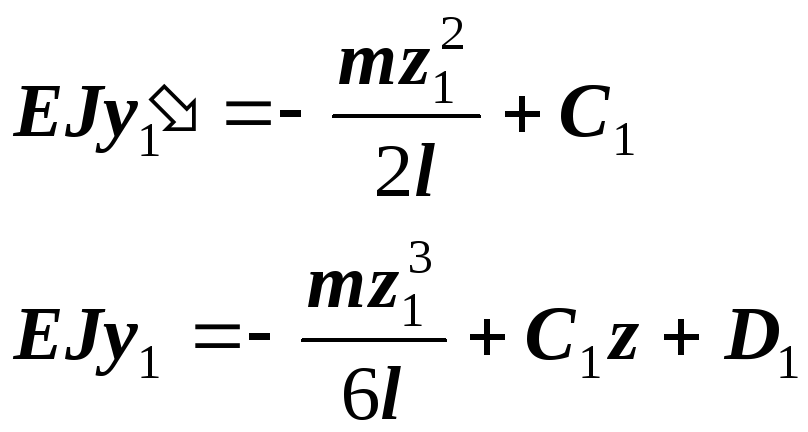
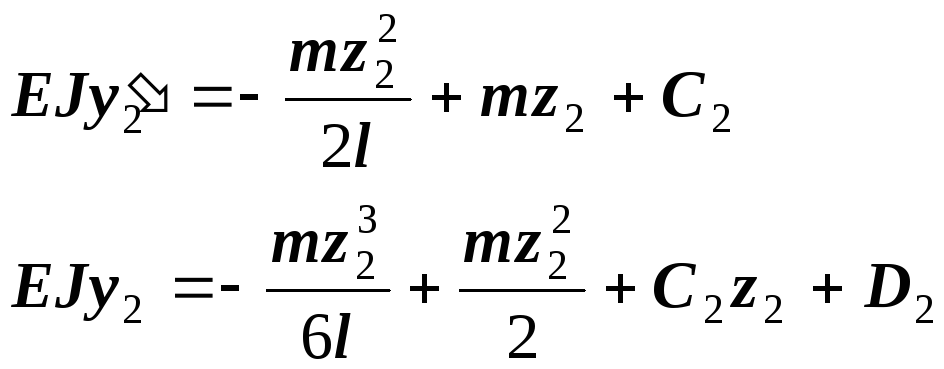
Постоянные не уравнялись, так как не выполнено правило 3.

Составляем и интегрируем уравнения, выполняя правила:

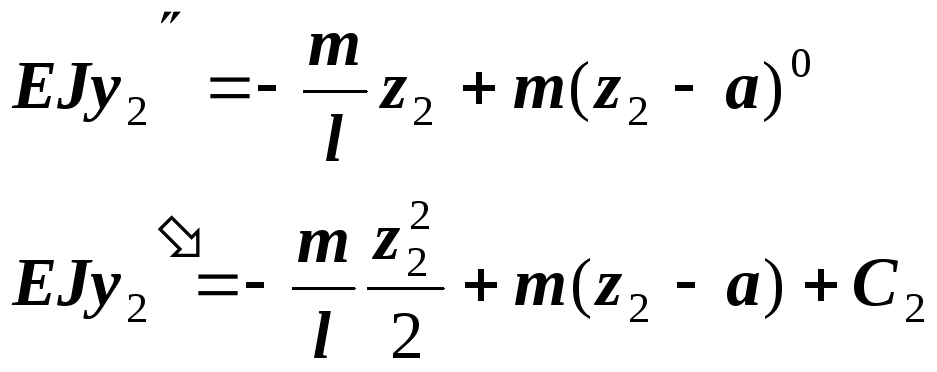
Постоянные уравнялись, так как правила уравнивания соблюдены.