
- •1. Особливості та принципи економетри моделювання економ систем і процесів.
- •2. Поняття економетричної моделі її складові
- •3. Причина,які спонукають появу стохастичної складової
- •4. Етапи побудови економетричної моделі
- •6. Модель пропозиції та попиту
- •7. Модель Кейнса
- •8. Прогнозування: суть методи, класифыкацыйны ознаки
- •9. Використання економетричних моделей для прийняття управлінських рішень
- •10. Метод найменших квадратів та передумови його використання
- •12. Властивості оцінок параметрів
- •13. Умови Гаусса-Маркова для економетричних моделей парної та множинної регресії
- •14. Економетрична модель парної лінійної регресії
- •15. Оцінювання параметрів парної регресійної економетричної моделі за мнк
- •16. Розрахунок та аналіз значень коефіцієнтів детермінації та кореляції.
- •17. Перевірка адекватності моделі парної регресії та статистичної значимості оцінок її параметрів, коєфіцієнтів детермінації та кореляції.
- •18. Перевірка значущості оцінок параметрів моделі та побудова довірчих інтервалівдля оцінок параметрів моделі
- •19. Прогнозування на основі економетричних моделей парної регресії. Точкових та інтервальних прогноз.
- •20 Економчних аналіз моделі парної регресії: середня ефективність впливу чинників, гранична ефективність та коефіцієнти еластичності
- •21)Економетрична модель множинної лінійної регресії.
- •22)Оцінювання параметрів множинної регресійної економетричної моделі за мнк.
- •23)Коефіцієнти детермінації та кореляції множинної економетричної моделі, їх аналіз. Скоригований коефіцієнт детермінації.
- •Перевірка гіпотез про статистичну значимість лінійної моделі множинної регресії, коефіцієнтів регресії, коефіцієнта детермінації, коефіцієнта кореляції.
- •Перевірка гіпотез про значення коефіцієнтів регресії множинної регресійної моделі. Інтервали надійності для коефіцієнтів множинної регресії. ;
- •26.Прогнозування на сонові економетрични моделей множинної регресії. Точковий та інтервальний прогноз
- •27.Економічний аналіз моделі множинної регресії: середня ефективність впливу чинників, гранична ефективність, коефіцієнти еластичності.
- •28Нелінійні моделі. Лінеаризація нелінійних моделей.
- •29.Поліноміальні модель, побудова оцінок її параметрів.
- •30. Гіперболічна модель
- •31. Показникові моделі, побудова оцінок її параметрів.
- •Виробнича функція Кобба-Дугласа, побудова оцінок її параметрів.
- •Метод максимальної правдоподібності.
- •34.Застосування нелінійних функцій в економіці
- •35. Врахування якісних факторів в лінійних економетричних моделях за допомогою фіктивних змінних.
- •Моделі з фіктивними незалежними змінними: моделі, що містять тільки якісні незалежні змінні.
- •37/Моделі з фіктивними незалежними змінними: моделі в яких незалежні змінні носять як якісний так і кількісний характер.
- •38) Порівняння 2-х регресій. Тест Чоу.
- •39. Моделі з фіктивними залежними змінними. Модель lpm
- •41. Моделі з порушенням передумов використання мнк: мультиколінеарність
- •42. Cуть мультиколінеарності
- •43. Наслідки мультиколінеарності
- •44. Ознаки регресійної моделі які вказують на наявність мультиколінеарності
- •45 .Алгоритм Фаррара - Глобера
- •46. Методи звільнення від мультиколінеарност.
- •47 Метод гребеневої регресії усунення мультиколінеарності.
- •48. Моделі з порушенням передумов використання мнк: гетероскедастичність залишків.
- •49. Суть гетероскедастичності
- •50. Наслідки гетероскедастичності
- •51 .Методи визначення гетероскедастичності, тест рангової кореляції Спірмена
- •52.Методи виявлення гетероскедастичності, тест Парка
- •53.Методи виявлення гетероскедастичності, тест Голдфелда-Квандта.
- •55.Метод зважених найменших квадратів оцінювання параметрів моделі з гетероскедастичними залишками при невідомих дисперсіях відхилень спостережень.
- •56. Моделі з порушенням передумов використання мнк: автокореляція залишків.
- •57. Суть автокореляції
- •58. Наслідки автокореляції
- •59. Способи визначення автокореляції залишків. Критерій Дарбіна – Уотсона
- •60.Крім критерію Дарбіна – Уотсона використовують також критерій фон Неймана:
- •61. Нециклічний коефіцієнт автокореляції
- •62. Метод Ейткена
- •63. Метод перетворення вихідної інформації
- •Поняття часового ряду та специфікація його дослідження. Основні компоненти часового ряду.
- •65. Часові ряди та їх основні числові характеристики.
- •66. Вирівнювання часових рядів. Ковзні середні й автокореляція
12. Властивості оцінок параметрів
Оцінки
параметрів
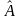 є вибірковими характеристиками і
повинні мати такі властивості:
є вибірковими характеристиками і
повинні мати такі властивості:
1) незміщеності;
2) обгрунтованості;
3) ефективності;
4)
інваріантності.Означення
4.5.
Вибіркова оцінка параметрів
називається незміщеною, якщо вона
задовольняє рівність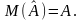
Оскільки
згідно з першою умовою
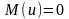 ,
то
,
то
 .
Отже, оцінка параметрів 1МНК є незміщеною.
.
Отже, оцінка параметрів 1МНК є незміщеною.
Різниця між математичним сподіванням оцінки і значенням оціненого параметра
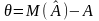 називається
зміщенням оцінки.Не
можна плутати помилку оцінки з її
зміщенням. Помилка дорівнює
називається
зміщенням оцінки.Не
можна плутати помилку оцінки з її
зміщенням. Помилка дорівнює
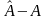 і є випадковою величиною, а зміщення —
величина стала.Дуже
важливою властивістю
оцінки є її обгрунтованість.Означення
4.6. Вибіркова оцінка
параметрів А називається обгрунтованою,
якщо при досить малій величині
і є випадковою величиною, а зміщення —
величина стала.Дуже
важливою властивістю
оцінки є її обгрунтованість.Означення
4.6. Вибіркова оцінка
параметрів А називається обгрунтованою,
якщо при досить малій величині
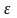 > 0
справджується cпіввідношення
> 0
справджується cпіввідношення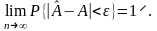 Третя
властивість оцінок Â
— ефективність — пов’язана з величиною
дисперсії оцінокТут доречно сформулювати
важливу теорему Гаусса — Маркова, що
стосується ефективності оцінки
1МНК.Теорема Гаусса — Маркова. Функція
оцінювання за методом 1МНК покомпонентно
мінімізує дисперсію всіх лінійно
незміщених функцій вектора оцінок
:
Третя
властивість оцінок Â
— ефективність — пов’язана з величиною
дисперсії оцінокТут доречно сформулювати
важливу теорему Гаусса — Маркова, що
стосується ефективності оцінки
1МНК.Теорема Гаусса — Маркова. Функція
оцінювання за методом 1МНК покомпонентно
мінімізує дисперсію всіх лінійно
незміщених функцій вектора оцінок
:
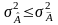 для
Означення
4.7. Вибіркова оцінка
параметрів А називається ефективною,
коли дисперсія цієї оцінки є найменшою.
для
Означення
4.7. Вибіркова оцінка
параметрів А називається ефективною,
коли дисперсія цієї оцінки є найменшою.
Нехай
ефективна оцінка параметрів
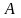 ,
а
,
а
 — деяка інша оцінка цих параметрів.
Тоді
— деяка інша оцінка цих параметрів.
Тоді
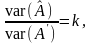
Означення
4.8. Незміщена оцінка
,
дисперсія якої при
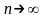 задовольняє умову
задовольняє умову
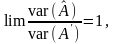 називається асимптотично ефективною
оцінкою.
називається асимптотично ефективною
оцінкою.
Ще
одна важливість оцінок — їх
інваріантність.Означення
4.8. Оцінка
параметрів
називається інваріантною, якщо для
довільно заданої функції
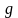 оцінка параметрів функції
оцінка параметрів функції
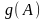 подається у вигляді
подається у вигляді
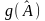 .
Іншими словами, інваріантність оцінки
базується на тому, що в разі перетворення
параметрів
за допомогою деякої функції
таке саме перетворення, виконане щодо
,
дає оцінку
нового параметра.
.
Іншими словами, інваріантність оцінки
базується на тому, що в разі перетворення
параметрів
за допомогою деякої функції
таке саме перетворення, виконане щодо
,
дає оцінку
нового параметра.
13. Умови Гаусса-Маркова для економетричних моделей парної та множинної регресії
Тут доречно сформулювати важливу теорему Гаусса — Маркова, що стосується ефективності оцінки 1МНК.
Теорема Гаусса — Маркова. Функція оцінювання за методом 1МНК покомпонентно мінімізує дисперсію всіх лінійно незміщених функцій вектора оцінок :
для ,
де
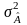 — дисперсія оцінок
,
визначених згідно з 1МНК,
— дисперсія оцінок
,
визначених згідно з 1МНК,
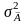 — дисперсія оцінок
— дисперсія оцінок
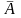 ,
визначених іншими методами.
,
визначених іншими методами.
Отже, функція оцінювання 1МНК у класичній лінійній моделі є найкращою (мінімально дисперсійною) лінійною незміщеною функцією оцінювання. (Цю властивість називають BLUE).
З
означення дисперсії випливає, що
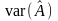 — параметр розподілу випадкової
величини А,
яка є мірою розсіювання її значень
навколо математичного сподівання.
— параметр розподілу випадкової
величини А,
яка є мірою розсіювання її значень
навколо математичного сподівання.
14. Економетрична модель парної лінійної регресії
Розглянемо випадок лыныйного економетричного моделы з двома змынними: y=ao+a1x+U. даны моделы набули широкого вжиту в економыцы завдяки своъй простоты. Часто такы моделы є складовими більш складних моделей. У такій моделі змінною пояснювальною змінною або регресором є Х. Залежною змінною або регресантом є У. Модель називається теоретичною лінійною моделлю парної регресії.
Для визначення теоретичних коеф а0 та а1 необхідна наявність повної вибірки сукупності хі і відповідних їх значень уі. Але так як це практичнор неможливо то будуються оцінки аоц – а0 , аоц1-а1 теоретичних змінних на основі вибірки хі та уі з генеральної сукупності значень змінних Х та У.
Отже теоретично модель подана вище, в яку входять замість параметрів їх оцінки наз емпіричною моделлю. І Має вигляд аналогічно тіки з оцінками. Щоб ця модель була найближчою до оригіналу то оцінки будуються тіки за МНК.
