27.Економічний аналіз моделі множинної регресії: середня ефективність впливу чинників, гранична ефективність, коефіцієнти еластичності.
Коефіцієнт еластичності. Ke – це границя відношення зміни у відсотках залежної змінної при зміні на 1% незалежної змінної.
Ke
*
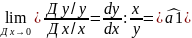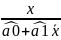
Часто під Ke розуміють число
Ke
=
*
=
*
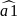Величини
=
=
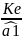наз коефіцієнтом
середньої ефективності
впливу x на y і визначає обєм величини
у який приходиться на одиницю обєму
незалежної змінної ч в середньому.
Величина
Кге=
наз граничною
ефективністю.
Вона визначає зміну залежної змінної
у за рахунок зміни незалежної змінної
х на одиницю.
Множинна регресія
Величина
Кеі
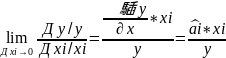наз частинами коеф еластичності.
К еі – еластичність впливу регресора
Еі не регресант у. Вона визначає як зміниться залежна змінна у %, коли незалежна змінна хі зміниться на 1%
Часто під К еі розуміють число
К
еі = аі *
Сумарним коеф. Еластичності наз. Величина:
Ке = ∑Кеі
Частинний коеф середньої ефективності визн. За формулою:
К
=
=
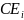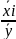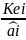
К
=
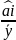
28Нелінійні моделі. Лінеаризація нелінійних моделей.
Внаслідок складності економічних процесів лінійні моделі не завжди коректно описують залежність регресанта від регресора .
Зокрема найбільш конкретними моделями є:
1.Лінійна модель
У = а0 + а1х +е залежність попиту у від ціни х
1.Степенева модель
У
= а1
+ е
використов для дослідження еластичності
залежності попиту від ціни.
1.Колінонеальна модель
У
= а0+а1х +а2
+ …+
+ е
Залежність витрат у від обсягів виробництва х
1.Вироб ф-ція Кобба Дугласа
У
= а0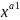
+
е
Обсяг вироб. у від витрат капіталу zі і трудових ресурсів х .
29.Поліноміальні модель, побудова оцінок її параметрів.
У
= а0 + а1х + а2
+ ..+
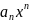+ е
Подається у матричній формі
У = ХА + е
х
=
A
=
y=
Ці моделі теоретичні.
Емпірична модель матиме вигляд :
=
Х
X
=
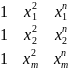
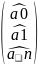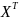
у=
; (
У
30. Гіперболічна модель
Уі=а0+а1 1/х+Еі і=1,n
Цю модель можна записати у вигляді
Х=1 1/х1
1 1/х2
. .
. .
. .
1 1/хn
У=хА+Е
Умод.=х*Амод
Амод=а0мод
а1мод -емпірична
у мод=а0мод+а1мод*1/х тоді
1)якщо а0мод<0, а1мод>0 ця модель називається Моделлю Філіпса-викор.для опису залежності між зміною з/п «у» та рівнем безробіття «х».
2)якщо а0мод>0, а1мод<0 модель Торнквіста
Така модель описує залежність між попитом на товари першої необхідності та доходом.
3) а0мод>0, а1мод>0 – гіпербола
Описує зв'язок між середніми фіксованими витратами «у»та обсягом випуску прод-ї «х».