Сплошной (тормозной) рентгеновский спектр

Рентгеновское излучение

Источник рентгеновского излучения—рентгеновская трубка. Ускоренные электрическим полем электроны бомбардируют анод (металлическая мишень из тяжелых металлов, например W или Pt), испытывая на нем резкое торможение. При этом возникает рентгеновское излучение, представляю­щее собой электромагнитные волны с длиной волны примерно 10^-12—10^-8 м. Волновая природа рентгеновского излучения доказана опытами по его дифракции.

Рентгеновский спектр

Наложение сплошного спектра (см. рисунок), ограниченного со стороны коротких длин волн некоторой границей, называемой границей сплошного спектра, и линейчатого спектра — совокупности отдельных линий, появляющихся на фоне сплошного спектра.

Сплошной (тормозной) спектр

Испускается бомбардирующими анод электронами в результате их торможения при взаимодействии с атомами мишени. Не зависит от материала анода, а определяется только энергией бомбардирующих анод электронов. Согласно классической теории, действительно при торможе­нии движущихся зарядов должно возникать излучение со сплошным спектром.

К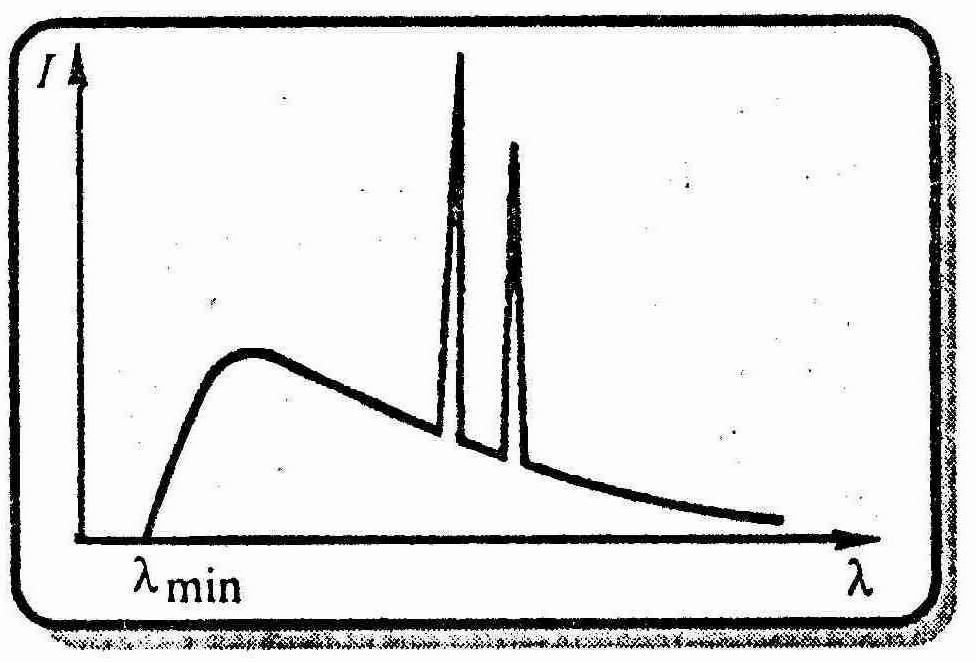 оротковолновая граница сплошного спектра

Из классической теории существо­вание λ_min не вытекает. Из опыта: чем больше кинетическая энергия элект­ронов, вызывающих тормозное рентгеновское излучение, тем мень­ше λ_min Согласно квантовой теории, предельная энергия кванта соот­ветствует такому случаю торможе­ния, при котором вся кинетическая энергия электрона переходит в энергию кванта, т. е.

• где U — разность потенциалов, за счет которой электрону сообщается энергия Е_max, — частота, соответствующая границе сплошного спектра. Тогда

что полностью соответствует экспериментальным данным.

Характеристический рентгеновский спектр. Закон Мозли

При достаточно большой энергии бомбардирующих анод электронов на фоне сплошного спектра появляются отдельные резкие линии — линейчатый спектр, определяемый материалом анода, — характеристический рентгеновский спектр.

Эти спектры совершенно однотипны и состоят из нескольких серий, обо­значаемых К, L, M, N и О. Каждая серия, в свою очередь, содержит небольшой набор отдельных линий, обозначаемых в порядке убывания длины волны индексами α,β,γ,... (К_α, K_β, K_γ..., L_α, L_β, L_γ, ...) (см. рисунок). Возникновение харак­т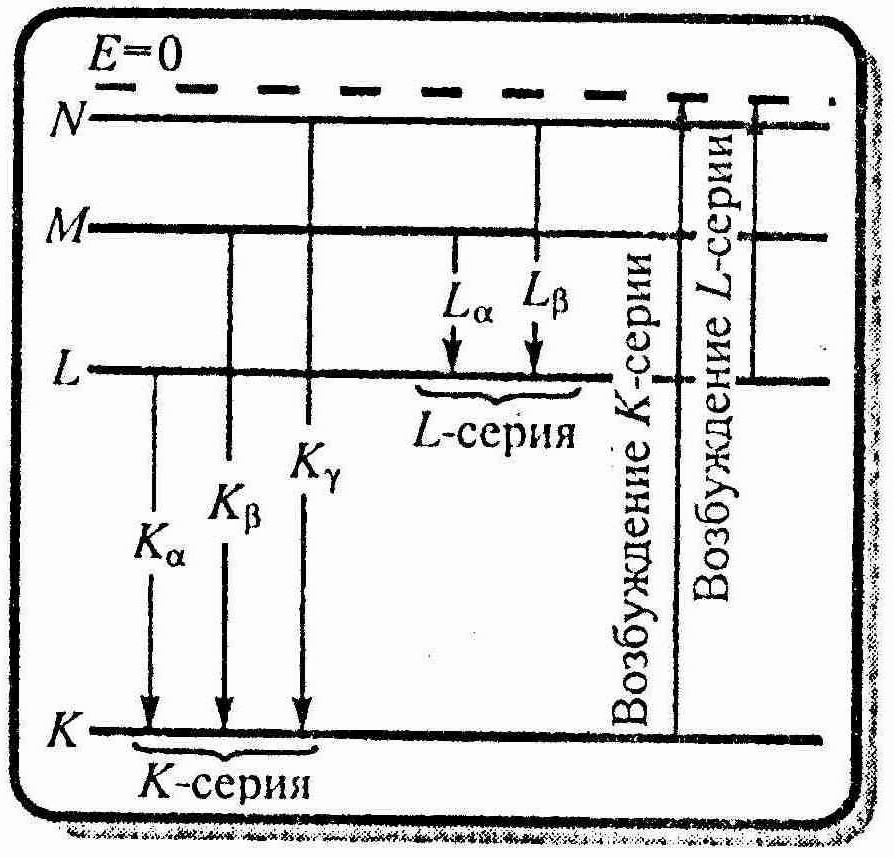 еристических рентгеновских спектров связано с процессами, происходящими во внутренних, застроенных электрон­ных оболочках атомов, которые имеют сходное строение.

Самой длинноволновой линией K-серии является линия К_α. Частоты линий возрастают в ряду К_α → K_β→K_γ, поскольку энергия, высвобождаемая при переходе электрона на К-оболочку с более удаленных оболочек, увеличивается. Наоборот, интенсивности линий в ряду К_α → K_β→K_γ убывают, так как вероятность переходов электронов с L,-оболочки на K-оболочку больше, чем с более удаленных оболочек М и N. K-серия сопровождается обязательно другими сериями, так как при испускании ее линий появляются вакансии в оболочках L, М,..., которые будут заполняться электронами, находящимися на более высоких уровнях.

З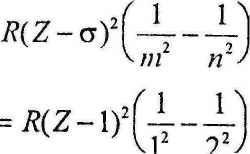 акон Мозли

определяет число спектральных линий характеристического рентгеновского излу­чения

Для линии К_α (σ=1);

[R — постоянная Ридберга; Z — порядковый номер элемента в периоди­ческой системе; σ — постоянная экранирования; m характеризует рент­геновскую серию (m = 1, 2, 3, ...); n определяет отдельные линии соот­ветствующей серии (n =m+1, m + 2,...)].

Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, соответствующий некоторой линии, действует не весь заряд ядра Ze, а заряд (Z- σ)е, ослабленный экранирующим действием других электронов.