16.4.Нескінчено велика функція (н.В.Ф.)

Функція називається нескінченно великою при , якщо для будь-якого числа M>0 існує число , що для всіх х, задовольняючих нерівності , виконується нерівність . Записують або при .

Коротко :

Наприклад, функція є н.в.ф. при х®2.

Якщо f(x) прагне нескінченності при і приймає лише додатні значення, то пишуть ; якщо лише від’ємні значення, то

Функція , задана на всій числовій прямій, називається нескінченно великою при , якщо для будь-якого числа М>0 знайдеться таке число N=N(M)>0, що при всіх х, задовольняючих нерівності |x|>N, виконується нерівність . Коротко :

Наприклад, у=2х є н.в.ф. при

Відзначимо, що аргумент х, прагнучи нескінченності, приймає лише натуральні значення, тобто 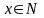, то відповідна н.в.ф. стає нескінченно великою послідовністю. Наприклад, послідовність , є нескінченно великою послідовністю. Очевидно, всяка н.в.ф. в околі точки є необмеженою в цій околу. Обернене твердження невірно :необмежена функція може і не бути н.в.ф. (Наприклад, у=xsinx.).Однако, якщо, де А- скінчене число, то функція f(x) обмежена в околі точки .

Дійсно, з означення границі функції виходить, що при виконується умова Отже, при , а це і означає, що функція f(x) обмежена.

Тема 5.5. Нескінченно малі функції (н. М. Ф.)

5.5.1. Означення і основні теореми.

Функція називається нескінченно малою при , якщо

(17.1)

За означенням границі функції рівність (17.1) означає : для будь-якого числа e>0 знайдеться таке, що для всіх х, задовольняючих нерівності , виконується нерівність .

Аналогічно визначається н.м.ф. при , , , : у всіх цих випадках .

Нескінченно малі функції часто називають нескінченно малими величинами або нескінченно малими; позначають звичайно грецькими буквами a,b і т.д.

Прикладами н.м.ф. служать функції при ; у=х-2 при х®2; y=sinx при х®p до, до є Z.

Інший приклад : , , - нескінченно мала послідовність.

Теорема 17.1.Алгебраическая сума скінченого числа нескінченно малих функцій є нескінченно мала функція.

□ Нехай a(х) і b(х) –дві н.м. функції при . Це значить, що, тобто для будь-кого , а значить, і знайдеться число d₁ >0 таке, що для всіх х, задовольняючих нерівності , виконується нерівність

(17.2)

і, тобто

. (17.3)

Нехай d-найменше з чисел d₁ і d₂. Тоді для всіх х, задовольняючих нерівності , виконуються обидві нерівності (17.2) і (17.3). Отже, має місце співвідношення

Таким чином

.

Це значить, що , тобто a(х)+b(х)-н.м.ф. при _.

Аналогічно проводиться доведення для будь-якого кінцевого числа н.м. функцій.■

Теорема 17.2. Добуток обмеженої функції на нескінченно малу функцію є функція нескінченно мала.

□ Нехай функція f(x) обмежена при .Тогда існує таке число М>0, що

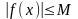(17.4)

для всіх х з d₁-околу точки . І нехай a(х)-н.м.ф. при .Тогда для будь-кого , а значить, і знайдеться таке число d₂>0 що при всіх х, задовольняючих нерівності , виконується нерівність

. (17.5)

Позначимо через d якнайменше з чисел d₁ і d₂. Тоді для всіх х, задовольняючих нерівності виконуються обидві нерівності (17.4) і (17.5). Отже . А це означає, що добуток при є нескінченно мала функція. ■

Наслідок 17.1. Оскільки всяка б.м.ф. обмежена, то з теореми (17.2) витікає : твір двох б.м.ф. є функція нескінченно мала.

Наслідок 17.2. Добуток б.м.ф. на число є функція нескінченно мала.

Теорема 17.3. Частка від ділення нескінченно малої функції на функцію, що має відмінну від нуля границю, є функція нескінченно мала.

□ Нехай, а . Функція може бути представлений у вигляді добутку б.м.ф. a(х) на обмежену функцію . Але тоді з теореми (17.2) витікає, що частка є функція нескінченно мала.

Покажемо, що функція обмежена. Візьмемо e>|a|. Тоді, на підставі визначення границі, знайдеться , що для всіх х, задовольняючих нерівності , виконується нерівність _.А оскільки , то , тобто . Отже

тобто функція - обмежена.■

Теорема 17.4. Якщо функція a(х)- нескінченно мала (a¹0), то функція є нескінченно велика функція і навпаки : якщо функція f(x)- нескінченно велика, то - нескінченно мала.

□ Нехай a(х) є б.м.ф. при тобто . Тоді

,

тобто тобто , де . А це означає, що функція є нескінченно велика. Аналогічно доводиться зворотне твердження. ■

Зауваження : Доведення теорем приводилися для випадку, коли, але вони справедливі і для випадку, коли .

Приклад 17.1. Показати, що функція

при є нескінченно малою.

○ Оскільки , то функція j(х)=(х-1)² є нескінченно мала при . Функція g(х)=sinх є добутком обмеженої функції (g(х)) на нескінченно малу (j(х)). Значить, f(x)- нескінченно мала при .●