Тема 5.6.Еквівалентні нескінченно малі функції

5.6.1. Порівняння нескінченно малих функцій

Як відомо, сума, різниця і добуток двох н.м.ф. є функція нескінченно мала. Відношення ж двох н.м.ф. може поводитися різним чином : бути кінцевим числом, бути нескінченно великою функцією, нескінченно малої або взагалі не прагнути ні якої границі.

Дві н.м.ф. порівнюються між собою за допомогою їх відношення.

Нехай є н.м.ф. при , тобто і

1. Якщо , то і називаються нескінченно малими одного порядку.

2. Якщо 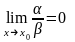, то називається нескінченно малою більш високого порядку, ніж .

3. Якщо , то називається нескінченно малою більш низького порядку, ніж .

4. Якщо не існує, то і називаються незрівнянними нескінченно малими.

Відзначимо, що такі ж правила порівняння н.м.ф. при , .

Приклад 18.1. Порівняти порядок функцій при

○ При це н.м.ф. одного порядку, оскільки

Говорять, що н.м.ф. a і b одного порядку прагнуть нуля з приблизно однаковою швидкістю. ●

Приклад 18.2. Чи є функції н.м.ф. одного порядку при ?

○ При функція є н.м.ф. більш високого порядку, ніж , оскільки . В цьому випадку н.м.ф. прагне нуля швидше, ніж ●

Приклад 18.3. Порівняти порядок функцій при .

○ Оскільки

,

то є н.м.ф. більш низького порядку, ніж ●

Приклад 18.4. Чи можна порівняти функції і b=х при х®0?

○ Функції і при є незрівнянними н.м.ф., оскільки границя не існує. ●

5.6.2.Еквівалентні нескінченно малі і основні теореми про них

Серед нескінченно малих функцій одного порядку особливу роль грають так звані еквівалентні нескінченно малі.

Якщо , то і називається еквівалентними нескінченно малим (при ) ; це позначається так : ~ .

Наприклад, sinx~x при , оскільки ; tgx~x при , оскільки .

Теорема 18.1. Границя відношення двох нескінченно- малих функцій не зміниться, якщо кожну або одну з них замінити еквівалентній їй нескінченно малою.

□ Нехай a ~a^’ і b ~b^' при . Тоді

, тобто .

Очевидно також, що .■

Теорема 18.2. Різниця двох еквівалентних нескінченно малих функцій є нескінченно мала більш високого порядку, ніж кожна з них.

□ Нехай a ~b при Тоді

,

аналогічно . ■

Справедливо і обернене твердження : якщо різниця н.м.ф. a і b є нескінченно мала вищого порядку, ніж або , то і - еквівалентні нескінченно малі.

Дійсно, оскільки, то, тобто Звідси , т. е. a ~b. Аналогічно, якщо???, то a ~b.

Теорема 18.3. Сума скінченого числа нескінченно малих функцій різних порядків еквівалентна доданку низького порядку.

Доведемо теорему для двох функцій.

□ Нехай при , причому a- н.м.ф. вищого порядку, ніж b, тобто Тоді .

Отже a +b ~ b при .

Доданок, еквівалентний сумі нескінченно малих, називається головною частиною цієї суми.

Заміна суми н.м.ф. її головною частиною називається відкиданням нескінченно малих вищого порядку. .■

Приклад 18.5. Знайти границю .

○ Оскільки 3х+7х2~3х і sin 2x~2x при . ●

5.6.3.Застосування еквівалентних нескінченно малих функцій. Обчислення границь.

Для розкриття невизначеності вигляду часто бувають корисним застосовувати принцип заміни нескінченно малих еквівалентними і інші властивості еквівалентних нескінченно малих функцій. Як відомо, sinx~x при , tgx~x при . Проведемо ще приклади еквівалентних н.м.ф.

Приклад 18.6. Покажемо, що при .

○ . ●

Приклад 18.7. Знайдемо .

○ Позначимо arcsin x=t. Тоді x=sint і t®0 при .

Тому

.

Отже, arcsinx~x при . ●

Приклад 18.8. Покажемо, що -1~ при .

○ Оскільки

то -1~ при . ●

Нижче приведені найважливіші еквівалентності, які використовуються при обчисленні границь :

1. sinx~x при ; 6. e^x-1~x ( );

2. tgx~x ( ); 7. a^x-1~x×lna ( );

3. arcsinx~x ( ); 8. ln(1+x)~x ( );

4. arctgx~x ( ); 9. log_a(1+x)~x×logae ( );

5. 1-cosx~ ( ); 10. (1+x)^k- ×x, k>0 ( );

зокрема .

Приклад 18.9. Знайти .

○ Оскільки tgx~2x, sin3x~3x при , то

. ●

Приклад 18.10. Знайти .

○ Отримаємо, з слідує t®0. Тому

. ●

Приклад 18.11. Знайти .

○ Оскільки arcsin (x-1)~(x-1) при х®1, то

. ●

Наближені обчислення

Якщо a ~b, то, відкидаючи в нерівність a =b+(a -b) нескінченно малу високого порядку, тобто a -b, отримаємо наближену рівність a »b.

Воно дозволяє виражати одні нескінченно малі через інші. Приведені вище найважливіші еквівалентності служать джерелом ряду наближених формул.

Приведені формули справедливі при малих х, і вони тим точніше, чим менше х.

Наприклад, графіки функцій y=tgx і y=x в околі точки 0 практично не выдрызняються(див. рис.114), а крива y=sinx в околі точки зливається з прямою y=x (мал. 115). На малюнках 116-118 проілюстровані деякі з найважливіших еквівалентностей, про які мовиться вище.

Приклад 18.12. Знайти наближене значення ln 1,032.

○ ln 1,032=ln(1+0,032) »0,032. Для порівняння результату по таблиці логарифмів знаходимо, що ln 1,032=0,031498. ●