5.7.4. Основні теореми про неперервні функції. Неперервність елементарних функцій

Теореми про неперервність функції випливають безпосередньо з відповідних теорем про границі.

Теорема 1: Сума, добуток і частка двох неперервних функцій є функція неперервна (для частки: за винятком тих значень аргументу, у яких дільник дорівнює нулю).

□ Нехай функції f(x) і (x) неперервні на деякій множині Х, де х₀ - будь-яке значення із цієї множини. Доведемо, наприклад, неперервність добутку F(x)= . Застосовуючи теорему про границю добутку, одержимо:

Отже, 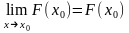, що й доводить неперервність функції в точці.■

Теорема 2: Нехай функція неперервна в точці х₀ , а функція неперервна в точці u₀= (x₀). Тоді складна функція f( (x)), що складається з неперервних функцій, неперервна в точці х_0.

□ У силу неперервності функції , , тобто при х₀ маємо u₀. Тому внаслідок неперервності функції маємо:

Це й доводить, що складна функція f(j(x)) неперервна в точці х₀ .■

Теорема 3: Якщо функція неперервна й строго монотонна на осі Ох, то обернена функція також неперервна й монотонна на відповідному відрізку осі Оу (без доведення).

Так, наприклад, функція , за теоремою 1, є функція неперервна для всіх значень х, крім тих, для яких 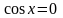, тобто крім значень , n Z.

Функція , за теоремою 3, неперервні при всіх значеннях х , при яких ці функції визначені.

Можна довести, що всі основні елементарні функції неперервні при всіх значеннях х, для яких вони визначені.

Як відомо, елементарною називається така функція, яку можна задати однією формулою, що містить скінчене число арифметичних дій і суперпозицій (операції взяття функції від функції) основних елементарних функцій. Тому з наведених вище теорем випливає: усяка елементарна функція неперервна в кожній точці, у якій вона визначена.

Цей важливий результат дозволяє, знаходити границі елементарних функцій у точках, де вони визначені.

Приклад 19.4 Знайти .

○ Функція 2^ctgx неперервна в точці , тому: ●

5.7.5 Властивості функцій, неперервних на відрізку

Неперервні на відрізку функції мають ряд важливих властивостей. Сформулюємо їх у вигляді теорем, не наводячи доведень.

Т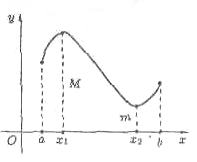 еорема 4: (Вейерштрасса). Якщо функція неперервна на відрізку, то вона досягає на цьому відрізку свого найбільшого й найменшого значення.

Зображена на рис.123 функція неперервна на відрізку , приймає своє найбільше значення М у точці х₁, а найменше -m- у точці х₂. Для будь-якого х має місце нерівність .

Наслідок 19.1: Якщо функція неперервна на відрізку, то вона обмежена на цьому відрізку.

Рис. 123

Теорема 19.5(Больцано- Коші): Якщо функція неперервна на відрізку й приймає на його кінцях нерівні значення й , то на цьому відрізку вона приймає й всі проміжні значення між А та В.

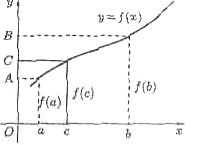
Рис. 124

□ Геометрично теорема очевидна (див. рис. 124).

Для будь-якого числа С, розміщеного між А та В, знайдеться точка с всередині цього відрізка така, що . Пряма перетне графік функції принаймні в одній точці.■

Наслідок 19.2: Якщо функція неперервна на відрізку й на його кінцях приймає значення різних знаків, то усередині відрізка знайдеться хоча б одна точка с, у якій дана функція перетворюється в нуль: .

Наслідок 19.2: Лежить в основі так званого «методу половинного ділення», що використовується для знаходження кореня рівняння

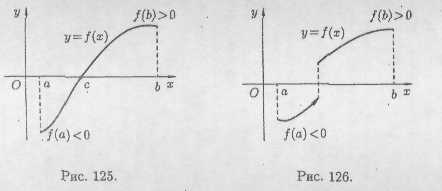
Твердження теорем 19.4 і 19.5, взагалі говорячи, виявляються невірними, якщо порушені хоч якісь із їх умов: функція неперервна не на відрізку , а в інтервалі (a;b), або функція на відрізку має розрив див. рис.126 демонструє це для наслідку теореми 19.5: графік перервної функції не перетинає вісь Ох.

Приклад 19.5. Визначити з точністю до корінь рівняння , що належить відрізку 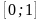, застосувавши метод половинного ділення.

○ Позначимо ліву частину рівняння через .

Крок 1. Обчислюємо й , де .

Крок 2. Обчислюємо . Крок 3. Обчислюємо . Якщо , то - корінь рівняння.

Крок 4. При якщо , то вважаємо, що , інакше

Крок 5. Якщо , то задача вирішена. Як шуканий корінь (із заданою точністю ) приймається величина . Інакше процес ділення відрізка навпіл продовжуємо, повертаючись до кроку 2.

У результаті зроблених дій одержуємо: .●