5.2.5.Складна функція

Нехай функція визначена на множині , а функція на множині , причому для відповідне значення 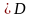. Тоді на множині визначена функція 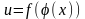, яка називається складною функцією від (або суперпозицією заданих функцій, або функцією від функції ).

Змінну називають проміжним аргументом складної функції.

Наприклад, функція є суперпозиція двох функцій . Складна функція може мати декілька проміжних аргументів.

5.2.6. Основні елементарні функції і їх графіки

Основними елементарними функціями називаються наступні функції.

1. П оказникова функція . На рис. 104 показані графіки показникових функцій, відповідні різним показникам степеня.

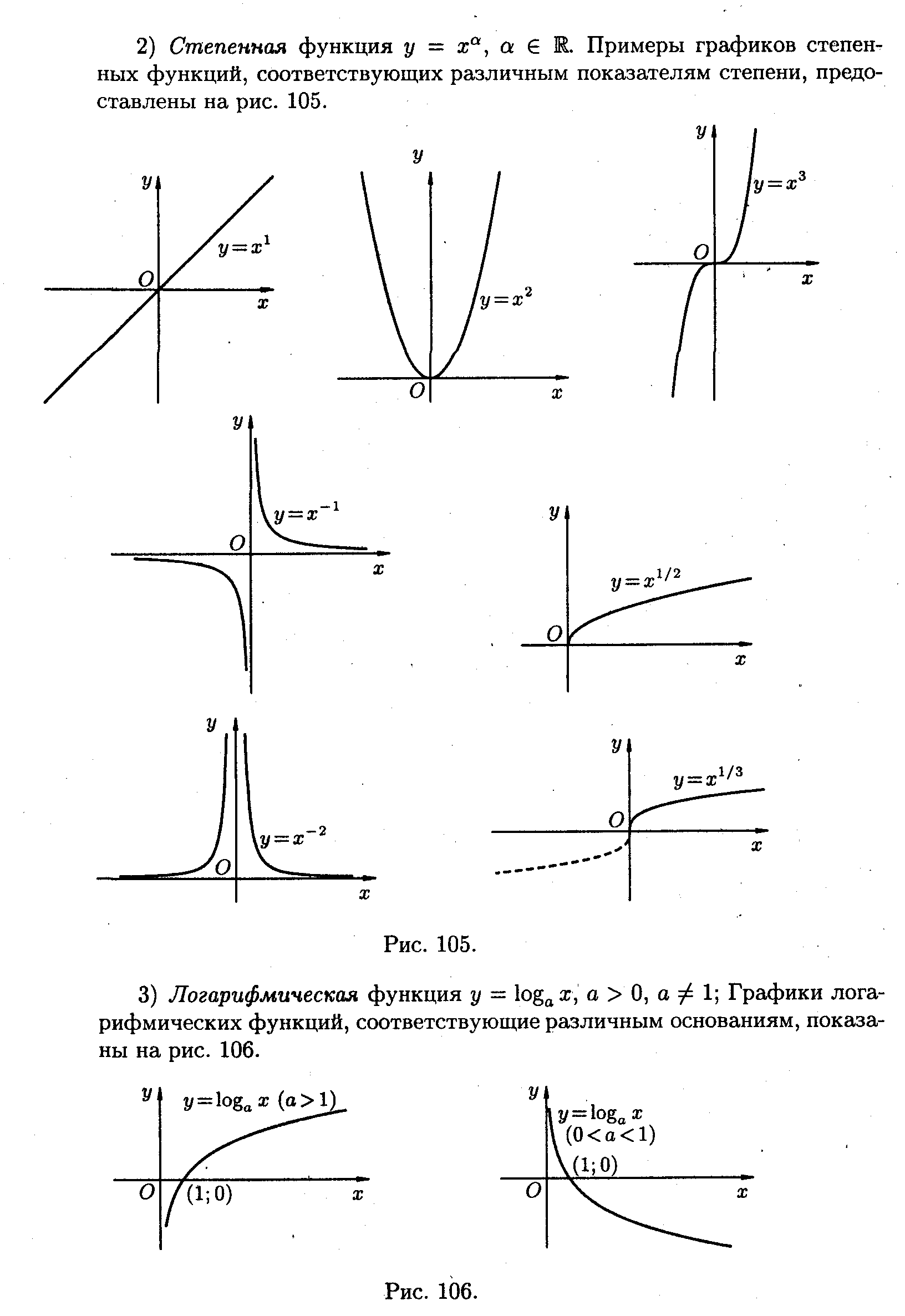
2. Степенева функція . Приклади графіків степеневих функцій, відповідних різним показникам степеня, надані на рис 105.

3) Логарифмічна функція . Графіки логарифмічних функцій, відповідні різним основам, показані на рис. 106

4 ) Тригонометричні функції y=sinx, y=cosx, y=tgx, y=ctgx. Графіки тригонометричних функцій мають вигляд, показаний на рис. 107.

5) Обернені тригонометричні функції . На рис. 108 показані графіки обернених тригонометричних функцій.

Функція, що задається однією формулою, складеною з основних елементарних функцій і постійних за допомогою скінченного числа арифметичних операцій (додавання, віднімання, множення, ділення) і операцій взяття функції від функції, називається елементарною функцією.

Прикладами елементарних функцій можуть служити функції

Прикладами неелементарних функцій можуть служити функції

Тема 5.3. Послідовності

5.3.1. Числова послідовність

Під числовою послідовністю _… розуміється функція

(15.1)

задана на множині натуральних чисел. Стисло послідовність позначається у вигляді або . Число називається першим членом (елементом) послідовності, - другим , -загальним або n-м членом послідовності.

Частіше всього послідовність задається формулою його загального виду члена. Формула (15.1) дозволяє обчислити будь-який член послідовності по номеру n, по ній можна відразу обчислити будь-який член послідовності.

Так, рівність

,

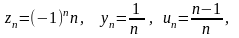
задають відповідно послідовності

=

Послідовність називається обмеженою, якщо існує таке число , що для будь-кого виконується нерівність

В окремому випадку послідовність називається необмеженою. Легко бачити, що послідовності і обмежені, а і – не обмежені.

Послідовність називається зростаючою (не спадною), якщо для будь-кого n виконується нерівність . Аналогічно визначається спадна (е зростаюча) послідовність. Всі ці послідовності називаються монотонними послідовностями . Послідовності , і монотонні, а - не монотонна.

Якщо всі елементи послідовності рівні одному і тому ж числу з, то її називають постійною.

Інший спосіб завдання числових послідовностей- рекурентний спосіб. В ньому задається початковий елемент (перший член послідовності) і правило визначення n-го елемента по (n-1)-му :

.

Таким чином, , 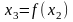і т.д. При такому способі задання послідовності для визначення 100-го члена треба спочатку порахувати всі 99 попередніх.