5.3.2. Границя числової послідовності

Можна помітити, що члени послідовності необмежено наближаються до числа 1. В цьому випадку говорять, що послідовність , прагне границі 1.

Число а називається границею послідовності , якщо для будь-якого додатного числа e знайдеться таке натуральне число , що при всіх виконується нерівність

(15.2)

В цьому випадку пишуть або і говорять, що послідовність (або змінна , пробігаюча послідовність , , ) має границю, рівну числу а (або прагне до а ). Говорять також, що послідовність наближається до а.

Коротко визначення границі можна записати так :

Приклад 15.1. Довести, що .

○ За означенням, число 1 буде границею послідовності

якщо знайдеться натуральне число , таке, що для всіх виконується нерівність, тобто . Воно справедливе для всіх , тобто для всіх = , де - ціла частина числа (ціла частина числа х, що позначається [x], є найбільше ціле число, не перевищує : [3]=3 [5,2]=5).

Якщо , то як можна узяти +1.

Отже вказано відповідне значення . Це і доводить, що

Звернемо увагу, що число залежить від .Так, якщо , то

якщо =0,01, то

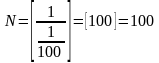
Тому іноді записують .

З'ясуємо геометричне значення означення границі послідовності.

Нерівність (15.2) рівносильна нерівностям - < -а < або a- < < a+ , які показують, що елемент знаходиться в - окіл точки а.

Тому означення границі послідовності геометрично можна сформулювати так : число а називається границею послідовності , якщо будь-яке - окіл точки а знайдеться натуральне число , що всі значення для яких , потраплять в -окіл точки а (див. рис.109).

Ясно, що чим менше e, тим більше число , але у будь-якому випадку всередині - окіл точки а знаходиться нескінченне число членів послідовності, а зовні неї може бути лише кінцеве їх число.

Звідси випливає, що послідовність, що збігається, має тільки одну границю. Послідовність, що не має границі, називається тією, що розходиться. Такий є, наприклад, послідовність (див. з рис. 107).

Постійна послідовність =c, n має границю, рівну числу 3, тобто . Дійсно, для при всіх натуральних n виконується нерівність (15.2). Маємо | -c|=|c-c|=0 < .

5.3.3. Граничний перехід в нерівностях

Розглянемо послідовності , і .

Теорема 15.1. Якщо =a, =b і починаючи з деякого номера виконується нерівність £ , то а £ b.

□ Припустимо, що a>b. З рівності =a і =b випливає, що знайдеться таке натуральне число ( ), що при всіх будуть виконаються нерівності | -a|< і | -b|< , тобто a- < <a+ і b- < <b+

Візьмемо . Тоді: >a- =a- = , тобто > і <b+ =b+ = , тобто < . Звідси випливає, що > _. Це суперечить умові £ . Отже, а £ b.■

Теорема 15.2. Якщо =a, =b і справедлива нерівність £ £

(починаючи з деякого номера), то 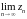=a.

(Без доведення)

5.3.4. Границя монотонної обмеженої послідовності. Число е. Натуральні логарифми.

Не всяка послідовність має границю. Сформулюємо без доведення ознаку існування границі послідовності.

Теорема 15.3 (Вейерштрасс). Всяка монотонна обмежена послідовність має границю.

Як приклад на застосування цієї ознаки розглянемо послідовність

= . По формулі бінома Ньютона

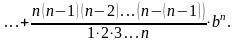
Покладем a=1, b= , отримаємо

або

(15.3)

З рівності (15.3) випливає, що із збільшенням n число додатних доданків в правій частині збільшується. Крім того, при збільшенні n число спадає, тому величини зростають. Тому послідовність зростаюча, при цьому

(15.4)

Покажемо, що вона обмежена. Замінимо кожну дужку в правій частині рівності (15.3) на одиницю; права частина збільшується, отримаємо нерівність

Підсилимо отриману нерівність, замінивши числа 3, 4, 5., що стоять в знаменниках дробів, числом 2 :

Тому

(15.5)

Отже, послідовність обмежена, при цьому для виконується нерівності (15.4) і (15.5) :

Отже, на підставі теореми Вейерштрасса послідовність

має границю, що позначається звичайно буквою е :

(15.6)

Число е називають неперовим числом. Число е ірраціональне, його наближене значення рівно 2,72 (е=2,718281828459045.). Число е прийнято за основу натуральних логарифмів : логарифм по підставі е називається натуральним логарифмом і позначається , тобто .

Знайдемо зв'язок між натуральним і десятковим логарифмами. За означенням логарифма маємо . Прологарифмуємо обидві частини рівності за основою10 :

, тобто

Користуючись десятковим логарифмом, знаходимо 0,4343. Значить, 0,4343 . З цієї формули випливає, що » , тобто »2,3026 . Отримані формули дають зв'язок між натуральними і десятковими логарифмами.