Тема 5.7. Неперервність функцій

5.7.1 Неперервність функцій у точці

Нехай функція визначена в точці ₀ і в деякому околі цієї точки. Функція називається неперервною в точці ₀, якщо існує границя функції в цій точці й вона дорівнює значенню функції в цій же точці, тобто

(19.1)

Рівність (19.1) передбачає виконання трьох умов:

1. функція визначена в точці ₀ і в її околі;

2. функція має границю при ₀ ;

3. границя функції в точці ₀ дорівнює значенню функції в цій точці, тобто виконується рівність (19.1).

Оскільки , то рівність (19.1) можна записати у вигляді:

(19.2)

Це означає, що при знаходженні границі неперервної функції можна перейти до границі під знаком функції , замість аргументу x підставивши його граничне значення ₀.

Наприклад, . У першій рівності функція й границя помінялись місцями (19.2) у силу неперервності функції e^x.

Приклад 19.1 Обчислити

○ при .●

Можна дати ще одне означення неперервності функції, опираючись на поняття приросту аргументу й функції.

Нехай функція визначена в деякому інтервалі (a;b). Візьмемо довільну точку ₀ (a;b) різниця x-x₀ називається приростом аргументу x в точці x₀ і позначається ∆x («дельта x »): ∆x= x-x- ₀.

Рис.119

Звідси x = ₀+∆x.

Різниця відповідних значень функцій ( ₀) називається приростом функції в точці ₀ і позначається ∆y (або ∆f або ∆f ( ₀)):

∆y= ( ₀) або ∆y=f( ₀+∆x)-f ( ₀).(див. рис.119 ).

Очевидно, що прирости ∆x і ∆y можуть бути як додатними, так і від’ємними числами.

Запишемо рівність (19.1) у нових позначеннях. За умови, що ₀ , то x-x₀ 0 однакові, і з (19.1) маємо:

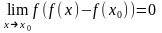або (19.3)

Отримана рівність (19.3) є ще одним визначенням неперервності функції в точці: функція називається неперервною в точці x₀ і її околі, якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції.

Досліджуючи неперервність функції в точці, застосовують або перше (рівність(19.1)), або друге (рівність(19.3)) визначення.

Приклад 19.2 Дослідити на неперервність функцію

○

Функція визначена для всіх x R. Візьмемо довільну точку x, надавши їй приросту ∆x, і знайдемо приріст ∆y:

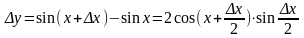
Тоді , тому що добуток обмеженої функції й н.м.ф.. Відповідно до означення (19.3), функція неперервна в точці x.

Аналогічно доводиться, що функція також неперервна. ●

5.7.2 Неперервність функції в інтервалі й на відрізку

Функція називається неперервною в інтервалі (a;b), якщо вона неперервна в кожній точці цього інтервалу.

Функція називається неперервною на відрізку [a;b], якщо вона неперервна в інтервалі (a;b); в точці неперервна праворуч (тобто ), а в точці 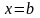неперервна ліворуч (тобто ).

5.7.3 Точка розриву і їх класифікація

Точки, у яких порушується неперервність функції, називаються точками розриву цієї функції. Якщо - точка розриву функції , то в ній не виконується принаймні одна з умов першого визначення неперервності функції, а саме:

1.Функція визначена в околі точки ₀ , але не визначена в самій точці ₀.

Рис. 120 рис.121

Наприклад, функція не визначена в точці ₀=2 (див. рис.120).

2. Функція визначена в точці ₀ і її околі, але не існує границі при ₀ .

Наприклад, функція

визначена в точці ₀=2 ( ), однак у точці ₀=2 має розрив (див. рис.121), тому що ця функція не має границі при :

, а

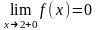
3. Функція визначена в точці ₀ і її околі, існує , але ця границя не дорівнює значенню функції в точці ₀:

Наприклад, функція (див.рис.122)

Рис. 122

Тут точка розриву:

, а

Всі точки розриву функції розділяються на точки розриву першого й другого роду. Точка розриву ₀ називається точкою розриву першого роду функції , якщо в цій точці існують границі функції ліворуч і праворуч (однобічні границі), тобто і . При цьому:

а) якщо А₁=А₂ , то точка ₀ називається точкою усувного розриву;

б) якщо А₁ А₂ , то точка ₀ називається точкою скінченого розриву.

Величину називають стрибком функції в точці розриву першого роду.

Точка розриву ₀ називається точкою розриву другого роду функції , якщо принаймні одна з односторонніх границь (ліворуч або праворуч) не існує або дорівнює нескінченності.

1. Звернемося до функцій, розглянутої вище (див. рис. 120).

, ₀=2 - точка розриву другого роду.

2. Для функції

, ₀=2 є точкою розриву першого роду,

скачок функції дорівнює .

3. Для функції

₀=0 є точкою усувного розриву першого роду.

Поклавши (замість ) при , розрив усунеться, функція стане неперервною.

Приклад 19.3. Дана функція . Знайти точки розриву, з'ясувати їхній тип.

○ Функція визначена й неперервна на всій числовій осі, крім точки . Очевидно, що . Отже, а .

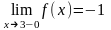Тому в точці функція має розрив першого роду.

Скачок функції в цій точці дорівнює 1-(-1)=2. ●