
- •Змістовий модуль 1 елементи лінійної алгебри
- •Основні поняття.
- •1.3.1. Основні поняття.
- •Основні поняття.
- •Тема 1.1 Матриці
- •1.1.1 Основні поняття
- •1.1.2. Дії над матрицями
- •Тема 1.2 Визначники
- •1.2.1. Основні поняття
- •1.2.2. Властивості визначників
- •Тема 1.3. Невироджені матриці
- •1.3.1. Основні поняття
- •1.3.2. Обернена матриця
- •1.3.3. Ранг матриці
- •Тема 1.4. Системи лінійних рівнянь.
- •Основні поняття
- •1.4.2 Розв'язок систем лінійних рівнянь. Теорема Кронекера – Капеллі.
- •1.4.3 Розв’язання невироджених лінійних систем. Формули Крамера.
- •1.4.4 Розв'язок систем лінійних рівнянь методом Гауса.
- •1.4.5 Системи лінійних однорідних рівнянь
Змістовий модуль 1 елементи лінійної алгебри
Тема 1.1 Матриці.
1.1.1. Основні поняття.
1.1.2. Дії над матрицями.
Тема 1.2. Визначники.
Основні поняття.
Властивості визначників.
Тема 1.3.Невироджені матриці.
1.3.1. Основні поняття.
Обернена матриця.
Ранг матриці.
Тема 1.4. Системи лінійних рівнянь.
Основні поняття.
Розв'язок системи лінійних рівнянь. Теорема Кронекера – Капеллі.
Розв’язання невироджених лінійних систем. Формули Крамера.
Розв’язання систем лінійних рівнянь методом Гауса.
Системи лінійних однорідних рівнянь .
Тема 1.1 Матриці
1.1.1 Основні поняття
Матрицею
називається
прямокутна таблиця чисел, що містить
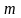 рядків
однакової довжини (або
рядків
однакової довжини (або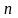 стовпців однакової довжини). Матриця
записується у виді
стовпців однакової довжини). Матриця
записується у виді

або,
скорочено,
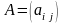 ,
де
,
де
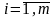 (тобто
(тобто
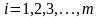 )
– номер рядка,
)
– номер рядка,
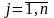 (тобто
(тобто
 )
– номер стовпця.
)
– номер стовпця.
Матрицю
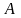 називають матрицею розміру
називають матрицею розміру
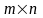 і
пишуть
і
пишуть
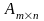 .
Числа
.
Числа
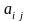 ,
що складають матрицю, називаються її
елементами.
Елементи, що стоять на діагоналі, що йде
з верхнього кута, утворюють головну
діагональ.
,
що складають матрицю, називаються її
елементами.
Елементи, що стоять на діагоналі, що йде
з верхнього кута, утворюють головну
діагональ.
Матриці рівні між собою, якщо рівні усі відповідні елементи цих матриць, тобто
 ,
якщо
,
якщо
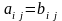 ,
де
,
.
,
де
,
.
Матриця,
у якої число рядків дорівнює числу
стовпців, називається квадратною.
Квадратну матрицю розміру
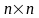 називають матрицею
-го
порядку.
називають матрицею
-го
порядку.
Квадратна матриця, у якої всі елементи, крім елементів головної діагоналі, дорівнюють нулеві, називається діагональною.
Діагональна
матриця, у якої кожен елемент головної
діагоналі дорівнює одиниці, називається
одиничною.
Позначається буквою
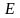 .
.
Приклад 1.1.1.
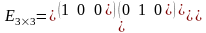
- одинична матриця 3-го порядку.
 .
.
- одинична матриця -го порядку.
Квадратна матриця називається трикутною, якщо всі елементи, розташовані по одну сторону від головної діагоналі, дорівнюють нулеві.
Матриця,
всі елементи якої дорівнюють нулеві,
називається нульовою.
Позначається
буквою
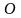 .
Має вигляд
.
Має вигляд
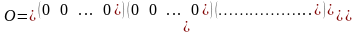 .
.
У матричному численні матриці і відіграють роль чисел 0 і 1 в арифметиці.
Матриця, що містить один стовпець або один рядок, називається вектором (або вектор-стовпець, або вектор-рядок відповідно). Їхній вигляд:
 ,
,
 .
.
Матриця
розміру
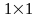 ,
що складає з одного числа, ототожнюється
з цим числом, тобто
,
що складає з одного числа, ототожнюється
з цим числом, тобто
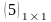 є 5.
є 5.
Матриця,
отримана з даної заміною кожного її
рядка стовпцем з тим же номером,
називається матрицею транспонованою
до
даної. Позначається
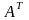 .
.
Так,
якщо
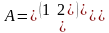 ,
те
,
те
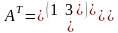 ,
якщо
,
якщо
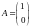 ,
те
,
те
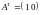 .
.
Транспонована
матриця має наступну властивість:
 .
.
1.1.2. Дії над матрицями
Додавання
Операція додавання матриць вводиться тільки для матриць однакових розмірів.
Сумою
двох матриць
 і
і
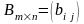 називається матриця
називається матриця
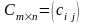 така, що
така, що
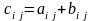
 .
.
Приклад 1.1.2.
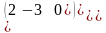 .
.
Аналогічно означається різниця матриць.
Множення на число
Добутком
матриці
 на число
на число
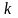 називається
матриця
така, що
називається
матриця
така, що
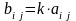 .
.
Приклад 1.1.3.
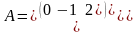 ,
,
 .
.
Матриця
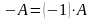 називається протилежною
матриці
.
називається протилежною
матриці
.
Різниця
матриць
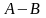 можна означити так:
можна означити так:
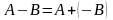 .
.
Операція додавання матриць і множення матриці на число мають наступні властивості:
1.
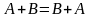 ;
;
2.
 ;
;
3.
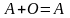 ;
;
4.
 ;
;
5.
 ;
;
6.
 ;
;
7.
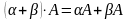 ;
;
8.
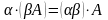 ,
,
де
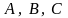 - матриці,
- матриці,
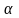 і
і
 - числа.
- числа.
Елементарні перетворення матриць
Елементарними перетвореннями матриць є:
перестановка місцями двох паралельних рядів матриці;
множення всіх елементів ряду матриці на число, відмінне від нуля;
додавання до всіх елементів ряду матриці відповідних елементів паралельного ряду, помноженого на одне і теж число.
Дві
матриці
і
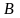 називаються еквівалентними,
якщо
одна з них виходить з іншої за допомогою
елементарних перетворень. Записується
називаються еквівалентними,
якщо
одна з них виходить з іншої за допомогою
елементарних перетворень. Записується
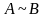 .
.
За допомогою елементарних перетворень будь-яку матрицю можна привести до матриці, у якої на початку головної діагоналі стоять підряд кілька одиниць, а всі інші елементи дорівнюють нулеві. Таку матрицю називають канонічною, наприклад
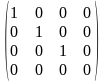 .
.
Приклад 1.1.4. Привести до канонічного виду матрицю
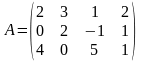 .
.
○ Виконуючи елементарні перетворення, одержуємо

 .
●
.
●
Добуток матриць
Операція множення двох матриць вводиться тільки для випадку, коли число стовпців першої матриці дорівнює числу рядків другої матриці.
Добутком
матриці
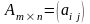 на матрицю
на матрицю
 називається матриця
називається матриця
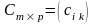 така, що
така, що
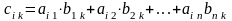 ,
де
,
де
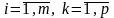 ,
,
тобто
елемент
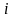 -й
рядка і
-го
стовпця матриці
на відповідні елементи
-го
стовпця матриці
.
-й
рядка і
-го
стовпця матриці
на відповідні елементи
-го
стовпця матриці
.
Одержання
елемента
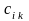 схематично зображується так:
схематично зображується так:


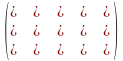 .
.
Якщо
матриці
і
квадратні одного розміру, то добутки
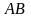 і
і
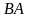 завжди
існують. Легко показати, що
завжди
існують. Легко показати, що
 ,
де
-
квадратна матриця,
- одинична матриця того ж розміру.
,
де
-
квадратна матриця,
- одинична матриця того ж розміру.
Приклад
1.1.5.

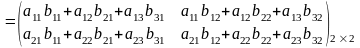 .
.
Приклад
1.1.6.
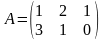 ,
,
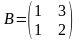 .
Тоді добуток
.
Тоді добуток
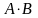 не визначений, тому що число стовпців
матриці
не визначений, тому що число стовпців
матриці
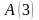 не збігається з числом рядків матриці
не збігається з числом рядків матриці
 .
При цьому обчислимо добуток
.
При цьому обчислимо добуток
 ,
який знаходять у такий спосіб:
,
який знаходять у такий спосіб:
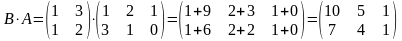 .
.
Матриці
і
називаються переставними,
якщо
 .
.
Множення матриць має наступні властивості:
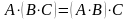 ;
;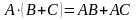 ;
;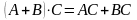 ;
;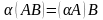 ,
,
якщо, звичайно, написані суми і добутки матриць мають сенс.
Для операції транспонування вірні властивості:
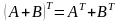 ;
;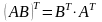 .
.
