Тема 1.4. Системи лінійних рівнянь.

1. Основні поняття

Системою лінійних алгебраїчних рівнянь, що містить рівнянь і невідомих, називається система вигляду

де числа називаються коефіцієнтами системи, числа - вільними членами. Підлягають знаходженню числа

Таку систему зручно записувати в компактній матричній формі .

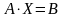Тут - матриця коефіцієнтів системи, називається основною матрицею:

,

- вектор - стовпчик з невідомих ,

- вектор - стовпчик з вільних членів .

Добуток матриць визначений, оскільки в матриці стовпців стільки ж, скільки рядків в матриці ( штук).

Розширеною матрицею системи називається матриця системи, що доповнена стовпцем вільних членів

Розв’язком системи називаються значень невідомих , при підстановці яких всі рівняння системи перетворюються в правильні рівності. Всякий розв'язок системи можна записати у вигляді матриці – стовпця .

Система рівнянь називається сумісною, якщо вона має хоча б один розв'язок, і несумісною, якщо вона не має жодного розв'язка.

Сумісна система називається визначеною, якщо вона має єдиний розв'язок, і невизначеною, якщо вона має більше одного розв'язку. В останньому випадку кожен її розв'язок називається частинним розв’язком системи. Сукупність усіх частинних розв’язків називається загальним розв’язком.

Розв’язати систему – це означає вияснити, сумісна вона чи несумісна. Якщо система сумісна, знайти її загальний розв'язок.

Дві системи називаються еквівалентними (рівносильними), якщо вони мають один і той же загальний розв'язок. Іншими словами, системи еквівалентні, якщо кожен розв'язок однієї з них є розв’язком для іншої, і навпаки.

Еквівалентні системи отримуються і при елементарних перетвореннях системи при умові, що перетворення виконуються лише над рядками матриці.

Система лінійних рівнянь називається однорідною, якщо всі вільні члени рівні нулю:

Однорідна система завжди сумісна, оскільки є розв’язком системи. Цей розв'язок називається нульовим або тривіальним.

1.4.2 Розв'язок систем лінійних рівнянь. Теорема Кронекера – Капеллі.

Нехай дана довільна система лінійних рівнянь з невідомими :

.

Вичерпну відповідь про сумісність цієї системи дає теорема Кронекера – Капеллі.

Теорема.1.4.1 Система лінійних алгебраїчних рівнянь сумісна тоді і лише тоді, коли ранг розширеної матриці системи дорівнює рангу основної матриці.

Приймемо без доведення.

Правила практичного пошуку всіх розв’язків сумісної системи лінійних рівнянь витікають з наступних теорем.

Теорема.1.4.2 Якщо ранг сумісної системи дорівнює числу невідомих, то система має єдиний розв'язок.

Теорема.1.4.3 Якщо ранг сумісної системи менший за число невідомих, то система має нескінченну множину розв’язків.

Правила розв'язку довільної системи лінійних рівнянь.

1. Знайти ранг основної і розширеної матриць системи. Якщо , то система несумісна.

2. Якщо система сумісна. Знайти якийсь базисний мінор порядку (нагадування: мінор, порядок якого визначає ранг матриці, називається базисним). Взяти рівнянь, з коефіцієнтів яких складається базисний мінор (інші рівняння відкинути). Невідомі, коефіцієнти яких входять в базисний мінор, називають головними і залишають ліворуч, а інші - невідомих називають вільними і переносять в праві частини рівнянь.

3. Знайти вираження головних невідомих через вільні невідомі. Отримано загальний розв'язок системи.

4. Надаючи вільним невідомим довільні значення, отримаємо відповідні значення головних невідомих. Таким чином можна знайти частинні розв'язки вихідної системи рівнянь.

Приклад 1.4.1. Дослідити на сумісність систему:

○ , , , .

Таким чином , тобто, система несумісна.●

Приклад 1.4.2. Розв’язати систему

○ . Беремо два перші рівняння:

.

Тобто, - спільний розв'язок. Поклавши, наприклад, , отримаємо один з частинних розв’язків : ●