Тема 1.3. Невироджені матриці

1.3.1. Основні поняття

Нехай - квадратна матриця -го порядку

.

Квадратна матриця називається невиродженою, якщо визначник не дорівнює нулеві: . У противному випадку матриця називається виродженою.

Матрицею, союзної до матриці , називається матриця

,

де - алгебраїчне доповнення елемента даної матриці (воно означається так само, як і алгебраїчне доповнення елемента визначника).

Матриця називається оберненою матриці , якщо виконується умова

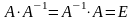(1.3.1)

де - одинична матриця того ж порядку, що і матриця . Матриця має ті ж розміри, що і матриця .

1.3.2. Обернена матриця

Теорема 1.3.1. Будь-яка не вироджена має обернену.

□ Проведемо доведення для випадку матриці 3-го порядку. Нехай

, причому .

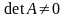Складемо союзну матрицю

і знайдемо добуток матриць і :

,

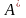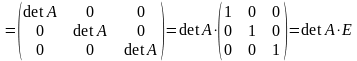т.п.

(1.3.2)

Тут ми використовували властивості 7 і 8 визначників (див. п. 1.2.2.).

Аналогічно переконуємося, що

. (1.3.3)

Рівності (1.3.2) і (1.3.3) перепишемо у виді

і

Порівнюючи отримані результати з визначенням (3.1), одержуємо

, тобто ■

Відзначимо властивості оберненої матриці:

1. ;

2. ;

3. .

Приклад 1.3.1. Знайти , якщо .

○ 1) Знаходимо .

2) Знаходимо , , , , тому .

3) Знаходимо : .

Перевірка:

. ●

Приклад 1.3.2. Визначити, при яких значеннях існує матриця, обернена до даної:

.

○Якщо , тобто , то , тобто матриця невироджена, має обернену. ●

Приклад 1.3.3. Показати, що матриця є оберненою для , якщо

, .

○ Знайдемо добуток матриць і :

Аналогічно . Отже, матриця є оберненою для .●

1.3.3. Ранг матриці

Розглянемо матрицю розміру .

.

Виділимо в ній рядків і стовпців . З елементів, що стоять на перетинанні виділених рядків і стовпців, складемо визначник -го порядку. Усі такі визначники називаються мінорами цієї матриці. У матриці пунктиром виділений мінор 2-го порядку. (Помітимо, що таких мінорів можна скласти штук, де - число сполучень з елементів по .)

Найбільший з порядків мінорів даної матриці, відмінних від нуля, називається рангом матриці. Позначається або .

Очевидно, що , де 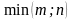- менше з чисел і .

Мінором, порядок якого визначає ранг матриці, називається базисним. У матриці може бути кілька базисних мінорів.

Приклад 1.3.4. знайти ранг матриці:

.

○ Усі мінори 3-го порядку дорівнюють нулеві. Є мінор 2-го порядку, відмінний від нуля . Виходить, . Базисний мінор стоїть на перетинанні 2 і 3 рядка з 1 і 3 стовпцем. ●

Відзначимо властивості рангу матриці:

1. При транспонуванні матриці її ранг не міняється.

2. Якщо викреслити з матриці нульовий ряд, то ранг матриці не зміниться.

3. Ранг матриці не змінюється при елементарних перетвореннях матриці (див. с. 12).

Ранг канонічної матриці дорівнює числу одиниць на головній діагоналі. На цьому заснований один зі способів обчислення рангу матриці.

Приклад 1.3.5. Знайти ранг матриці

,

використовуючи результати приклада 1.3.4.

○ У прикладі 1.3.4 показано, що

,

тобто

.

Таким чином, ранг матриці дорівнює .●