5.5.4. Ознаки існування границь

Не всяка функція, навіть обмежена, має границю. Наприклад, функція y=sinx при границі не має. В багатьох питаннях аналізу буває достатньо тільки переконатися в існуванні границі функції. В таких випадках користуються ознаками існування границь.

Теорема 17.10 (про границю проміжної функції). Якщо функція f(x) знаходиться між двома функціями j(х) і g(x), прямують до однієї і тієї ж границі, то вона також прямує цієї границі, тобто якщо

(17.6)

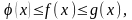(17.7)

□ З рівності (17.6) випливає, що для будь-кого існують два околи d₁ і d₂ точки , в одній з яких виконується нерівність

, тобто

(17.8)

а в іншій , тобто

. (17.9)

Нехай d-меньше з чисел d₁ і d₂. Тоді в d-окіл точки виконуються обидві нерівності (17.8) і (17.9).

З нерівностей (17.7) знаходимо, що

(17.10)

З врахуванням нерівностей (17.8) і (17.9) з нерівності (17.10) випливає нерівності або .

Ми довели, що

,

тобто .■

Теорему 17.10 іноді жартівливо називають «принципом двох міліціонерів». Роль «міліціонерів» грають функції j(x) і g(x), функція «слідує за міліціонерами».

Теорема 17.11 (про границю монотонної функції). Якщо функція f(x) монотонна і обмежена при x<x0 або x>x0, то існує відповідно її ліва границя або її права границя

Доведення цієї теореми не приводимо.

Наслідок 17.6. Обмежена монотонна послідовність , має границю.

5.5.5. Перша чудова границя

При обчисленні границь виразів, що містять тригонометричні функції, часто використовують границю

(17.11)

званий першою чудовою границею. Читається : границя відношення синуса до його аргументу рівна одиниці, коли аргумент прямує до нуля. Доведемо рівність (17.11).

В ізьмемо коло радіуса 1, позначимо радіану міру кута МОВ через х(див. рис. 113).

Нехай на рис. |AM|=sinx, дуга МВ чисельно рівна центральному куту х |BC|=tgx. Очевидно, маємо . На підставі відповідних формул геометрії одержуємо . Розділимо нерівності на, отримаємо або . Оскільки 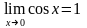і, то по ознаці (про границю проміжної функції) існування границь

. (17.12)

Нехай тепер . Маємо , де . Тому

. (17.13)

З рівності (17.12) і (17.13) випливає рівність (17.11).

Приклад 17.6. Знайти

○ Маємо невизначеність вигляду . Теорема про границю дробу незастосовна. Позначимо 3x=t; тоді при і , тому

●

Приклад 17.7. Знайти

○ ●

5.5.6. Друга чудова границя

Як відомо, границя числової послідовності, , має границю, рівній е (див.(15.6)) :

(17.14)

Доведемо, що числа е має і функція при (х є R) :

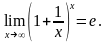(17.15)

1. Нехай Кожне значення х знаходиться між двома додатними цілими числами :, де - це ціла частина х. Звідси слідує

.

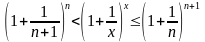Якщо , то . Тому, згідно (17.14), маємо :

За ознакою (про границю проміжної функції) існування границь

. (17.16)

1. Нехай . Зробимо підстановку , тоді

(17.17)

З рівності (17.16) і (17.17) випливає рівність (17.15).

Якщо в рівності (17.15) покласти ( 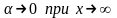), воно запишеться у вигляді

(17.18)

Рівність (17.15) і (17.18) називаються другою чудовою границею. Вони широко використовуються при обчисленні границь. В додатках аналізу велику роль грає показникова функція з підставою е. Функція y=xe називається експоненціальною, вживається також позначення ex=exp(x).

Приклад 17.8. Знайти

○ Позначимо x=2t, очевидно, t®¥ при . Маємо

●