
- •Змістовий модуль 5 вступ до математичного аналізу
- •Тема 5.1. Множини. Дійсні числа.
- •5.1.1. Основні поняття
- •5.1.2. Числові множини. Множина дійсних чисел
- •Тема 5.2. Функція
- •5.1.1. Поняття функції
- •5.2.2. Числові функції. Графік функції. Способи задання функцій
- •5.2.3. Основні характеристики функції
- •5.2.4. Обернена функція
- •5.2.5.Складна функція
- •5.2.6. Основні елементарні функції і їх графіки
- •Прикладами неелементарних функцій можуть служити функції
- •Тема 5.3. Послідовності
- •5.3.1. Числова послідовність
- •5.3.2. Границя числової послідовності
- •5.3.3. Граничний перехід в нерівностях
- •Тема 5.4. Границя функції
- •5.4.1. Границя функції в точці
- •5.4.2.Односторонні границі
- •5.4.3. Границя функції при х®¥
- •16.4.Нескінчено велика функція (н.В.Ф.)
- •Тема 5.5. Нескінченно малі функції (н. М. Ф.)
- •5.5.1. Означення і основні теореми.
- •5.2.2.Звязок між функцією, її границею і нескінченно малою функцією
- •5.5.3. Основні теореми про границі.
- •5.5.4. Ознаки існування границь
- •5.5.5. Перша чудова границя
- •5.5.6. Друга чудова границя
- •Тема 5.6.Еквівалентні нескінченно малі функції
- •5.6.1. Порівняння нескінченно малих функцій
- •5.6.2.Еквівалентні нескінченно малі і основні теореми про них
- •5.6.3.Застосування еквівалентних нескінченно малих функцій. Обчислення границь.
- •Тема 5.7. Неперервність функцій
- •5.7.4. Основні теореми про неперервні функції. Неперервність елементарних функцій
- •5.7.5 Властивості функцій, неперервних на відрізку
5.1.2. Числові множини. Множина дійсних чисел
Множини, елементами яких є числа, називаються числовими. Прикладами числових множин є :
 -
множина натуральних чисел;
-
множина натуральних чисел;
 ={
0 ;1;2; . ;
={
0 ;1;2; . ;
 ,.}-
множина цілих невід’ємних чисел;
,.}-
множина цілих невід’ємних чисел;
 ={0;
±1;
±2;
.; ±
;
.} –
множина цілих
чисел;
={0;
±1;
±2;
.; ±
;
.} –
множина цілих
чисел;
 ={
={
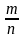 :
:

 ,
,
 }-
множина раціональних чисел.
}-
множина раціональних чисел.
 -
множина дійсних чисел.
-
множина дійсних чисел.
Між цими множинами існує співвідношення.

Множина
R
містить
раціональні і ірраціональні числа.
Всяке раціональне число виражається
або скінченним десятковим дробом або
нескінченним періодичним дробом. Так
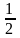 =0,5(=0,500.) =0,333. - раціональні числа.
=0,5(=0,500.) =0,333. - раціональні числа.
Дійсні числа, що не є раціональними, називаються ірраціональними.
Теорема 13.1. Не існує раціонального числа, квадрат якого рівний числу 2.
□ Припустимо, що існує раціональне число, представлене нескоротним дробом , квадрат якого рівний 2. Тоді маємо :
 =
2, тобто
=
2, тобто

Звідси
випливає, що
 (а
значить, і
)
– парне число, тобто
(а
значить, і
)
– парне число, тобто
 .
Підставивши
в
рівність
,
отримаємо
.
Підставивши
в
рівність
,
отримаємо
 ,
тобто
,
тобто
 .
Звідси
витікає, що число
–
парне,
тобто
.
Звідси
витікає, що число
–
парне,
тобто
 .
Але
тоді дріб дорівнює
скоротим
.
Але
тоді дріб дорівнює
скоротим
 .
Це суперечить припущенню, що дріб
скорочується. Отже, не існує раціонального
числа, квадрат якого рівний числу 2.
■
.
Це суперечить припущенню, що дріб
скорочується. Отже, не існує раціонального
числа, квадрат якого рівний числу 2.
■
Ірраціональне
число виражається нескінченним
неперіодичним дробом. Так
 =1,4142356..
p
= 3,14155926. - ірраціональні числа. Можна
сказати : множина дійсних чисел є множина
всіх нескінченних десяткових дробів.
І записати
=1,4142356..
p
= 3,14155926. - ірраціональні числа. Можна
сказати : множина дійсних чисел є множина
всіх нескінченних десяткових дробів.
І записати


Множина дійсних чисел володіє наступними властивостями.
Вона впорядкована
: для будь-яких двох різних чисел
 і
і
 має місце одне з двох співвідношень
має місце одне з двох співвідношень
 або
або
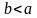 .
.
Множина
щільна
: між будь-якими двома різними числами
і
міститься
нескінченна множина дійсних чисел x,
тобто чисел, що задовольняють нерівності
 .
.
Так, якщо
,
то одним з них є число

 і
і

3.Множина
неперервна.
Нехай множина
розбита
на два непорожні класи
і
таких,
що кожне дійсне число міститься тільки
в одному класі і для кожної пари чисел
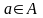 і
і
 виконано
нерівність
.
Тоді ( властивість неперервності) існує
єдине
виконано
нерівність
.
Тоді ( властивість неперервності) існує
єдине
 ,
яке задовольняє нерівності
,
яке задовольняє нерівності

 Воно
відділяє числа класу
від
чисел класу
.
Число
є
або найбільшим числом в класі
( тоді в класі
немає
якнайменшого числа ), або якнайменшим
числом в класі
( тоді в класі
немає
найбільшого ).
Воно
відділяє числа класу
від
чисел класу
.
Число
є
або найбільшим числом в класі
( тоді в класі
немає
якнайменшого числа ), або якнайменшим
числом в класі
( тоді в класі
немає
найбільшого ).
Властивість
неперервності дозволяє встановити
взаємно-однозначну відповідність між
множиною всіх дійсних чисел і множиною
всіх точок прямої. Це означає, що кожному
числу
 відповідає певна (
єдина ) точка числової осі і, навпаки,
кожній точці осі відповідає певне (
єдине ) дійсне число. Тому замість слова
« число» часто говорять « точка».
відповідає певна (
єдина ) точка числової осі і, навпаки,
кожній точці осі відповідає певне (
єдине ) дійсне число. Тому замість слова
« число» часто говорять « точка».
5.1.3. Числові проміжки. Окіл точки
Нехай і – дійсні числа, причому .
Числовими проміжками (інтервалами ) називають підмножини всіх дійсних чисел, що мають наступний вигляд :
 – відрізок (сегмент, замкнутий проміжок
);
– відрізок (сегмент, замкнутий проміжок
);
 – інтервал ( відкритий
проміжок );
– інтервал ( відкритий
проміжок );

 -
напіввідкриті інтервали ( або напіввідкриті
відрізки );
-
напіввідкриті інтервали ( або напіввідкриті
відрізки );

 ;
;

 ;
;
 –
нескінченні інтервали ( проміжки ).
–
нескінченні інтервали ( проміжки ).
Числа
і
називаються
відповідно лівим і правим кінцями
цих проміжків.
Символи
 і
і
 не числа, це символічне позначення
процесу необмеженого видалення точок
числової осі від початку 0 вліво і управо.
не числа, це символічне позначення
процесу необмеженого видалення точок
числової осі від початку 0 вліво і управо.
Н ехай
ехай
 –
будь-яке дійсне число (точки на числовій
прямій ). Околом
точки
називається будь-який інтервал
–
будь-яке дійсне число (точки на числовій
прямій ). Околом
точки
називається будь-який інтервал
 ,
що містить точку
.
Зокрема, інтервал
,
що містить точку
.
Зокрема, інтервал
 ,
де
,
де
 ,
називається
-
околом точки
.
Число
називається центром,
а число
-
радіусом.
,
називається
-
околом точки
.
Число
називається центром,
а число
-
радіусом.
рис. 97
Якщо
 ,
то виконується нерівність
,
то виконується нерівність
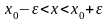 ,
або, що те ж
,
або, що те ж
 .
Виконання останньої нерівності означає
попадання точки
в
-околі
точки
.(див.
рис. 97)
.
Виконання останньої нерівності означає
попадання точки
в
-околі
точки
.(див.
рис. 97)
