1.2. Теорема про множини, гомеоморфні множині Кантора

Завданням цього підрозділу є доведення того факту, що будь-яку компактну, досконалу і цілком незв’язну множину можна неперервно перетворити в пил Кантора, причому існує обернене перетворення, з допомогою якого можна відновити вихідну множину. Тобто потрібно довести, що властивість бути Канторовою множиною є топологічною інваріантою.

Ми вже показали, що класичний пил Кантора має властивості компактності, неперервності та цілковитої незв’язності, отож залишилося лише нагадати означення неперервного відображенння та дати пояснення терміну „топологічні інваріанти” [8:300].

1.2.1. Н е п е р е р в н і в і д о б р а ж е н н я т а і н в а р і а н т и

н е п е р е р в н о с т і.

Означення 1.3. Нехай функція визначена на підмножині 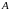простору і приймає значення в . Кажуть, що неперервна в точці , якщо

,

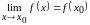тобто для кожного існує таке число , що з , слідує .

Іншими словами, функція неперервна в точці , якщо для кожної послідовності , що збігається до , існує границя

. (1.1)

Означення 1.4. Відображення називається неперервним на , або просто неперервним, якщо неперервна у всіх точках .

У загальному випадку функція ставить у відповідність елементам одного метричного простору елементи іншого метричного простору .

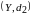Нас цікавлять властивості вихідної множини , які при неперервному відображенні зберігаються без змін у множини . Такі властивості будемо називати інваріантами неперервності.

Означення 1.5. Множина в називається відносно відкритою в , якщо можна вказати таку відкриту множину в , що . Відповідно, називається відносно замкненою в , якщо можна вказати таку замкнену множину в , що .

Наприклад, напіввідкритий інтервал є відносно відкритим у множині . Відносно замкненою множиною в є напіввідкритий інтервал .

Нехай – підмножина області значень . Прообразом при відображенні називається множина

.

Наприклад, якщо то .

Перед тим, як перейти до основної теореми цього розділу, спочатку виведемо ряд важливих підтеорем, котрі потім ефективно зможемо використати при доведенні інваріантності множини Кантора.

Теорема 1.1. Відображення з на неперервне тоді і тільки тоді, якщо прообраз кожної множини , відносно відкритої (відносно замкненої) в 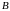, відносно відкрита (відносно замкнена) в .

Доведення. (Випадок відносно відкритих множин.)

Достатність. Нехай і . Множина , відносно відкрита в . Так як за умовою відносно відкрита в , то існує така відкрита множина в , що . Виберемо так, щоб . Тоді . А отже, відображення неперервне.

Необхідність. Нехай і . Так як множина відносно відкрита в , то існує така відкрита множина в , що . Виберемо так, щоб . Тоді для деякого , внаслідок неперервності в точці . Визначимо відкриту множину в як об’єднання куль 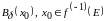. Тоді , і тому . А отже, відносно відкрита в . Доведено.

Доведення цієї теореми дає нам важливі наслідки.

Наслідок 1. Нехай і _– відкриті множини. Відображення неперервне тоді і тільки тоді, якщо прообраз кожної відкритої множини відкритий.

Доведення. Так як відкрита, а відносно відкрита в , то відкрита в . За теоремою 1.1 для неперервності необхідно, щоб прообраз кожної множини був відносно відкритий в . Оскільки сама відкрита, то достатньо вимагати відкритості в . Доведено.

Наслідок 2. Нехай і _– замкнені множини. Відображення неперервне тоді і тільки тоді, якщо прообраз кожної замкненої множини замкнений.

Доведення. Так як замкнена, а відносно замкнена в , то замкнена в . За теоремою 1.1 для неперервності необхідно, щоб прообраз кожної множини був відносно замкнений в . Оскільки сама замкнена, то достатньо вимагати замкненості в . Доведено.

Далі покажемо, що наша множина С при неперервному відображенні f відобразиться в компактну множину. При доведенні розглянемо загальний випадок.

Теорема 1.2. Нехай - компактна підмножина . Якщо відображення неперервне, то множина компактна.

Доведення. В загальному випадку, множина є компактною, якщо з кожної послідовності точок можна виділити підпослідовність, що збігається до деякої точки даної множини. Нехай – послідовність з , а – послідовність з , причому

. Так як компактна, то з послідовності можна виділити підпослідовність , що збігається до деякої точки . З умови (1.1) слідує:

(1.2) Таким чином, підпослідовність 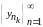з збігається до точки з . Доведено.

Теорема 1.3. Нехай - зв’язна підмножина . Якщо відображення неперервне, то множина зв’язна.

Доведення. По-перше, відмітимо, що множина зв’язна тоді і тільки тоді, коли вона не є об’єднанням двох непорожніх неперерізних відносно відкритих в множин.

Припустимо, що множина незв’язна. Тоді , де і _– непорожні неперерізні відносно відкриті в множини. За наслідком 1, множини і відносно відкриті в і не перетинаються, а тому множина не є зв’язною, що суперечить умові. Доведено.

1.2.2. Т о п о л о г і ч н і і н в а р і а н т и. Дамо означення топологічної інваріантності. Якщо функція відображає на взаємно однозначно, то існує обернена функція :

, де . Наприклад, функція відображає дійсну пряму на взаємно однозначно. Оберненою функцією для неї є . В загальному випадку обернена функція може бути і розривною, навіть якщо функція неперервна. Однак, якщо компактна, то функція неперервна.

Означення 1.6. Взаємно однозначна неперервна функція, що має неперервну обернену, називається гомеоморфізмом або топологічним відображенням.

В цьому випадку множини і називаються гомеоморфними або топологічно еквівалентними. Властивості множин, які зберігаються при гомеоморфізмі, називаються топологічними інваріантами. Двома такими властивостями є компактність і зв’язність. Тут варто згадати також повну незв’язність та досконалість множин.

Наступна теорема дає можливість показати, що взаємно однозначне неперервне відображення компакту є гомеоморфізм. Оскільки множина С є компактною множиною, то дане доведення відноситься до неї безпосередньо і може бути використане нами при доведенні основної теореми.

Теорема 1.4. Якщо є взаємно однозначне неперервне відображення компакту на , то обернена функція також неперервна, тобто є гомеоморфізмом.

Доведення. За наслідком 2 з теореми 1.1, достатньо показати, що образ кожної замкненої множини замкнений. Нехай та при . Доведемо, що . Так як компактна, то існує підпослідовність і така точка , що . Так як замкнена, то отримаємо , і внаслідок неперервності , . З цього випливає, що , і тому . Доведено.

1.2.3. О с н о в н а т е о р е м а

Властивість бути канторовою множиною є топологічним інваріантом. Це означає, що якщо A гомеоморфна B, причому A – компактна, досконала і цілком незв’язна, то B також компактна, досконала і цілком незв’язна.

Доведення. Нехай f – гомеоморфізм із A на B. Так як множина A – компактна, а відображення f неперервне, то по теоремі 1.2 множина B = f(А) також компактна.

Згідно з теоремою 1.3, зв’язність є топологічним інваріантом. Якщо C – компонента f(B), то f (C) є зв’язна множина в A. Так як A – цілком незв’язна, то її складовими є окремі точки. Таким чином, C повинна бути окремою точкою. Звідси слідує, що B також незв’язна.

Так як A досконала, то A замкнена і не має ізольованих точок. Оскільки B компактна, то вона є замкненою. Припустимо, що y = f (x) – ізольована точка B. Тобто існує множина U, відносно відкрита в B, яка не містить ніяких інших точок з B, крім у. Але тоді f (U) буде відносно відкритою множиною в A і не міститиме ніяких інших точок з A, крім x, щo призводить до протиріччя умові (множина A – досконала). Отже множина B не має ізольованих точок, а тому вона досконала. Доведено.

Зауваження 1. Очевидно, що всі наведені вище приклади множин є об'єктами, гомеоморфними класичному пилу Кантора.

Зауваження 2. Топологічні відображення (гомеоморфізми) не зберігають метричних властивостей множин. Для наочності цього факту уявимо фрактал, що намальований на гумовій стрічці, котра потім нерівномірно розтягується в різних напрямках. Отримана фігура гомеоморфна оригіналові, але такі властивості, як самоподібність і фрактальна розмірність не зберігаються.