
- •Класичні фрактали
- •4.4. Завдання……………………………………………………...115
- •Множина Кантора
- •1.1 Фрактал Кантора
- •1.1.4. В е к т о р н а (арифметична) с у м а м н о ж и н к а н т о р а.
- •1.2. Теорема про множини, гомеоморфні множині Кантора
- •1.3. Застосування множин, гомеоморфних множині Кантора
- •1.4. Завдання
- •Cніжинка Коха
- •2.1. Означення сніжинки Коха
- •2.2. Властивості сніжинки Коха
- •2.3. Острівець Коха та його властивості
- •2.4. Мавпяче дерево
- •2.5. Узагальнення сніжинки Коха
- •2.6. Дослідження аналогів зірки Коха у тривимірному просторі
- •Брунькова модель,
- •Каркас брунькової моделі.
- •2.7. Кубічне узагальнення сніжинки Коха
- •2.8. Завдання
- •3.1. Килим та цвинтар Серпінського
- •3.2. Двовимірне узагальнення килима Серпінського
- •3.3. Аналоги килима Серпінського в тривимірному просторі
- •3.4. Тривимірні узагальнення килима Серпінського
- •3.5. Чотиривимірні аналоги килима Серпінського
- •3.6. Трикутний килим Серпінського, його властивості та способи задання
- •3.7. Узагальнення серветки Серпінського
- •Трикутник Паскаля за
- •3.8. Завдання
- •Крива Пеано
- •4.1. Побудова кривої Пеано
- •4.2. Відомі різновиди та узагальнення кривої Пеано
- •4.3. Узагальнення кривої Пеано на чотиривимірний та п’ятивимірний простори
- •4 Мал.2 .3.2. Узагальнення кривої Пеано на п’ятивимірний простір.
- •4.3.3. Узагальнення кривої Пеано на п-вимірний простір.
- •4.4. Завдання
Множина Кантора
Структури,
які ми будемо розглядати в цьому розділі,
утворені точками на прямій, тому їх
порівняно легко досліджувати. Крім
того, з їх допомогою можна в найбільш
доступній формі представити деякі
поняття, що займають центральне місце
в теорії фракталів, але настільки рідко
застосовувалися у минулому, що для їх
позначення не було навіть придумано
термінів. Почнемо з терміну “пил”, який
відтепер набуває спеціальне значення
як неформальний еквівалент терміну
“множина, топологічна розмірність
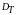 якої рівна 0” (так само, як “крива” і
“площина” означають множини, топологічна
розмірність яких рівна, відповідно, 1 і
2).
якої рівна 0” (так само, як “крива” і
“площина” означають множини, топологічна
розмірність яких рівна, відповідно, 1 і
2).
1.1 Фрактал Кантора
Класична множина Кантора, або пил Кантора, була названа на честь Георга Кантора, який описав її в 1883 році. Існування пилу Кантора відмічалось ще в 1875 році Генрі Смітом. Ця множина добре відома як приклад Лебегової множини міри нуль, потужність якої рівна потужності континуума [0,1]. Фрактальні властивості пилу Кантора мають надзвичайно важливе значення, особливо враховуючи той факт, що багато відомих фракталів є її близькими „родичами” [8:38].
1.1.1. П о б у д о в а т а в л а с т и в о с т і.
Побудова пилу Кантора. Побудова класичного пилу Кантора починається з викидання середньої третини (не включаючи кінці) одиничного відрізку. Тобто вихідною множиною є відрізок [1, 0], і перший крок полягає в тому, що ми викидаємо відкритий інтервал (1/3, 2/3). На наступному і всіх інших етапах ми викидаємо середню третину (не включаючи кінці) всіх відрізків на даному рівні. Таким чином ми отримуємо (рис. 1.1) послідовність множин [8:39]:
С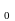 =[0,1]
=[0,1]
С =[0,1/3]
=[0,1/3] [2/3,1]
[2/3,1]
С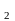 =[0,1/9]
[2/9,1/3]
[2/3,7/9]
[8/9,1]
=[0,1/9]
[2/9,1/3]
[2/3,7/9]
[8/9,1]
С.
Гранична
множина С, що являє собою перетин множин
С ,
n
= 0, …,i
називається класичним пилом Кантора.
,
n
= 0, …,i
називається класичним пилом Кантора.
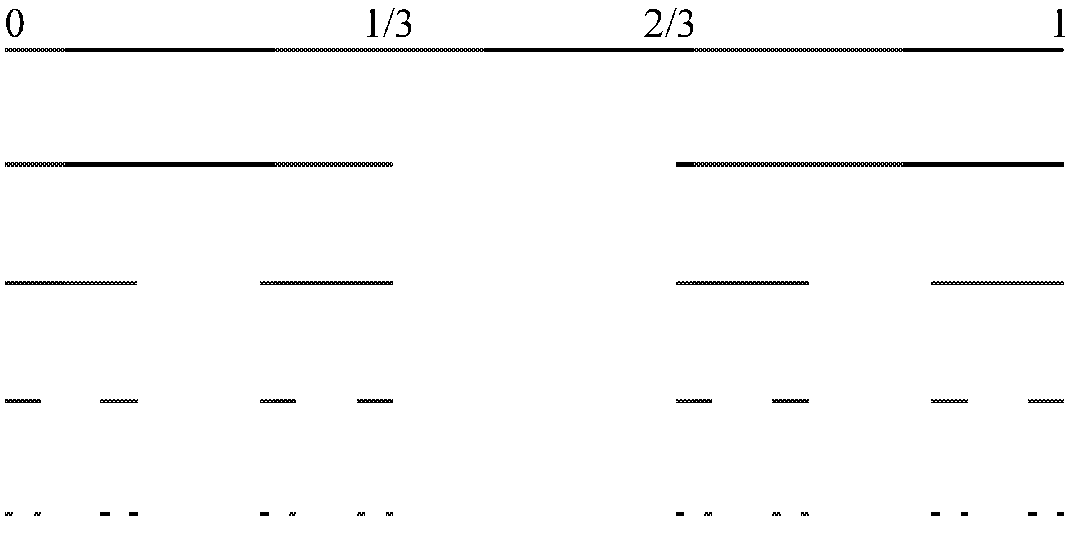
Рис. 1.1.
Канторів гребінь. Оскільки показати графічно пил Кантора надзвичайно важко в силу його розрідженості, то для наочності частіше використовують зображення (рис. 1.2), що є декартовим добутком множини С на відрізок якоїсь довжини. В даному випадку – на відрізок [0, 3]. В такому вигляді множина Кантора носить назву Канторового гребня.
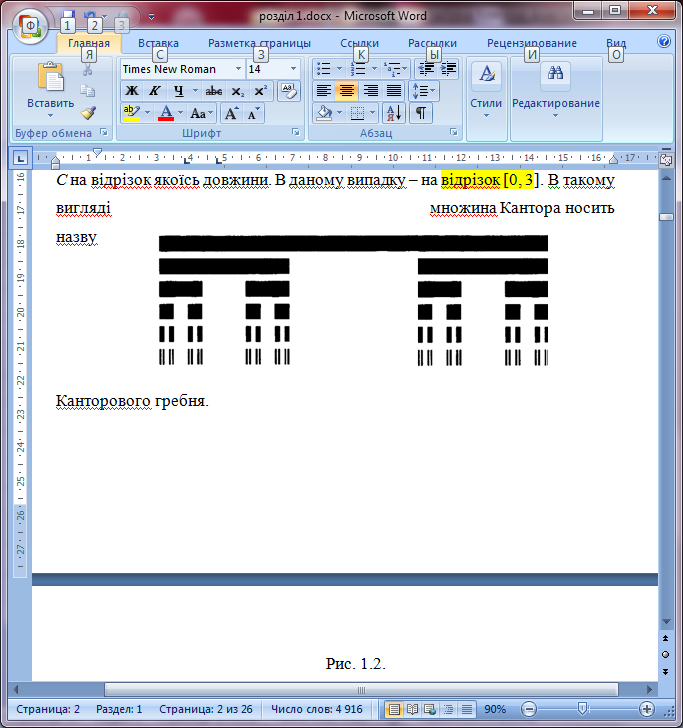
Рис. 1.2.
Властивості пилу Кантора
Властивість 1. Канторів пил не містить інтервалів додатної довжини.
Це, в свою чергу, означає, що сума довжин інтервалів, які викидаються при побудові дорівнює 1.
Доведення. Довжина першого інтервалу, який ми викинули складає 1/3. Щоб отримати С2, ми викинули два інтервали, кожний довжини 1/(32). На наступному кроці ми викинули 22 інтервалів, кожний довжини 1/33 і т.д. Таким чином сума довжин викинутих інтервалів S складає:
S = 1/3 + 2/32 + 22/33 + … + 2n-1/3n + …
Перепишемо цей вираз у вигляді:
S = (1/3)(1+2/3+(2/3)2+(2/3)3+…), і за допомогою формули суми геометричної прогресії, а саме
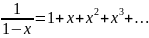 ,
де
,
де
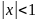
ми отримуємо
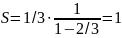
Це означає, що сума довжин сегментів, що залишилися має бути рівна 0. Доведено.
Властивість 2. Потужність множини Кантора С дорівнює потужності континууму.
Доведення. Дві множини мають однакову (рівну) потужність, якщо існує взаємно однозначна відповідність між точками цих множин.
Нам потрібно встановити взаємно однозначну відповідність між точками із С і точками відрізку [0, 1]. Для цього проведемо дослідження арифметичної структури множини Кантора. Розглянемо двійковий (по основі два) і трійковий (по основі три) розклади точок відрізку [0, 1].
Для того, щоб уникнути непорозумінь в тому випадку, коли точка має два двійкові чи трійкові представлення, ми будемо завжди вибирати те представлення яке закінчується всіма одиницями в двійковому розкладі і всіма двійками в трійковому.
Відмітимо, що точка попадає в множину Кантора С тоді і тільки тоді, коли в її трійковому представленні відсутні одиниці, тобто коли в ньому присутні тільки нулі або двійки.
Тобто,
множина С –
це множина всіх точок відрізка[0,
1], які можуть
бути записані трійковим дробом
 без вживання цифри 1:
без вживання цифри 1:
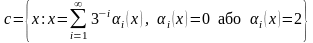 .
.
Тоді шукана відповідність точок із С з точками відрізку [0,1] здійснюється заміною всіх двійок в трійковому представленні х на 1. Двійкове представлення отримане таким чином, визначає деяке дійсне число у. Наприклад, якщо х належить С є:
х=0,0022002200202...(в трійковій системі),
то покладаємо
у=0,0011001100101...(в двійковій системі).
Описана процедура визначає взаємно однозначну відповідність між х С і у [0,1]. Це і доводить континуальність С. Доведено.
Властивість 3. Множина Кантора вимірна за Лебегом і її лебегова міра рівна 0.
Доведення.
Нагадаємо, що множина С
називається вимірною за Лебегом, якщо
m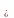 С=m
С=m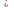 С,
а спільне значення m
С
і m
С
називається мірою Лебега множини С
і позначається mС:
С,
а спільне значення m
С
і m
С
називається мірою Лебега множини С
і позначається mС:
mС = m С=m С,
де m С – зовнішня міра Лебега обмеженої множини точок С [a;b], тобто (за означенням зовнішньої міри) нижня межа сум довжин усіх можливих скінченних або зчисленних попарно неперекривних інтервалів Сk, які покривають множину С і містяться на сегменті [a;b]:
m
С=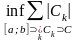 ,
,
де Сk - довжина інтервалу Сk., a m C – внутрішня міра множини C [a;b] за Лебегом, тобто (за означенням внутрішньої міри) це число
m C=(b-a)- m CC,
де CC=[a;b]\C – доповнення множини C до [a;b].
Перейдемо до множини Кантора:
m С=0, оскільки сума довжин сегментів Сk рівна 0, що було показано вище;
m С=(1-0)-m CС=(1-0)-1=0, оскільки доповненням множини С до відрізку [0, 1] є об’єднання всіх викинутих інтервалів, сума довжин яких рівна 1. Ми отримали наступний результат:
m С=m С=0.
Тобто, множина Кантора вимірна за Лебегом і її лебегова міра рівна 0. Доведено.
Властивість 4. Замкненість.
Доведення. Множина називається замкненою, якщо вона містить у собі всі свої граничні точки, тобто С С.
Назвемо
замкненими відрізками першого рангу
ті два замкнені відрізки, які залишаються
на площині після викидання центрального
інтервалу, а сам центральний
інтервал – відкритим інтервалом першого
рангу. Аналогічно визначимо замкнені
інтервали другого рангу (їх кількість
дорівнює 22)
і відкриті інтервали другого рангу.
Продовжуючи таким чином ми визначимо
відкриті і замкнені множини всіх рангів.
Ясно, що С=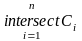 ,
де Сn
– об’єднання всіх замкнених множин
рангу n.
Так як кожна множина Сi,
i=1,
2, …,n
замкнена, то і їх перетин (тобто С)
також замкнений. Доведено.
,
де Сn
– об’єднання всіх замкнених множин
рангу n.
Так як кожна множина Сi,
i=1,
2, …,n
замкнена, то і їх перетин (тобто С)
також замкнений. Доведено.
Властивість 5. Множина С – ніде не щільна.
Доведення.
Щоб довести, що С
ніде не щільна розглянемо довільний
відкритий інтервал J.
Цей інтервал або повністю вільний від
точок множини С,
або містить хоча б одну його точку М.
Доведемо, що в останньому випадку в J
знайдеться менший інтервал, повністю
вільний від точок множини С.
Для того, щоб переконатися в цьому
розглянемо замкнений відрізок Сn
рангу n,
що містить М
і такий, щоб його довжина була менша
відстані від точки М
до границі J
(це можливо здійснити, так як довжини
замкнених Сk
прямують до нуля при n→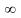 ).
Цей відрізок повністю лежить всередині
J.
Тоді відкритий інтервал n+1-го
рангу, що лежить всередині відрізка Сn,
повністю вільний від точок множини С
(і також лежить всередині інтервалу
J).
Звідси
слідує, що інтервал, вкладений в цей
відрізок, буде лежати всередині інтервалу
J
і не буде містити точок множини С.
Отже, С
– ніде не щільна множина на площині.
Доведено.
).
Цей відрізок повністю лежить всередині
J.
Тоді відкритий інтервал n+1-го
рангу, що лежить всередині відрізка Сn,
повністю вільний від точок множини С
(і також лежить всередині інтервалу
J).
Звідси
слідує, що інтервал, вкладений в цей
відрізок, буде лежати всередині інтервалу
J
і не буде містити точок множини С.
Отже, С
– ніде не щільна множина на площині.
Доведено.
Властивість 6. Досконалість.
Доведення. Множина називається досконалою, якщо вона замкнена і не містить ізольованих точок. Точка х множини А називається ізольованою точкою цієї множини, якщо вона міститься в околі, що не містить інших точок цієї множини.
Покажемо, що С не має ізольованих точок. Нехай М0 належить С; опишемо навколо М0 довільний окіл J і розглянемо замкнений сегмент Сn, що містить М0 і міститься в J. Межі цього сегменту будуть належати С і міститися в J. Отже, М0 не є ізольованою точкою.
Так як С замкнена і не містить ізольованих точок, то С – досконала множина. Доведено.
Властивість 7. Компактність.
Доведення.
Нагадаємо,
що множина А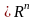 називається компактною, якщо вона
замкнена і обмежена; множина А
називається обмеженою, якщо вона має
скінченний діаметр. Тобто:
називається компактною, якщо вона
замкнена і обмежена; множина А
називається обмеженою, якщо вона має
скінченний діаметр. Тобто:
 (А)<
;
діаметром множини
А
називається наступна величина:
(А)<
;
діаметром множини
А
називається наступна величина:
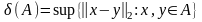 .
.
Для того, щоб показати, що множина Кантора компактна, переконаємося в тому, що вона замкнена і обмежена. Замкненість множини С було доведено вище. Обмеженість очевидна (вся множина цілком міститься на сегменті [0, 1]). Приходимо до висновку, що множина С – компактна. Доведено.
Властивість 8. Множина Кантора C – цілком незв’язна.
Говорять, що множина А – цілком незв’язна, якщо найбільші зв’язні підмножини множини А являють собою одноточкові множини, іншими словами, якщо всі компоненти А – одиночні точки. Так як множина Кантора є об’єднанням відрізків Ск, сума довжин яких, як було доведено вище, рівна нулю, то всі Ск – одиночні точки. Доведено.
Означення
1.1. Фігура А
– самоподібна, якщо
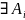 А,
якщо виконуються умови
А,
якщо виконуються умови
1)
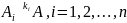
2)
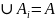
3)
 – «малий» (
– «малий» (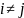 ),
де
),
де
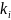 –
коефіцієнт подібності,
–
коефіцієнт подібності,
 .
.
Означення
1.2. Розмірністю само подібності множини
А
є корінь рівняння
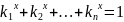 ,
де
–
коефіцієнт подібності,
.
,
де
–
коефіцієнт подібності,
.
Властивість 9. Пил Кантора є самоподібний фрактал розмірності D=log(2)/log(3)≈0,6309.
Доведення. Виведення цієї властивості очевидно слідує з самого означення розмірності самоподібності. Доведено.
Наведемо кілька прикладів множин типу Кантора [8:43].
Приклад 1. Множина Кантора розмірності D≈0,9542.
Позначимо через х множину всіх дійсних чисел відрізку [0,1], в десятковому представленні яких:
х=0,х1х2х3...
відсутня якась цифра, наприклад цифра сім. Так, числа
0=0,000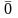 ...
...
1=0,99999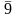 ...
...
¼=0,2500 ...
належать множині Х. Належить Х і число 0,7, так як ми можемо записати його наступним чином:
0,7=0,6999 ...,
тобто не використовуючи цифру 7.
По деяким міркуванням стає зрозуміло, як побудувати множину Х. Нехай Х0 = [0, 1]. Розділимо Х0 на десять рівних інтервалів. Цифра х1 вказує, якому з інтервалів належить х. Якщо х1 = 0, то х попадає в перший інтервал і т.д. Але є випадок, коли х співпадає з кінцем якогось відрізка. Тоді маємо два можливих представлення числа х: одне закінчується всіма нулями, інше – всіма дев’ятками. Але це не складає жодних проблем, оскільки ми домовились наперед, що жодна цифра хі не дорівнює 7. Оскільки х1 ≠ 7, то х не попадає в восьмий інтервал, тобто х (0,7;0,8). Викинемо цей інтервал і позначену множину, що залишилась через х1. Розділимо кожний із дев’яти інтервалів, що залишились, на десять рівних частин. Так як х2 ≠ 7, то ми можемо викинути кожний восьмий із отриманих інтервалів. Позначимо нову множину через Х2. Повторюючи цю процедуру нескінченне число раз, отримаємо послідовність вкладених множин Х0 ,Х1, Х2,... Шукана множина Х є перетином всіх цих множин. Із побудови слідує, що Х представляє собою об’єднання N=9 зменшених в 10 раз (r=1/10) копій самого себе. Таким чином Х – самоподібний фрактал, і його фрактальна розмірність рівна D=log(9)/log(10)≈0,9542.
Приклад 2. Множина Кантора розмірності D = 1.
Перейшовши від прямої до площини, можна побудувати множину Кантора розмірності D=1. Нехай початкова множина одиничний квадрат на площині з вершинами в точках (0,0), (1,0), (1,1), (0,1). На кожному кроці квадрати замінюються чотирма меншими як показано на рисунку 1.3. Гранична множина цієї побудови є самоподібний фрактал із N=4 і коефіцієнтом подібності r=1/4. Звідси слідує, що його розмірність рівна:
D = log(4)/log(4) = 1.
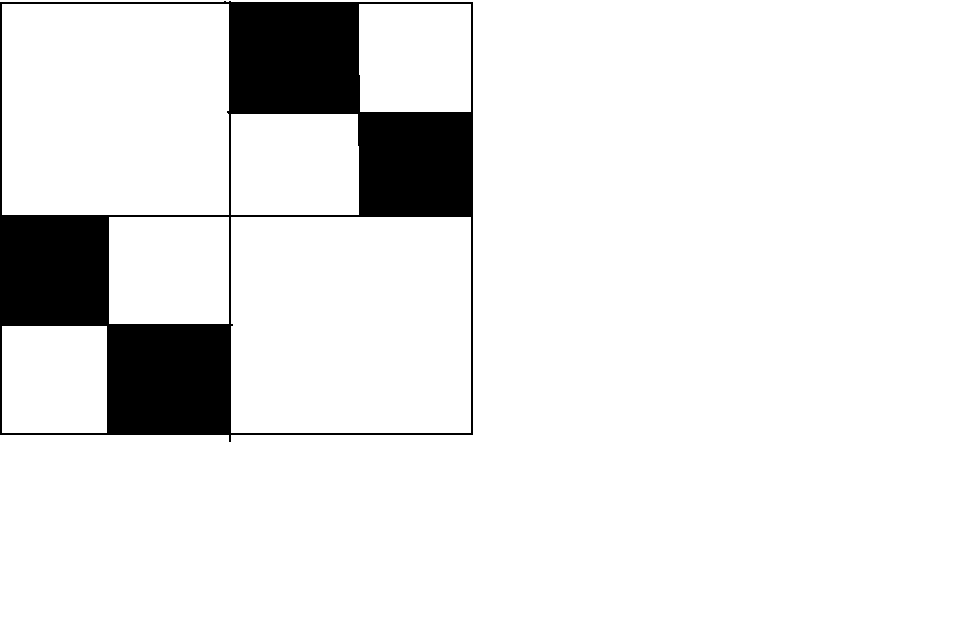
Рис. 1.3.
Далі розглянемо множину Кантора дещо детальніше з алгебраїчної точки зору.
1.1.2.
Ч о р т о в а д р а б и н а. Існує
функціональний аналог множини Кантора
– функція Кантора [21]. Вона будується
наступним чином. Поділимо відрізок [0,
1] на три рівні частини і покладемо, що
у всіх точках середньої частини наша
функція дорівнює
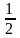 .
Потім ліву і праву третини знову розділимо
на три рівні частини і покладемо, що від
.
Потім ліву і праву третини знову розділимо
на три рівні частини і покладемо, що від
 до
до
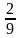 функція рівна
функція рівна
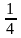 ,
а від
,
а від
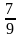 до
до
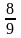 вона рівна
вона рівна
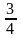 .
Тепер залишилося чотири відрізки, на
яких функція ще не визначена:
.
Тепер залишилося чотири відрізки, на
яких функція ще не визначена:
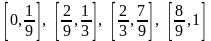 .
.
Розділимо
кожен з них на три рівні частини і на
кожній з середніх частин покладемо
функцію, рівну відповідно
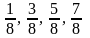 .
.
Продовжуючи цей процес, ми отримаємо функцію, яка визначена у всіх точках, які не належать канторовій множині. Її легко визначити і в точках цієї множини так, щоб вона стала після цього неперервною і неспадною. Графік отриманої функції наближено зображено на рис. 1.4. Він має вигляд драбини з нескінченним числом сходинок і саме тому отримав назву “чортова драбина” [11:134].
Отже,
після того, як ми познайомились з лініями,
які мають нескінченно багато максимумів
і мінімумів, драбиною з нескінченним
числом сходинок навряд чи когось здивуєш.
Але дивно інше. Підрахуємо загальну
довжину всіх сходинок нашої драбини.
Перша сходинка має довжину
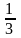 ,
дві другі – по
,
наступні чотири сходинки мали довжину
по
,
дві другі – по
,
наступні чотири сходинки мали довжину
по
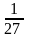 і так далі. Таким чином, сума довжин всіх
сходинок виражається нескінченною
спадною геометричною прогресією
і так далі. Таким чином, сума довжин всіх
сходинок виражається нескінченною
спадною геометричною прогресією
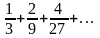
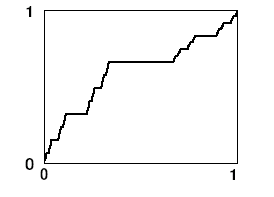
Рис. 1.4.
Сума цієї прогресії рівна
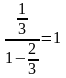 .
.
Таким чином, загальна довжина всіх сходинок рівна 1. Але на цих сходинках функція зовсім не піднімається вгору, весь її підйом зосереджений в точках канторової множини. А на долю цієї множини залишилось дуже «мало» точок – хоча її потужність і рівна континууму, але довжина рівна нулю! (Довжина всього відрізка [0, 1] рівна 1, загальна довжина сходинок рівна 1). Таким чином, наша функція піднімається вгору на 1, хоча росте лише на множині нульової довжини і не робить ніде стрибків! Дивно, чи не так?
1.1.3
К а н т о р і в с ь к і
ч и с л а. Ті
числа відрізка [0, 1], які в трійковій
системі числення зображаються за
допомогою цифр 0 та 2 називають
канторівськими
числами.
Введемо в множині операцію * за
правилом: 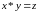 ,
де
,
де 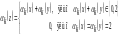 якщо:
якщо: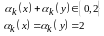
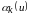 -
-
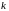 -тий
трійковий знак числа
-тий
трійковий знак числа
 .
.
Лема 1. Множина канторівських чисел разом з введеною операцією множення утворює комутативну групу.
Доведення.
Очевидно, що
 є канторівським числом, тобто
є канторівським числом, тобто
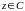 і операція * є замкненою. Більше того,
для довільної трійки канторівських
чисел
і операція * є замкненою. Більше того,
для довільної трійки канторівських
чисел
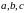 має місце рівність
має місце рівність
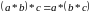 .
.
Очевидно
також, що справедливі рівності
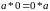 і
і
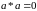 для кожного канторівського числа
для кожного канторівського числа
 .
Таким чином введена операція для
канторівських чисел є замкнена і для
неї виконуються всі групові аксіоми,
тобто
.
Таким чином введена операція для
канторівських чисел є замкнена і для
неї виконуються всі групові аксіоми,
тобто
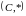 є групою. Оскільки
є групою. Оскільки
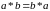 ,
то ця група є комутативною. Доведено.
,
то ця група є комутативною. Доведено.
