3.2. Двовимірне узагальнення килима Серпінського

Що вийде, якщо поділити квадрат на дев’ять рівних квадратів і вилучати не середній квадрат, а будь-який інший квадрат або квадрати?

В результаті можна отримати, очевидно, 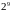самоподібних об’єктів включаючи килим Серпінського, цвинтар Серпінського і множину Кантора. Їх площа буде такою ж як і у килима Серпінського. Спосіб підрахунку площ аналогічний до підрахунку площі килима Серпінського. Будемо вважати однаковими ті з них, які отримуються один з одного шляхом симетрії відносно всіх ліній симетрії початкового квадрата або (та) поворотом на кут кратний 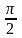відносно центру квадрата.

Підрахуємо скільки таких різних об’єктів існує. Для цього скористаємося теоремою Пойа [15]. Отже, утворимо твірну функцію запасу для самосуміщень квадрату. Маємо:

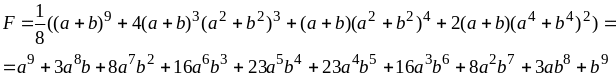
Дана функція дозволяє визначити скільки існує об’єктів даної розмірності. Наприклад, треба визначити скільки існує об’єктів розмірності 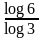. Для цього треба знайти коефіцієнт біля 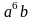. Отже, об’єктів розмірності існує рівно 16.

Тому, знайшовши суму всіх коефіцієнтів визначимо, що всього таких об’єктів 102, але серед них є квадрат і порожня множина, тобто залишається рівно 100 об’єктів [5].

Варіанти перших етапів побудови різних об’єктів зображено на рис. 3.3.

Рис. 3.3.

Отримані об’єкти можна погрупувати за розмірностями. На рис 3.3. об’єкти з однаковою розмірністю розташовані в одному рядку.

В додатку А наведені деякі фрактальні множини, які отримуються шляхом вилучення з квадрата менших квадратів.

3.3. Аналоги килима Серпінського в тривимірному просторі

3.3.1. Ф р а к т а л ь н а п і н а а б о ”Я б л у к о”.

Буквальне узагальнення килима Серпінського на простір починається з видалення з куба середнього підкуба (27-ї частини об’єму вихідного куба), після чого залишається „оболонка” із 26 підкубів. Продовжуючи видаляти з кожного підкуба центральний куб отримаємо фрактал, який називається фрактальною піною [13:194]. ЇЇ розмірність .

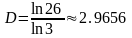Кожен центральний кубик, точки якого видаляли, з усіх сторін оточений неперервною границею, розділеною на нескінченну множину нескінченно тонких шарів нескінченної щільності. Для того, щоб потрапити з точки, що знаходиться в одному з центральних кубів, до точки, що розміщена в іншому центральному кубі, необхідно пройти через нескінченну кількість шарів.

Для того щоб аналітично задати „яблуко” будемо й надалі використовувати точки в трійковій системі числення виду (для 3-х вимірного простору):

,

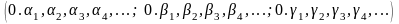де .

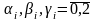Якщ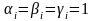о , , то ми отримаємо „яблуко”.

По-іншому, аналітичне задання цієї множини виглядає наступним чином:

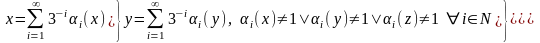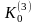, де - множина точок фрактальної піни.

3.3.2. Г у б к а М е н г е р а. Ще одним просторовим аналогом квадратного килима Серпінського (а отже і множини Кантора) є так звана губка Менгера (Menger sponge). Процес її утворення полягає в тому, що кожна грань куба з ребром, що має одиничну довжину, ділиться на 9 рівних квадратиків. так само, як і при побудові квадратного килима Серпінського. В результаті вихідний куб розбивається на 27 однакових кубиків з довжиною ребра, що дорівнює . Потім, видаляючи 7 кубиків (один центральний та 6 із центру кожної грані), протилежні грані вихідного куба з’єднуються наскрізним центральним отвором квадратної форми. В результаті з 27 залишається 20 маленьких кубиків (рис. 3.4).

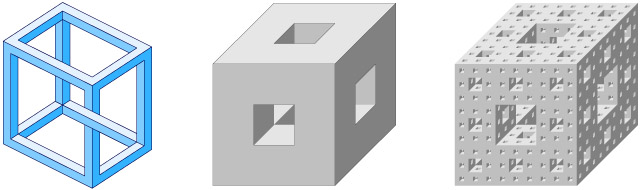
Рис. 3.4.

На наступному кроці це саме проробляємо з кожним кубиком, що залишився, і т. д. В результаті ми отримаємо деяку фігуру – губку Менгера (див. рис. 3.4).

Рис. 3.4. Губка Менгера

Така ітераційна процедура з вирізанням наскрізних отворів і подальшого перетворення кожного кубика, що залишився, у 20 ще менших кубиків з розміром втричі меншим вихідного продовжується до нескінченності.

Фрактальна розмірність губки Менгера дорівнює 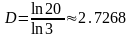. Оскільки 2<D<3, то це говорить про те, що губка має нульовий об’єм, але площа поверхні її пор – нескінченна. В цьому фракталі і та множина, що залишилася, і та, яку видалили, є зв’язними множинами [4:24].

Для того щоб аналітично задати губку Менгера будемо й надалі використовувати точки в трійковій системі числення виду (для 3-х вимірного простору):

,

де .

Якщ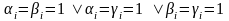о , , то ми отримаємо губку Серпінського.

По-іншому, аналітичне задання цієї множини виглядає наступним чином:

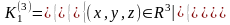
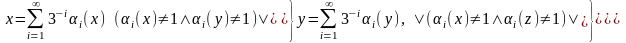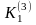, де - множина точок губки Менгера.

3.3.3. О б’є м н и й п и л К а н т о р а. Звичайно, як і в просторі R², узагальненням множини Кантора на тривимірний простір буде і декартів добуток трьох множин Кантора (рис. 3.5). Отримуємо цю множину, коли з вихідного одиничного куба, поділеного, як описано вище, на 27 кубиків, видаляємо 19 кубиків, залишаючи їх лише в кутах вихідного куба. Зрозуміло, що фрактальна розмірність цієї множини .

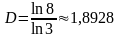Рис. 3.5. Об’ємний пил Кантора.

Для того щоб аналітично задати обємний пил Кантора будемо й надалі використовувати точки в трійковій системі числення виду (для 3-х вимірного простору):

,

де .

Якщо 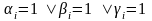, , то ми отримаємо пил Кантора.

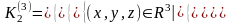
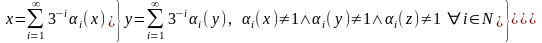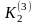По-іншому, аналітичне задання цієї множини виглядає наступним чином: , де - множина точок пилу Кантора.