
- •I. Практическое занятие 1
- •1.1. Статические моменты.
- •I.I.I. Центр тяжести сложного сечения
- •1.1.2. Задачи для самостоятельного решения
- •I.2.I. Главные оси и главные моменты инерции
- •1.2.2. Вычисление моментов инерции сложных сечений
- •1.2.3. Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •2. Практическое занятие 2
- •2.1. Продольные силы
- •2.2. Напряжения, перемещения и деформации
- •2.3. Потенциальная энергия деформации
- •2.4. Пластичность материала
- •2.5. Расчет на прочность
- •2.5. Задачи для самостоятельного решения
- •2.7. Вопросы для самоконтроля
- •3. Практическое занятие 3
- •3.1. Основные понятия и определения
- •3.2. Внутренние силовые факторы
- •3.2.1. Правило знаков для изгибающих моментов и поперечных сил
- •3.2.2. Построение эпюр изгибающих моментов и поперечных сил
- •3.3. Задачи для самостоятельного решения
- •3.4. Вопросы для самопроверки
- •4. Практическое занятие 4
- •4.1. Чистый изгиб. Нормальные напряжения при изгибе
- •4.2. Поперечный изгиб. Касательные напряжения при изгибе
- •4.3. Расчеты на прочность
- •4.4. Задачи для самостоятельного решения
- •4.5. Вопросы для самопроверки
- •5. Практическое занятие 5
- •5.1. Сдвиг
- •5.2. Кручение
- •5.2.1. Крутящий момент
- •5.2.2. Расчеты на прочность и жесткость
- •5.3. Задачи дли самостоятельного решения
- •5.4. Вопросы для самопроверки
- •6. Практическое занятие 6
- •6.1. Совместное действие кручения и изгиба
- •6.2. Совместное действие кручения, изгиба и растяжения (сжатия)
- •6.3. Задачи для самостоятельного решения
- •6.4. Вопроса для самопроверки
- •644099, Омск, ул. Красногвардейская, 9
3.2.2. Построение эпюр изгибающих моментов и поперечных сил
Рекомендуется следующий порядок построения эпюр М и Q:
1. Составляется расчетная схема балки (в виде оси) с изображением действующих на неё нагрузок.
Отбрасываются опоры, а их действие на балку заменяется соответствующими реакциями; указываются обозначения реакций и принятие их направления.
Составляются уравнения равновесия бачки, решением которых определяются значения опорных реакций.
Балка разбивается на участки, границами которых являются точки приложения внешних сосредоточенных сия (включая реакции) и моментов, а также точки начала и окончания действия или изменения характера распределенных нагрузок.
5. Составляются выражения изгибающих моментов М (Мх, My), поперечных сил (Qх, Qy) для каждого участка балки. В сечениях балки рекомендуется указывать направление изгибающего момента и поперечной силы положительными с учетом правил знаков. В этом случае полученные в результате расчетов знаки М и Q будут определять знак изгибающего момента и поперечной силы.
Н а расчетной схеме указываются начало и направление отсчета расстояний Z для каждого участка.
6. По полученным выражениям исчисляются ординаты эпюр для сечений балки в количестве, достаточном для изображения этих эпюр.
7. Определяются сечения в которых поперечные силы равны и в которых, следовательно, действуют экстремальные изгибающие моменты; вычисляются значения этих моментов.
8. По полученным значениям ординат строятся эпюры.
9. Производится проверка построении эпюр путем сопоставления их друг с другом: если на участке нет внешних нагрузок, то эпюры М и Q линейные (причем прямая эпюры Q - параллельна нулевой линии этой эпюры); если на участке действует равномерно распределенная нагрузке, то эпюра М - нелинейная - квадратная парабола; в точке приложения сосредоточенной силы (в том числе реакции) на эпюре поперечных сил соответствует "скачок" на величину этой силы, а на эпюре изгибающих моментов - перелом линии; в точках приложения сосредоточенных моментов эпюра поперечных сил не меняется, а на эпюре изгибающих (их моментов наблюдается "сжатие" на величину этого моментa.
В ряде случаев отдельные этапы построения эпюр из приведениях выше можно не выполнять. Например, можно не изображать балку без эпюр, а обозначение и направление опорных реакций можно указывать на расчетной схеме балки; при расчете балок, заделанных одним концом, нет необходимости определять опорные реакции.
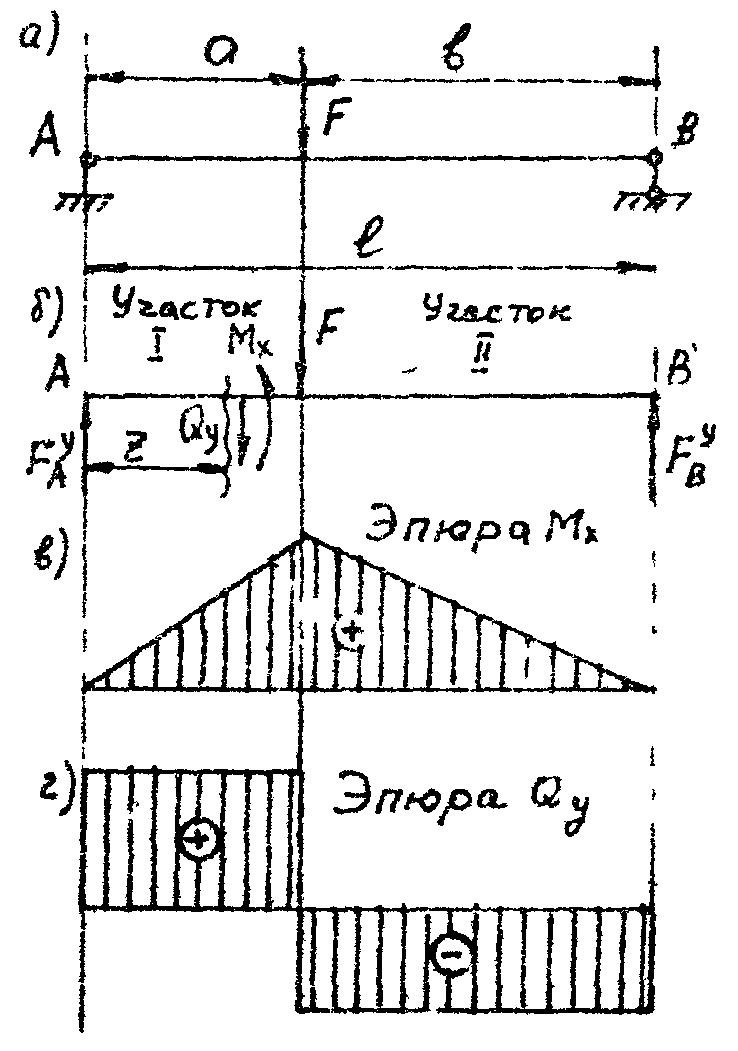
Пример 3.1. Построить эпюры Мх и Qy для балки, показанной на рис. 3.4,а.
Решение. Из условия равновесия определяем опорные реакции (рис. 3.4,б):
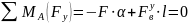 ;
;
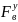 = F
= F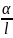
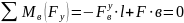
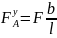
Проверяем:
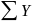 =
=
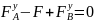
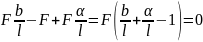 ,
0=0.
,
0=0.
Следовательно, опорные реакции определены правильно.
Paccматривая балка имеет два участка (рис. 3.4,б).
Пользуясь методом сечений, вычисляем изгибающие моменты и поперечные силы на этих участках.
У часток I (0 ≤ Z ≤ α)
Согласно (3.1.)
М
х
=
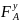 ∙ Z
=
∙ Z
=
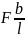 ∙
Z,
Qy
=
=
∙
Z,
Qy
=
=
или, используя (3.3),
Qy
=
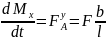
П ри Z = 0
Мх = 0,
Qy =
П
ри
Z
= α, Мх
=
∙α=
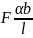 ,
Qy
=
,
Qy
=
У часток II (0 ≤ Z ≤ ℓ)
М
х
=
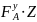 – F
(
– F
(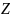 - α),
Qy
=
- α),
Qy
=
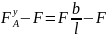 = -
= -
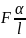
или
Qy
=
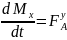 -
= -
-
= -
П ри Z = α, Мх =
П
ри
Z
= ℓ, Мх
=
∙ ℓ - F
(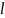 - α)
=
∙
ℓ -
∙
b = 0
- α)
=
∙
ℓ -
∙
b = 0
По полученным значениям Мх строим эпюру изгибающих моментов (рис. 3.4,в), а по значениям Qy - эпюру поперечных сил (рис. 3.4,г).
Проводя проверку эпюр в соответствии с п.9 рекомендаций их построений, убеждаемся в их правильности.
Пример 3.2. Построить эпюры Мх и Qy для балки, показанной на рис. 3.5,е.
Решение.
Благодаря симметрии системы опорные
реакции FA
= FB
=
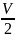
Балка содержит лишь один участок АВ.
И згибающий момент в сечении Z (рис. 3.5, б)
М
х
=
FA
∙ Z
– q
∙ Z
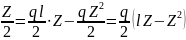
Поперечная
сила
Qy
=
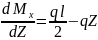
При Z = 0, Мх = 0
Qy
= q
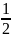
П
ри
Z
=
;
Мх
=
q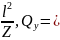 0
0
Эпюра изгибающих моментов (парабола) показана на рис. 3.5,в, а эпюра поперечных сил – на рис. 3.5,г.
Анализ эпюр подтверждает их правильность.
Пример 3.3. Построить эпюры Мх и Qy для балки, показанной на рис. 3.6, а
Решение. Проводим сечение на расстоянии Z от точки В.
Условие равновесия сил, действующих на отсеченную правую часть (рис. 3.6,б) имеет вид
М
х
=-
FZ, Qy
= F или Qy
= -
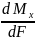 = F
= F
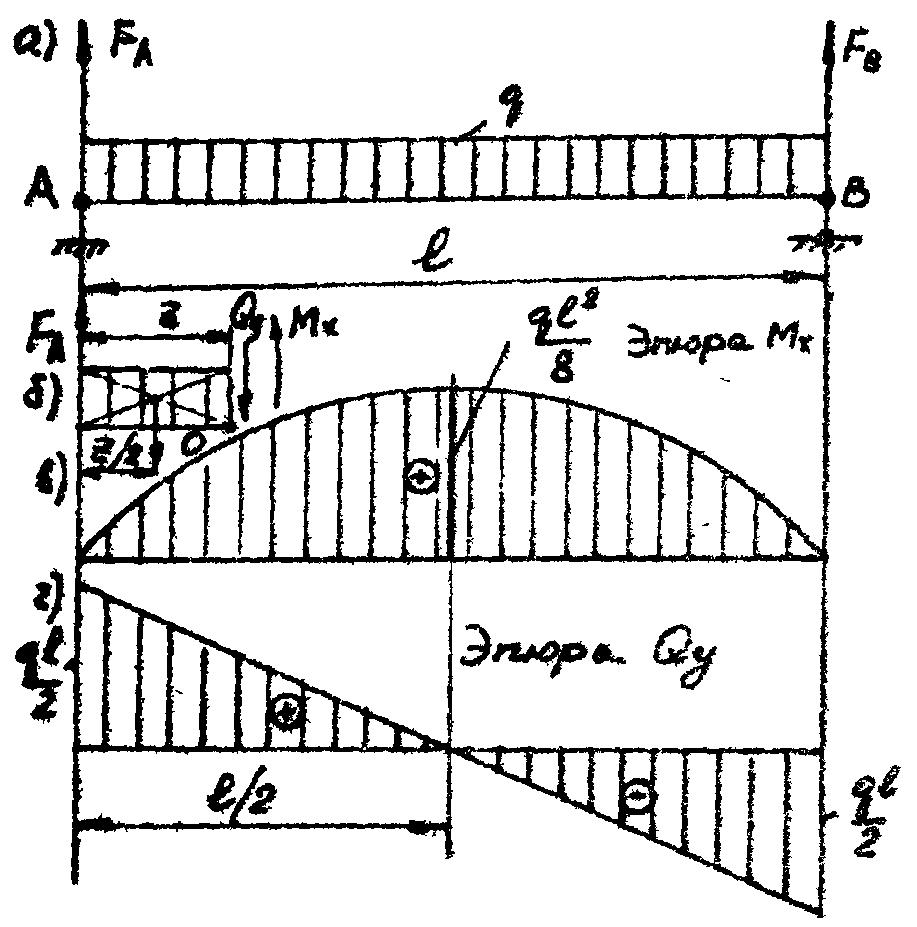
Рис. 3.5
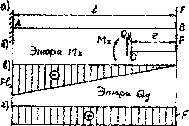
Рис. 3.6
П ри Z = 0, Мх = 0, Qy = F
При Z = ℓ, Мх =- Fℓ, = F
По полученным значениям Мх и Qy строим эпюру изгибающих моментов (рис. 3.6,в) и эпюру поперечных сил (рис. 3.6,г). Делаем анализ построенных эпюр, убеждаемся в их правильности.
Пример 3.4. Построить эпюры Мх и Qy для балки, показанной на рис. 3.7,б.
Р ешение. Проводим сечение на расстоянии Z от точки В.
Из определения изгибающего момента поперечной силы (3.2) находим
Мх
=-
q ∙Z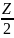 ,
Qy
= qZ или используя зависимость (3.3),
,
Qy
= qZ или используя зависимость (3.3),
Q
y
= - (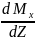 )
= qZ
)
= qZ
П ри Z = 0, Мх = 0, Qy = 0
П
ри
Z
= ℓ, Мх
=-
q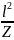 ,
Qy
= qℓ
,
Qy
= qℓ
П
ри
Z
=
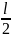 ,
Мх
=-
q
,
Qy
= q
,
Мх
=-
q
,
Qy
= q
По полученным значениям Мх и Qy строим эпюру изгибающих моментов (рис. 3.7,в) и эпюру поперечных сил (рис. 3.7,г).
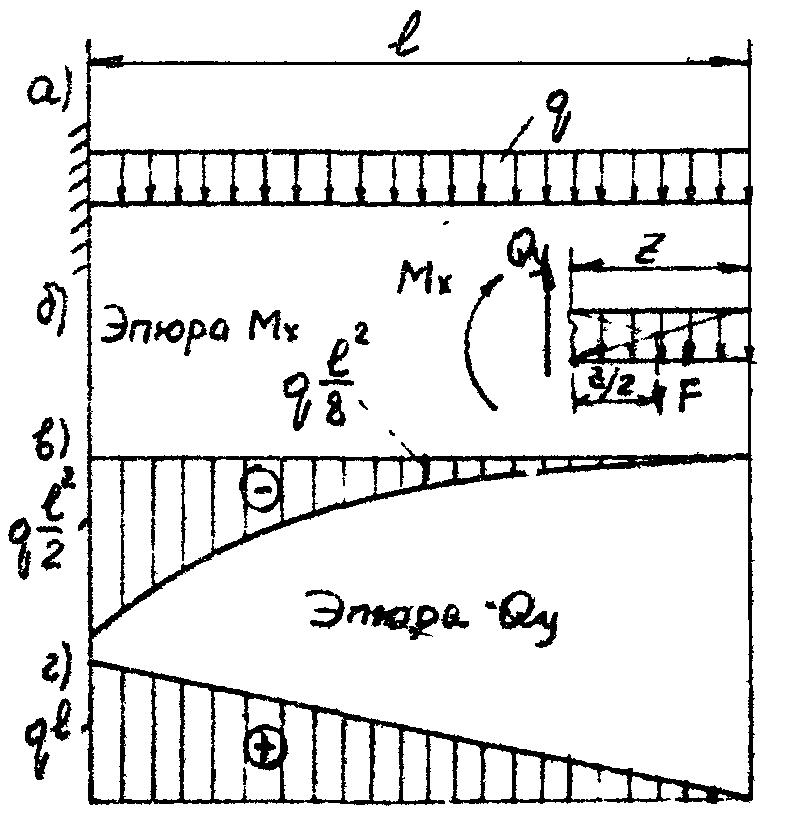
Рис. 3.7
Пример
3.5. Построить эпюры Мх
и Qy
для
балки, показанной на рис. 3.8,а, если
F = 100 кН, М =100 кН ∙ м, q
= 200
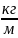 ,
α = 2 м, b = c = 1 м.
,
α = 2 м, b = c = 1 м.
Решение. Заменяя действие эпюр их реакциями, используем расчетную схему, представленную на рис. 3.8,б. Из условий равновесия определяем опорные реакции:
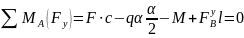 ;
;
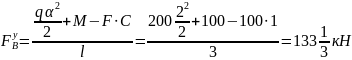
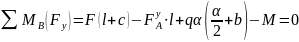
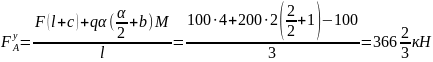
Проверяем
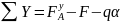 +
+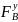 = 0
= 0
366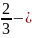 100
- 200∙2 +133
100
- 200∙2 +133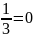 ,
0 = 0
,
0 = 0
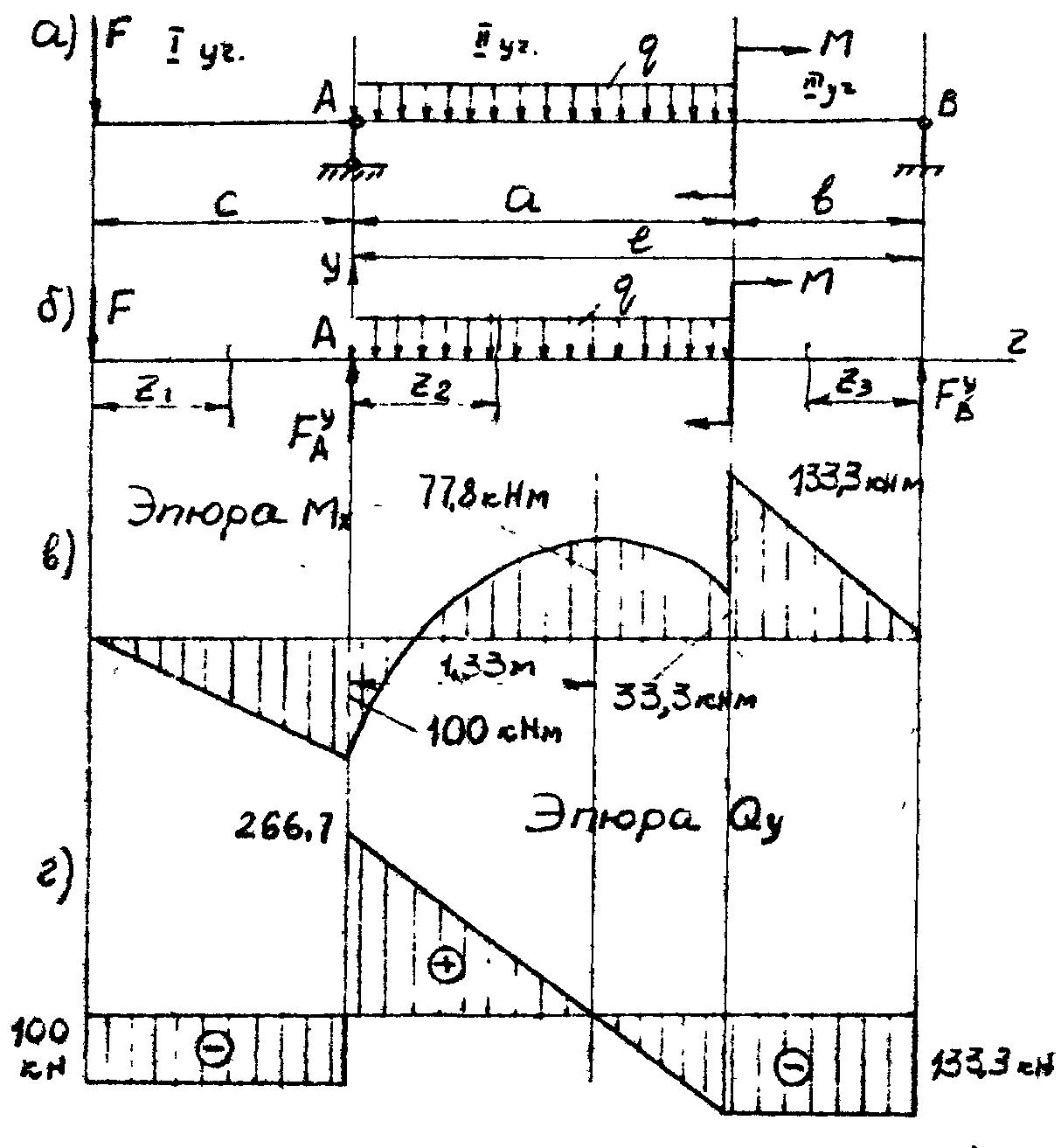
Рис. 3.8
Для построения эпюр Мх и Qy пользуемся приведенными правилами.
У часток I (0 ≤ Z1 ≤ С = 1 м).
И згибающий момент в сечении с абсциссой Z1 Мх = - FZ1
П
оперечная
сила в этом сечении Qy
=
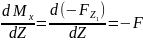
П ри Z1 = 0, Мх = 0, Qy = - 100 кН
П ри Z1 = 1 м, Мх = - 100 кН∙м, Qy = - 100 кН
У часток II(0 ≤ Z2 ≤ α = 2 м).
И
згибающий
момент Мх
=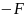 (С
+ Z2)
+
∙
Z2-q
(С
+ Z2)
+
∙
Z2-q
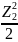 .
.
П
оперечная
сила
Qy
=
= - F +
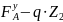
П ри Z2 = 0 Мх =- F∙ C = - 100∙1 = - 100 кН∙м
Qy = - F + = - 100 + 366,7 = 266,7 кН
П
ри
Z2
= 2 Мх
=-100(1+2)+
366,7∙2 - 200∙2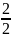 = 33,4 кН∙м
= 33,4 кН∙м
Qy = - 100 + 366,7 - 200∙2= - 133,3кН
Д ля построения эпюры Мх на участке необходимо определить ординату эпюры хотя бы в одной промежуточной точке. Определим абсциссу Z2, соответствующую экстремальному значению изгибающего момента (поперечная сила в этом сечении равна нулю):
Q
y
=
= 0, - F +
- q
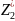 = 0
= 0
Откуда
находим
=
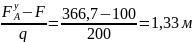
П
ри
Z2
=
= 1,33 м Мх
=-
100(1+1,33) +366,7∙1,33 – 200
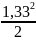 = 77,8 кН∙м
= 77,8 кН∙м
Участок III (0 ≤ Z3 ≤ b = 1 м).
И згибающий момент и поперечная сила в сечении с абсциссой Z3 соответственно равны Мх = ∙Z; Qy = -
При
Z3
= 0, Мх
=
0, Qy
= 133
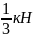
Z3
= 1 м, Мх
=133
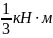 ,
Qy
= 133
,
Qy
= 133
По полученным значениям Мх и Qy строим эпюру изгибающих моментов (рис. 3.8,в) и эпюру поперечных сил (рис. 3.8,г). Анализ эпюр Мх и Qy подтверждает их правильность.
