1.1.2. Задачи для самостоятельного решения

Задача 1.1. Для одного из сечений, показанных на рмс.1.7, 1.8, 1.9 определить положение его центра тяжести, учитывая симметрию сечения.

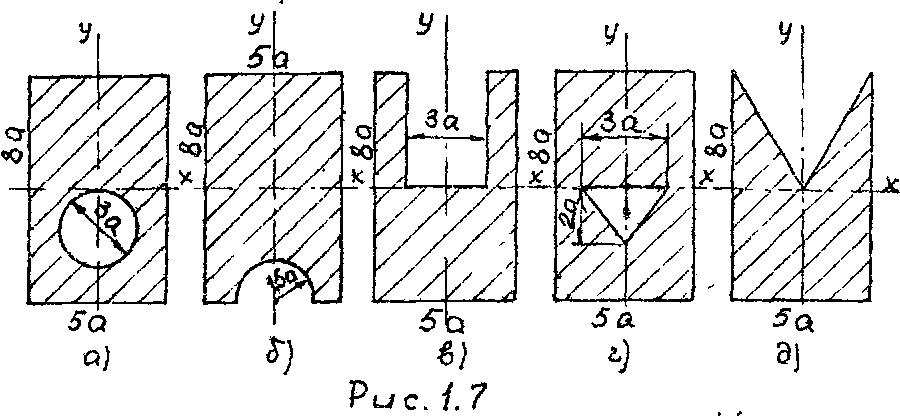
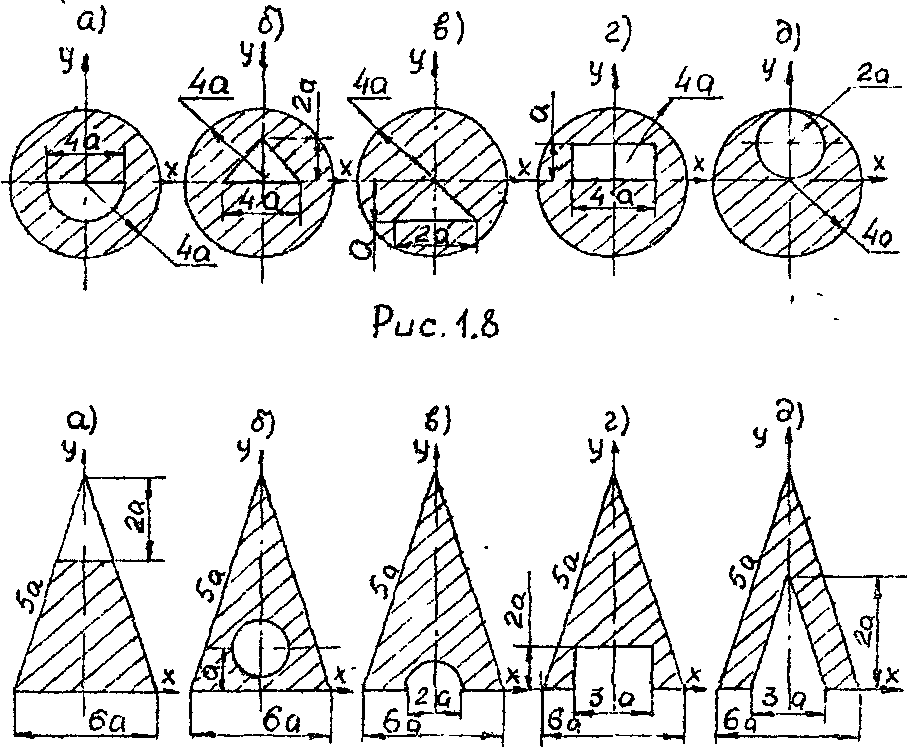
Рис. 1.9

Задача 1.2. Для одного из сечений, показанных на рис.1.10, определить положение его центра тяжести.

1 .2. Моменты инерции

Рис. 1.11

Осевыми моментами площади сече­ния называются выражения сле­дующего вида

(1.8)

Интеграл вида

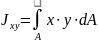(1.9)

называется центробежным момен­том инерции площади сечения от­носительно осей X и У.

Интеграл вида

J_p = (1.10)

называется полярным моментом инерции площади сечения.

Осевые и полярный моменты инерции связаны зависимостью

J_p = J_x+J_y (1.11)

Осевые и полярные моменты инерции всегда положительные. Центробежный момент инерции может быть больше, меньше или равен нулю. Моменты инерции измеряются в см⁴,м⁴.

При параллельном переносе осей координат (рис. 1.11).

J_y = 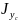+ A∙a²

J_x = + A∙b²

J_xy = 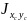+ A∙a∙b

J_p =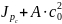 (1.12)

где ,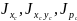 - соответствующие моменты инерции относительно центральных осей (начало координат в центре тяжести площади сечения), параллельных осям X и У ; а и b - расстояние между осями у и у_с, х и х_с; с₀ - расстояние между началом координат системы Х_с О У_с .

I.2.I. Главные оси и главные моменты инерции

Две взаимно перпендикулярные оси, относительно которых центро­бежный момент площади сечения равен нулю, называются главными осями инерции, а моменты инерции относительно этих осей называются глав­ными моментами инерции.

Если же эти оси к тому же является центральными, то моменты инерции относительно них называются главными центральными.

Главные моменты инерции имеют экстремальные значения: один из них - максимальный J_max, другой - минимальный J_min и определя­ются по формуле

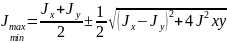(1.13)

где J_х , J_у и J_ху - осевые и центробежный моменты инерции относительно произвольно взятых осей х и у .

Знак «плюс» принимается при вычислении J_max , "минус" - при вычислении J_min.

При повороте осей на угол

J_y1 = J_ycos² + J_xsin² -

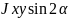
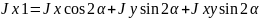(1.14)

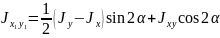
Существует зависимость

J_max+ J_min = J_x + J_y = const (1.15)

Положение главных осей относительно произвольно взятых, опре­деляется углом :

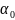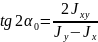(1.16)

Пример 1.6. Определить осевые моменты сечения прямоугольной формы

(рис.1.12) относительно осей, проходящих через центр тяжести сечения С.

Рис. 1.12

Решение. Выделим элемент площа­ди dA = b∙dy на расстоянии у от оси X .

Тогда

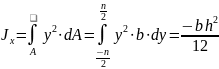
Аналогично находим

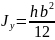
Таким образом

(1.17)

Пример 1.7. Определить полярный и осевые моменты инерции кру­га радиуса R относительно его центра и центральных осей (рис. 1.13).

Решение. Выделим из круга элементарное кольцо толщиной dp, радиусом ρ и площадью dA = 2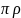 ∙ dp

П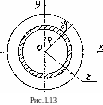 олярный момент инерции элемен­тарного кольца относительно центра круга О dJ_p = ρ²dAd

Подставляя значение dA интег­рируя, получим

(1.18)

Так как для круга J_х = J_у и J_x + J_y = J_p, то

J_х = J_у = 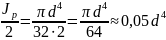(1.19)

Пример 1.8. Определить осевые моменты инерции J_х и 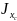сечения треугольной формы (рис. 1.14).

Рис. 1.14

Решение. Выделим элементарную площадку с ординатой у и пло­щадью dA = by∙dy. Из рис 1.14 видно, что

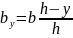(1.20)

Используя выражение (1.20), на­ходим

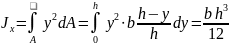
Из (1.21) находим

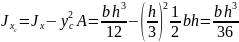(1.21)