
- •I. Практическое занятие 1
- •1.1. Статические моменты.
- •I.I.I. Центр тяжести сложного сечения
- •1.1.2. Задачи для самостоятельного решения
- •I.2.I. Главные оси и главные моменты инерции
- •1.2.2. Вычисление моментов инерции сложных сечений
- •1.2.3. Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •2. Практическое занятие 2
- •2.1. Продольные силы
- •2.2. Напряжения, перемещения и деформации
- •2.3. Потенциальная энергия деформации
- •2.4. Пластичность материала
- •2.5. Расчет на прочность
- •2.5. Задачи для самостоятельного решения
- •2.7. Вопросы для самоконтроля
- •3. Практическое занятие 3
- •3.1. Основные понятия и определения
- •3.2. Внутренние силовые факторы
- •3.2.1. Правило знаков для изгибающих моментов и поперечных сил
- •3.2.2. Построение эпюр изгибающих моментов и поперечных сил
- •3.3. Задачи для самостоятельного решения
- •3.4. Вопросы для самопроверки
- •4. Практическое занятие 4
- •4.1. Чистый изгиб. Нормальные напряжения при изгибе
- •4.2. Поперечный изгиб. Касательные напряжения при изгибе
- •4.3. Расчеты на прочность
- •4.4. Задачи для самостоятельного решения
- •4.5. Вопросы для самопроверки
- •5. Практическое занятие 5
- •5.1. Сдвиг
- •5.2. Кручение
- •5.2.1. Крутящий момент
- •5.2.2. Расчеты на прочность и жесткость
- •5.3. Задачи дли самостоятельного решения
- •5.4. Вопросы для самопроверки
- •6. Практическое занятие 6
- •6.1. Совместное действие кручения и изгиба
- •6.2. Совместное действие кручения, изгиба и растяжения (сжатия)
- •6.3. Задачи для самостоятельного решения
- •6.4. Вопроса для самопроверки
- •644099, Омск, ул. Красногвардейская, 9
2.3. Потенциальная энергия деформации
При статическом нагружении стержня постоянного сечения А, длиной ℓ, силой F с модулем линейной упругости E потенциальная энергия деформации
U
=
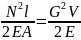 (2.7)
(2.7)
где N - продольная сила, Н;
V= A ∙ ℓ - объем стержня.
При одновременном действии нескольких сил на стержень со ступенчатым изменением поперечных размеров при напряжениях, не превышающих предела пропорциональности, потенциальная энергия деформации
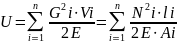 (2.8)
(2.8)
где n - число участков, отличающихся значением напряжений G;
Gi - нормальное напряжение в поперечных сечениях i-го участка;
Ni - продольная сила в поперечных сечениях на i-том участке;
Vi , Ai , ℓi - соответственно объем, площадь сечения и длина i-го участка.
Пример 2.5. Определить потенциальную энергию деформации стержня по данным и полученным результатам примера 2.2.
Решение. Для вычисления потенциальной энергии деформации стержня воспользуемся формулой (2.8)
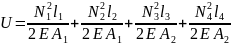
Так как в нашем случае l1 = l2 и l3 = l4, то
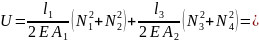
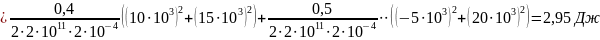
2.4. Пластичность материала
Пластичность материала характеризуется остаточным относительным удлинением
δ
=
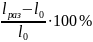 (2.9)
(2.9)
где ℓраз - длина образца после paзрыва, измеренная после соединения частей разорванного образца;
и остаточным относительным сужением
Ψ
=
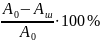 (2.10)
(2.10)
где Aш - площадь поперечного сечения разорванного образца в наиболее тонком месте шейки.
Пример 2.5. Круглый стальной стержень длиной 200 мм и диаметром 20 мм разорван на испытательной машине. После разрыва общая длина частей стержня составляет 252 мм, а наименьший диаметр шейки равен 14,5 мм. Определить остаточное относительное удлинение образца δ и остаточное относительное сужение шейки Ψ.
Решение. Остаточное относительное удлинение образца определяем по формуле (2.9):
δ
=
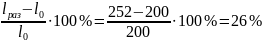
Остаточное относительное сужение находим по формуле (2.10):
Ψ
=

 47,4 %
47,4 %
2.5. Расчет на прочность
Условие прочности при растяжении (сжатии)
G
=
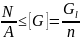 (2.11)
(2.11)
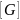 – допускаемое
нормальное напряжение;
– допускаемое
нормальное напряжение;
Gl – предельное нормальное напряжение (для пластичных материалов Gl = GТ, для хрупких - Gl = Gв)
n - коэффициент запаса прочности.
При проверочном расчете определяют фактическое напряжение и сравнивают его с допускаемым
При проектном расчете определяют размер поперечного сечения стержня
А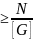 (2.12)
(2.12)
Для
определения допускаемой нагрузки
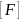 находят
допускаемую
находят
допускаемую
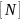 продольную
силу, а затем по ней находят
продольную
силу, а затем по ней находят
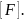
Например 2.6. На рис.2.3,а показан металлический стержень, а на рис.2.3,б - эпюра N продольных сил, возникающих а его поперечных сечениях. Произвести расчет стержня на прочность в указанных ниже случаях.
I. Стержень изготовлен из пластичной стали:
=
160 МПа,
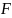 = 30 кН, А1
=
10 см2,
А2
= 4 см2
= 30 кН, А1
=
10 см2,
А2
= 4 см2
Проверить прочность стержня.

Рис. 2.3
Решение. Поперечные сечения участка III стержня не могут быть опасными, так как в них предельная сила меньше (по абсолютной величине), чем в сечениях участка II, а площади поперечных сечений участков II и III одинаковы. Опасными могут быть сечения участка I или II. Определим нормальные напряжения в них:
G1
=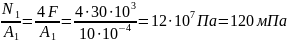
GII
=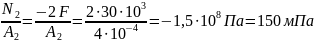
Стержень является прочным, так как угловые прочности (2.16) выполняются
G1 = 120 мПа < = 160 мПа
GII
=
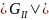 = 150 мПа <
= 150 мПа <
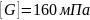
2. Стержень изготовлен из чугуна:
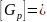 80
мПа,
80
мПа,
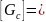 150 мПа, F =30 кН, А1
= 10
см2,
А2
= 4 см2
150 мПа, F =30 кН, А1
= 10
см2,
А2
= 4 см2
Проверить прочность стержня.
Решение. Определим нормальные ускорения в поперечных сечениях участков I, II и III стержня:
G1 =
GII =
GIII
=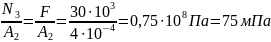
Снижающие
напряжения GII
=
-
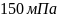 удовлетворяют условию прочности
удовлетворяют условию прочности
Gс
=
= 150 мПа ≤
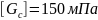
Наибольшие растягивающие напряжения G1 =120 мПа не удовлетворяют условию прочности (2.11):
Gр
= G1∙
120 мПа >
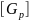 = 80 мПа
= 80 мПа
Следовательно, прочность стержня недостаточна.
3. Стержень изготовлен из пластичной стали:
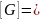 160
мПа, F
= 30 кН. Подобрать площадь А1
поперечных сечений для участка 1 и А2
для участков II
и III.
160
мПа, F
= 30 кН. Подобрать площадь А1
поперечных сечений для участка 1 и А2
для участков II
и III.
Решение. По формуле (2.11)
А1
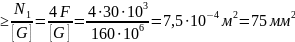
А2
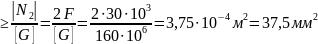
Принимаем
А1
=
75
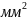 ,
А2
= 38
,
А2
= 38
4. Стержень изготовлен из пластичной стали:
160 мПа, А1 = 10 см2, А2 = 4 см2
Определить допускаемое значение нагрузки .
Решение. Определяем допускаемые (по условию прочности) значения продольных сил:
 =
=
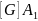 =
160 ∙106∙10∙10-4=16∙104
Н = 160 кН
=
160 ∙106∙10∙10-4=16∙104
Н = 160 кН
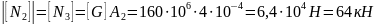
Из эпюры N (рис. 2.3, б) следует, что
N1
=
4F,
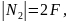 N3
= F
N3
= F
Тогда из условия прочности для участка I стержень
N1 = 4F ≤ = 160 кН,
откуда F ≤ 40 кН;
Для
участка II:
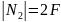 ≤
≤
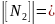 64 кН,
64 кН,
откуда F ≤ 32 кН;
Для
участка III: N3
= F
≤
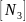 =
64 кН,
=
64 кН,
откуда F ≤ 64 кН.
Допускаемое значение нагрузки , при котором условие прочности (2.11) выполняется для всех участков стержня, равно меньшему из найденных значений, т.е. = 32 кН.
Пример 2.7. В швейном производстве применяется пресс ПЛИм с пневматическим приводом. Поршень силового цилиндра (рис. 2.4) прессе имеет диаметр D = 12 см, в шток поршня - диамотр d = 1,6 см.
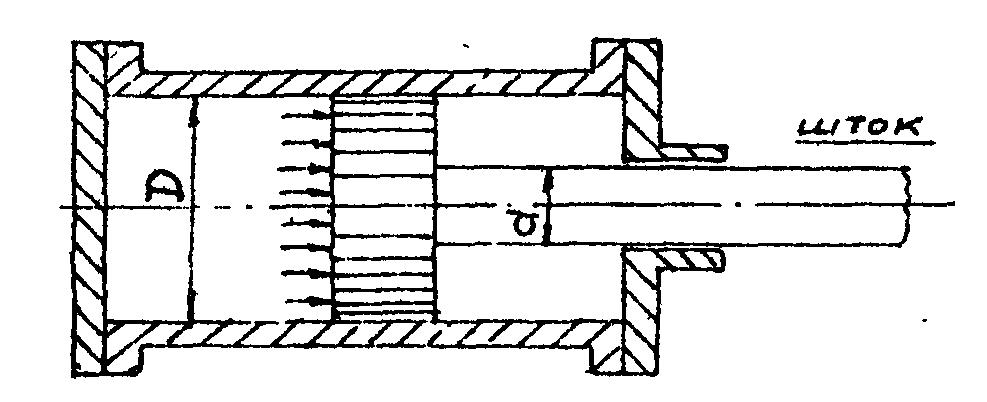
Рис. 2.4.
Давление сжатого воздуха q = 6 ∙ 105 Па. Найти наибольшее напряжение в штоке. Решение. Напряжение в штоке
G
=
где Аш - площадь поперечного сечения штока,
Аш
=
 2,01
см2
2,01
см2
/\/ - продольная сипя в сечении штока, равная силе давления на поршень.
N
= Fn
= q∙An
= q∙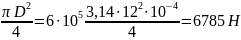
Напряжение в штоке
G
=
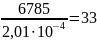 ,76
,76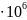 Па
= 33,76 мПа
Па
= 33,76 мПа
