3. Механічні коливання

Багатьом процесам, що відбуваються в біологічних системах, властива періодичність. Вона спостерігається у функціональній діяльності серця, легенів, шлунка. Деякі процеси у живих організ­мах можна вважати коливальними: коливання стінок судин при поширення пульсових хвиль, коливання тиску крові у судинах, об’єму повітря у легенях, коливання барабанних перетинок, голосових зв’я­зок, значень біопотенціалів у різних точках тіла людини. Для визначення норми або патології того чи іншого органа застосовують графічний запис періодичних процесів, які супровод­жу­ють його функціональну діяльність, з подаль­шим його аналізом – визначенням його тривалості (періоду), частоти й амплітуди дослід­жуваних величин. Для розв’язан­ня подібних задач необхідне знання загальних закономір­ностей, що притаманні коливальним процесам незалежно від їх природи і що описуються єдиними математичними рівняннями. Закономірності, властиві коливальним проце­сам, най­більш просто вивчати на прикладі механічних коли­вань.

3.1.1. Гармонічні коливання та їх основні параметри

Розглянемо пружинний маятник (мал. 3.21). При змі­щен­ні матеріальної точки масою m на відстань х відносно положення рівно­ва­ги на неї починає діяти сила пружності, яка викликана дефор­мацією пружини

F_пр = – kх. (3.35)

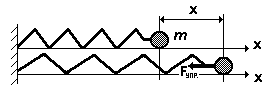
Мал. 3.21. Пружинний маятник.

Згідно з ІІ законом Ньютона ця сила надаватиме мате­ріаль­ній точці прискорення :

F_пр = ma. (3.36)

Прирівнюючи праві частини рівностей (3.35) і (3.36), одер­жи­мо:

ma = – kх. (3.37)

Враховуючи, що прискорення є другою похідною від координа­ти за часом , останнє рівняння набуває вигля­ду лінійного диференційного рівняння

. (3.38)

Оскільки коефіцієнт жорсткості пружини k > 0 і m > 0, відно­шен­ня k/m можна позначити через квадрат деякої величини : . Тоді рівняння (3.38) матиме вигляд:

. (3.39)

Таким чином, функція х = f (t) задовольняє диференцій­но­­му рів­нян­ню ІІ-го порядку, яке є лінійним, однорідним і зі сталими коефіцієнтами. Розв’язок таких рівнянь, як відомо, зводиться до розв’язування відповідних характеристичних алгебраїчних рівнянь.

Складемо характеристичне рівняння, що відповідає ди­фе­рен­цій­но­му рівнянню (3.39):

. (3.40)

Корені цього квадратного рівняння дорівнюють , тобто вони є різними й уявними.

Загальний розв’язок диференційного рівняння (3.39) на випадок таких коренів відповідного характеристичного рів­няння має вигляд:

.

Нехай c₁ = Асоs₀, a c₂ = – Asin₀, де A та ₀ – довільні сталі, тоді

. (3.41)

Якщо покласти c₁ = Аsin₀, a c₂ = Acos₀, то прийдемо до результату:

. (3.42)

Значення сталих А та ₀ визначаються початковими умовами, тоб­то положенням та швидкістю матеріальної точ­ки в момент часу t = 0.

Отже, ми дійшли до висновку: матеріальна точка, що знаходиться під дією пружної сили, здійснює коли­валь­ний рух, при якому її зміщення від положення рівноваги змінюється з часом за законом синуса або коси­нуса. Такі коливання називають гармонічними.

Стала А в рівняннях (3.42) є амплітуда гармонічного коливання, вона дорівнює максимальному зміщенню маят­ни­ка від положення рівноваги. Аргумент синуса (або коси­нуса): – фаза коливань. Фаза визначає змі­щен­ня маятника в будь-який момент часу, ₀ – початкова фаза, яка визначає зміщення маятника в момент часу t = 0. Величина – циклічна частота коливань.

Тій же самій закономірності підпорядковується зміщен­ня від положення рівноваги математичного маятника, що коливається, при невеликих кутах відхилення  (мал. 3.22).

Мал. 3.22. Математичний маятник.

Сила, яка спричиняє коливання математичного маятни­ка, не є пруж­на за своєю природою. Дійсно, повертаюча сила F спрямована по дотичній до дуги кола радіуса l, напрямлена до положення рівно­ваги і пропор­ційна зміщен­ню х:

F = – mgsin  – mg = – mg

(оскільки для малих кутів  маємо sin  tg  ).

Сила, що не є пружною за своєю природою, але анало­гічна їй по залежності від зміщення, називається квазіпруж­ною. Таким чином, F є квазіпружною силою. Рівняння дина­міки для матема­тич­ного маятника матиме вигляд:

, або , . (3.43)

Отримане рівняння повністю збігається з рівнянням (3.41), що описує рух пружного маятника, а отже має той самий розв’язок. Таким чином, гармонічні коливання – це коливання, що відбувають­ся під дією пружних або квазі­пружних сил.