Швидкість та прискорення при гармонічних коливаннях

Нехай відлік часу обрано таким чином, щоб початкова фаза ₀ = 0. Тоді розв’язок рівняння (3.41) матиме вигляд:

. (3.44)

Швидкість тіла, що коливається, знайдемо як похідну від координати х за часом t

, (3.45)

де – амплітуда швидкості.

З рівнянь (3.43) та (3.44) випливає, що швидкість також змінюється за гармонічним законом, а фаза швидкості від­різ­няється від фази зміщення на /2, тобто в момент часу, коли х = 0, швид­кість максимальна.

Оскільки швидкість при гармонічних коливаннях змі­ню­ється з часом, то цей рух характеризується прискорен­ням, яке знайдемо як другу похідну від зміщення х за часом

(3.46)

де – амплітуда прискорення.

Видно, що і прискорення змінюється за гармонічним законом, а фаза прискорення відрізняється від фази зміщен­ня на , а від фази швидкості на /2. Замінивши в (3.46) через x, отримаємо:

.

З цієї рівності виходить, що при гармонічних коливаннях прискорення тіла прямо пропорційне до зміщення від поло­ження рівноваги і має протилежний зміщенню напр­ямок.

Період і частота гармонічних коливань

Періодом гармонічного коливального руху називають наймен­ший проміжок часу Т, по закінченні якого всі вели­чини, що характеризують цей рух (х, υ, a), набувають пер­віс­ні значення. З рівностей (3.44) – (3.46) випливає, що пері­оду коливань відповідає зміна фази на величину 2.

У момент часу t фаза дорівнює , а в момент часу t + Т: . Тоді з умови періодичності маємо:

. (3.47)

Підставляючи в (3.47) вирази для ₀, що відповідають пружинному та математичному маятникам, отримаємо від­по­відні вирази для періодів коливань цих маятників:

, . (3.48)

Величину  = 1/Т = ₀/2 називають частотою коливань. Часто­та вказує, скільки разів за 1 сек повторюється один і той же стан тіла, що коливається. Частота вимірюється в Герцах (Гц), [] = 1/c = c^–1 = Гц.

Розглянуті коливання відбуваються при відсутності сил тертя і зовнішніх сил. Такі коливання називають власними. Частота (пері­од) власних коливань, як випливає з (3.48), залежить лише від властивостей самої системи.

3.3.2. Затухаючі коливання і аперіодичний рух

Припустимо, що в розглянутих системах існує тертя чи опір, причому сила тертя (опору) пропорційна швидкості: F_т = – rυ, де r – коефіцієнт тертя (опору). Запишемо в цьому випадку рівняння руху (ІІ закон Ньютона).

ma = – kх – rυ або .

Позначивши , , отримаємо диференційне рів­нян­ня другого порядку, що описує рух пружинного маят­ника у присутності сил тертя

. (3.49)

Складемо характеристичне рівняння, що відповідає ди­фе­рен­­цій­ному рівнянню (3.49):

.

Знайдемо корені характеристичного рівняння

. (3.50)

Зaгальний розв’язок рівняння (3.49) залежить від знака різниці . Розглянемо всі можливі випадки:

1. , коли корені характеристично­го рівняння є комплек­с­ни­ми числами (затухаючі коливання)

,

де – циклічна частота. У випадку комплексних коренів характеристичного рівняння загальний розв’я­зок (3.49) має вигляд

, або

, (3.51)

де – амплітуда коливань, яка зменшується за експо­ненці­ал­ьним законом,  – коефіцієнт затухання, визна­чає швидкість затухання амплітуди. Залежність х = f (t) для затухаючих коливань подано на мал. 3.23.

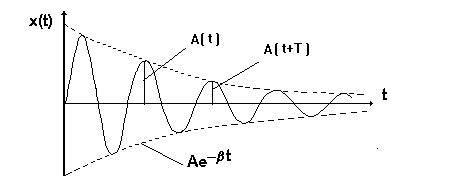
Мал. 3.23. Затухаючі коливання.

Ступінь затухання часто характеризують декрементом зату­хан­­­ня  і логарифмічним декрементом затухання ^:

,

,

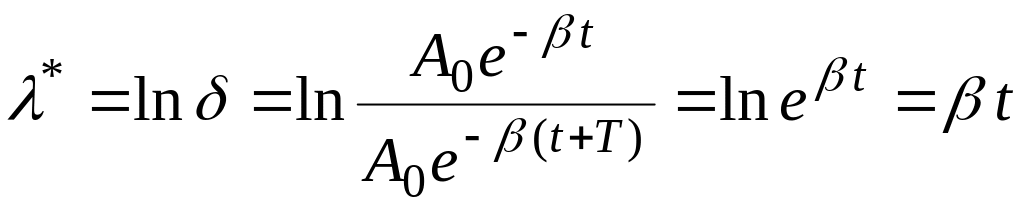де період затухаючих коливань дорівнює

.

2. , коли корені характеристично­го рівняння є дій­с­ни­ми числами (аперіодичні коливання)

.

У цьому випадку загальний розв’язок рівняння (3.49) ма­тиме вигляд

, (3.52)

що відповідає аперіодичному рухові (мал. 3.24).

3

Мал. 3.24. Аперіодичний рух.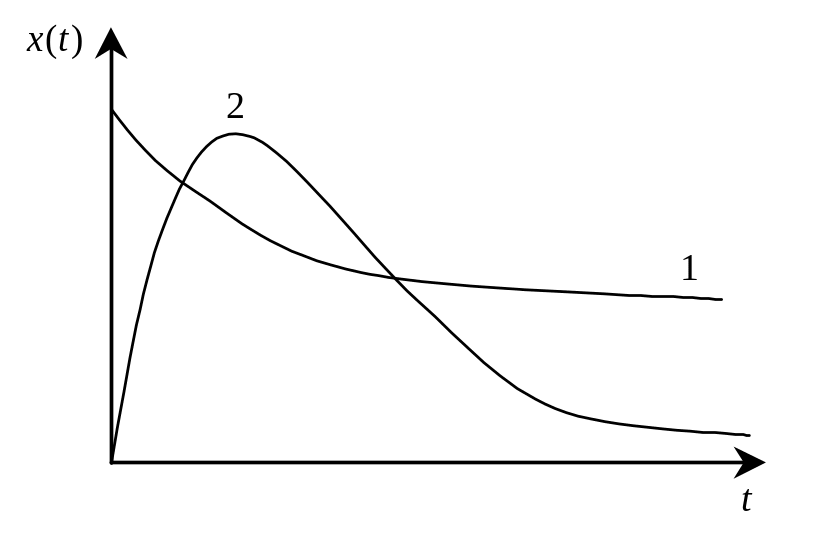

. , коли корені є кратними. Легко побачити, що і в цьому випадку рух тіла буде аперіодичним.

Коливання, що виника­ють у системі при відсут­нос­ті зовнішніх сил, нази­ва­ють вільними. Частота віль­них коливань залежить як від пружних власти­востей сис­те­ми (₀), так і від інтен­сив­ності втрат (). Якщо , то   ₀ і період вільних коливань стає близьким до періоду власних коливань (мал. 3.23).