Приклад розв’язку задачі 1 визначення реакцій опор балки
Горизонтальна
балка довжиною
м
встановлена на опорах
і
(рис. 1.7а) і навантажена зосередженою
силою
=15кН,
розподіленим навантаженням інтенсивністю
=20кН/м,
парою сил з моментом
=10кНм.
Не враховуючи силу ваги балки, визначити
реакції опор
і
.
Розв’язання
Відкинувши опори,
замінюємо їх реакціями (рис. 1.7б).
Розглядаємо рівновагу балки. Реакції
опор – це реактивні сили
і
.
Реактивні сили направимо вертикально,
оскільки активні сили, що діють на балку,
горизонтальних складових не мають.
Розподілене навантаження замінюємо
рівнодійною
.
Використовуючи умову рівноваги плоскої системи паралельних сил запишемо два рівняння рівноваги:
; 
;
; 
;
звіди визначимо невідомі реакції
кН;
кН.
Перевіримо розв’язок, склавши контрольне рівняння – суму проекцій всіх сил на вертикальну вісь
; 
.
Розв’язок вірний.
Рис. 1.7
а)
б)
Рис. 1.8
Приклад розв’язку задачі 2 визначення реакцій защемлення
Горизонтальна
балка (рис. 1.8а), що підтримує балкон,
піддається дії рівномірно розподіленого
навантаження інтенсивністю
кН/м.
На вільний кінець консолі (перетин С)
передається навантаження від колони
кН.
Відстань від осі колони до стіни (перетин
А)
м.
Визначити реакцію защемлення.
Розв’язання
Відкинувши
защемлення, замінюємо його реакціями
(рис. 1.8б). Розглядаємо рівновагу
балки. Реакція стіни – це реактивна
сила
і реактивний момент
.
Реактивна сила направлена вертикально,
оскільки активні сили, що діють на балку,
горизонтальних складових не мають.
Розподілене навантаження замінюємо
рівнодійною
.
Використовуючи умову рівноваги плоскої системи паралельних сил запишемо два рівняння рівноваги:
; 
;
звідки 
кН;
; 
;
звідки 
Нм.
Перевіримо розв’язок, склавши контрольне рівняння моментів відносно точки
; 
.
Підставивши значення, одержимо
.
Розв’язок вірний.
Примітка.
Для схем, заданих в умові задачі 2, при
складанні рівняння рівноваги для
визначення реактивного моменту, вираз
моменту від розподіленого навантаження
записують як
.
2. Центральний розтяг-стиск
Розтяг (стиск) – це такий вид деформації, при якому в поперечних перетинах бруса виникає тільки нормальна сила – N.
Нормальна сила додатна, якщо розтягує матеріал бруса; від’ємна – стискає. Брус, що працює на розтяг (стиск) називається стержнем.
Для оцінки навантаженості бруса будують епюри. Епюра – це графік, який показує розподіл внутрішніх силових факторів або переміщень вздовж осі бруса. Епюри штрихують лініями перпендикулярними до осі.
При побудові епюр використовуємо метод перетинів.
Приклад: Побудувати епюру нормальних сил для заданого бруса показаного на рис. 2.1а (власною вагою нехтуємо).
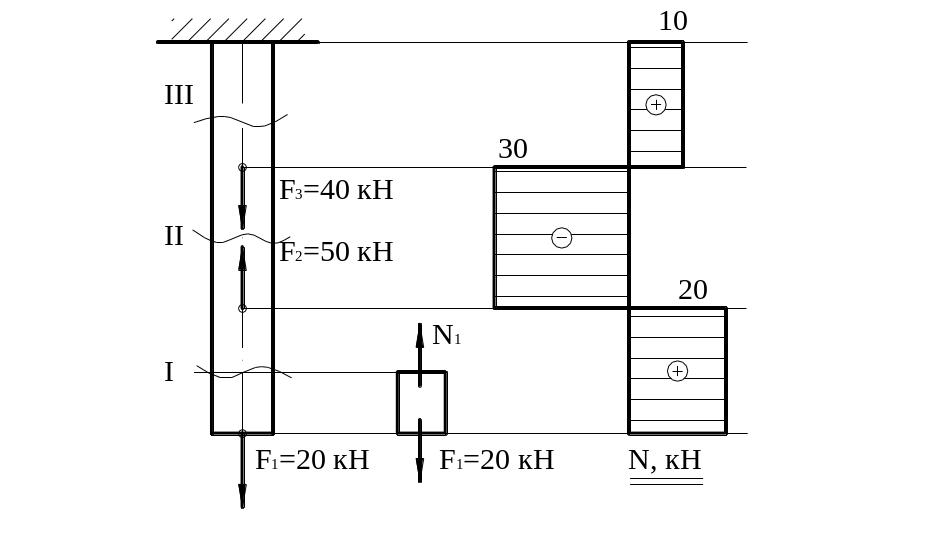
Рис. 2.1
Розв’язання
Розбиваємо брус на ділянки.
Використовуючи метод перетинів визначаємо значення нормальних сил на кожній ділянці, починаючи від вільного кінця.
Нормальна сила – це алгебраїчна сума всіх зовнішніх сил, що знаходяться з одного боку перетину. Запишемо їх значення:
За отриманими результатами будуємо епюру нормальних сил N, (рис. 2.1б).
Між нормальною силою N і нормальним напруженням σ існує залежність, рис. 2.2. Вважаємо, що σ=const , тоді N = σ ∙A, або σ=N/A.
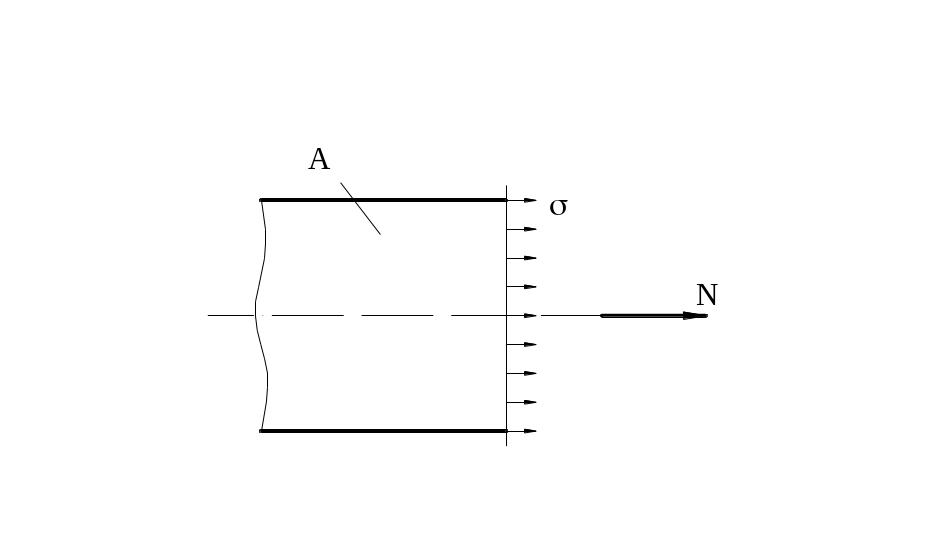
Рис. 2.2