1.2. Векторный способ задания движения, определение скорости точки

Положение точки в пространстве однозначно определяется заданием радиуса-вектора, проведенного из некоторого неподвижного центра О в данную точку М (рис. 2.2). Для определения движения точки должна быть задана вектор-функция аргумента t

.

При векторном способе задания движения положение движущейся точки в каждый момент времени (рис. 2.3) определяется радиусом-вектором. Вектор скорости точки в данный момент равен производной от радиуса-вектора точки по времени.

.

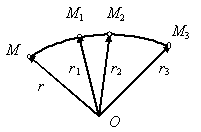
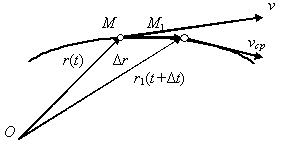
Рис. 2.2 Рис. 2.3

Вектор скорости точки направлен по касательной к траектории в сторону движения точки. При движении точки по криволинейной траектории направление вектора скорости непрерывно изменяется (рис. 2.4).

Рис. 2.4

1.3. Координатный способ задания движения точки, определение скорости точки

Положение точки М в системе отсчета Охуz определяется тремя декартовыми координатами точки х, у, z (рис. 2.5). При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, у, z движущейся точки М являются функциями времени t:

.

Эти уравнения называются уравнениями движения точки в декарто­вых координатах.

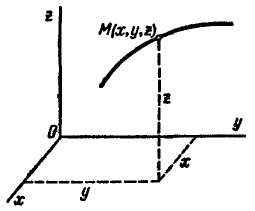
Рис. 2.5

Движение точки М в одной плоскости определяется двумя урав­нениями движения (рис. 2.6, а):

.

а) б)

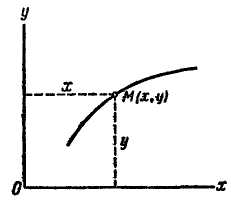
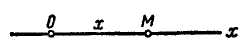
Рис. 2.6

Прямолинейное движение точки М определяется одним уравнением движения (рис. 2.6, б)

.

Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматривать как параметрические уравнения траектории точки, а время – как независимый переменный параметр. При исключении параметра t из уравнений движе­ния получаются уравнения траектории точки в координатной форме. Пусть уравнения движения точки М имеют вид

Решив первое уравнение относительно t, получим

Подставив полученное для t выражение в два других уравнения, найдем уравнения траектории точки в координатной форме:

Два уравнения с тремя координатами определяют линию в пространстве, т.е. траекторию точки. Пусть движение точки М в плоскости задано уравнениями

Исключив параметр t, получим уравнение траектории точки в коор­динатной форме:

Помимо декартовых координат для определения положения точки на плоскости и в пространстве применяют и другие системы коор­динат (полярные, цилиндрические, сферические и др.).

Определим модуль и направление скорости точки по уравнениям ее движения в декартовых координатах (рис. 2.7).

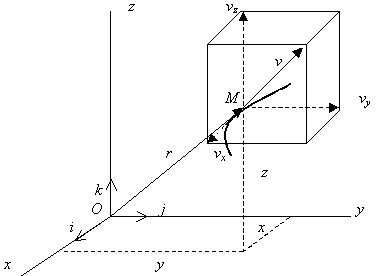
Рис. 2.7

.

Проекции скорости точки на неподвижные оси де­картовых координат равны первым производным от соответствующих координат точки по времени.

Вычислив проекции скорости на оси декартовых координат, можно определить модуль и направление скорости точки по следующим формулам:

.

Движение точки в плоскости хОу задается двумя урав­нениями движения. Модуль и направление скорости точки в этом случае определяются так:

.

Прямолинейное движение точки задается одним уравнением. В этом случае модуль скорости точки равен абсолютной величине проекции скорости на ось х:

.

При точка движется по направлению оси х, при - противоположно направлению оси.

Задача 2.1. Кривошип ON длиною а вращается вокруг оси, перпендикулярной к плоскости рисунка и проходящей через точку О. Угол φ между неподвижной осью Ох и кривошипом изменяется пропорционально времени: φ=kt. Составить уравнения движения точки N в декартовой системе координат. Найти уравнения ее траектории (рис. 2.8).

Решение. Для составления уравнений движения точки N надо выразить ее координаты как функции времени. Из рисунка находим координаты x,y точки N:

; (2.1)

. (2.2)

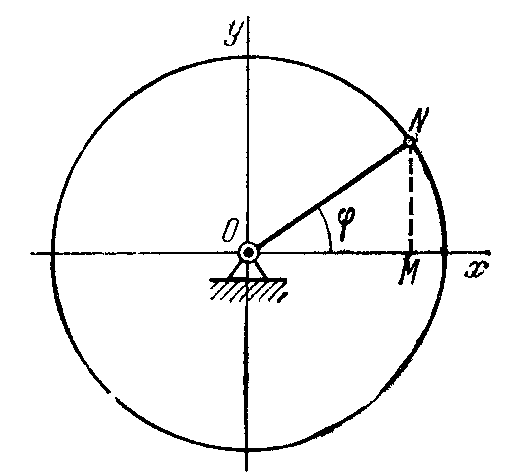
Рис. 2.8

Это и будут искомые уравнения движения точки N.

Чтобы найти уравнение траектории точки в явной форме, надо исключить из уравнений движения время. Для этого возведем каждое уравнение движения (2.1 и 2.2) в квадрат

; (2.3)

  (2.4)

и сложим уравнения (2.3) и (2.4):

.

Это уравнение траектории точки N - уравнение окружности радиусом а с центром в начале координат.