рад/с.

Подставляя в (а), получим:

м/с.

Вектор переносной скорости изобразим перпендикулярно радиусу переносного вращения в сторону (рис. 2.108).

Для определения направления абсолютной скорости сложим векторы составляющих скоростей по правилу параллелограмма, а модуль определим по формуле

3. Определение абсолютного ускорения . Так как переносное движение поступательное, то воспользуемся теоремой Кориолиса

.

Относительное ускорение можно определить по зависимости

,

где м/с².

На рис. 2.109 изобразим , направив вектор от точки М к центру окружности.

Переносное ускорение определится по формуле

,

где

м/с².

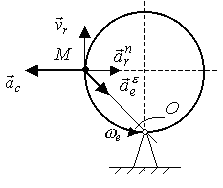
Рис. 2.109

Вектор имеет начало в точке М и направлен вдоль радиуса переносного вращения ОМ к центру О.

Ускорение Кориолиса равно

.

Вектор угловой скорости направлен вдоль оси вращения,т.е. вдоль прямой, перпендикулярной плоскости чертежа, а вектор относительной скорости лежит в плоскости чертежа, т.е. в любой момент времени угол между и равен , а . Поэтому

м/с².

Для показа воспользуемся правилом Жуковского. Так как уже находится в плоскости, перпендикулярной оси переносного вращения, повернем его на 90^о в сторону , т.е. против хода часовой стрелки.

Модуль абсолютного ускорения определим по методу проекций:

;

м/с²,

отсюда

м/с².

7.5. Сложение вращений твердого тела вокруг двух параллельных осей

Пусть твердое тело вращается вокруг оси Оz (рис. 2.110) с относительной угловой скоростью (относительное движение по отношению к осям Oxyz), а система осей Oxyz вращается вокруг оси O₁z₁ параллельной оси Оz с переносной угловой скоростью (переносное движение по отношению к осям O₁x₁y₁z₁).

Если провести плоскость Q перпендикулярную осям вращения Оz и O₁z₁, то в сечении твердого тела получим плоскую фигуру, которая в относительном и переносном движениях будет оставаться в плоскости сечения. Это означает, что и в абсолютном движении плоская фигура остается в плоскости сечения.

Следовательно, результирующим (абсолютным) движением твердого тела будет плоское и характеризуется движением плоской фигуры в ее плоскости. Рассмотрим три случая.

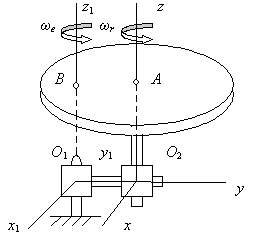
Рис. 2.110

С л у ч а й 1. Переносное и относительное вращения направлены в одну сторону.

Изобразим сечение твердого тела плоскостью Q, перпендикулярной осям Oz и . Следы осей в сечении обозначим А и В (рис. 2.111).

Точка А плоской фигуры в относительном вращении имеет скорость равную 0, в переносном

.

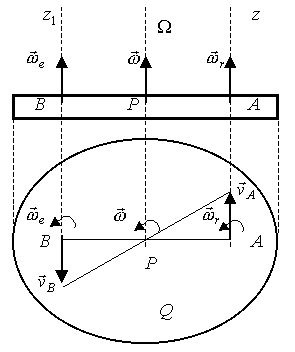
Рис. 2.111

Точка В плоской фигуры в переносном вращении имеет скорость равную 0, а в относительном

.

Векторы и параллельны.

Мгновенный центр скоростей Р найдем на пересечении отрезков, соединяющих точки А и В и концы векторов скоростей этих точек.

Мгновенная ось абсолютного вращения проходит через мгно­венный центр скоростей Р.

Таким образом, мгновенная ось абсолютного вращения плоской фигуры лежит в плоскости, проходящей через оси переносного и отно­сительного вращений, и, будучи параллельной им, делит расстояние между этими осями на части, обратно пропорциональные угловым скоростям.

.

Итак, если тело участвует одновременно в двух направленных в одну сторону вращениях вокруг параллельных осей, то результирующим (абсолютным) движением будет вращение вокруг мгновенной оси, параллельной данным, с модулем абсолютной угловой скорости, равным сумме модулей угло­вых скоростей составляющих вращений.

.

С течением времени мгновенная ось меняет свое положение, описывая цилиндрическую поверхность. Положение мгновенной оси определяется соотношением

,

где ВР и АР – расстояния от данных осей вращения до мгновенной; АВ – расстояние между данными осями.

Задача 2.24. Кривошип О₁О (рис. 2.112) вращается вокруг неподвижной оси Oz против хода часовой стрелки с угловой скоростью и заставляет подвижную шестерню 2 радиуса r₂ катиться по неподвижной шестерне 1 радиуса r₁. Определить абсолютную и относительную угловые скорости шестерни 2.

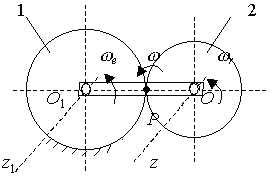
Рис. 2.112

Решение. Рассмотрим простейшую цилиндрическую планетарную передачу. Мгновенный центр скоростей шестерни 2 находится в точке касания шестерен. Для шестерни 2 вращение кривошипа является переносным, угловая скорость - переносной, а ось Oz₁ – осью переносного вращения. Ось относительного вращения шестерни 2 – Oz, мгновенная ось абсолютного вращения проходит через точку Р, перпендикулярную плоскости движения.

Для определения относительной скорости запишем

,

тогда .

Абсолютная угловая скорость

.

С л у ч а й II. Переносное и относительное вращения направлены в разные стороны, а модули их угловых скоростей не равны.

Изобразим сечение твердого тела плоскостью, перпендикулярной осям вращения Oz и . Скорость направим в противоположную сторону и для определенности будем полагать (рис. 2.113).

Выразим скорости точек А и В через формулы

и покажем на рисунке.

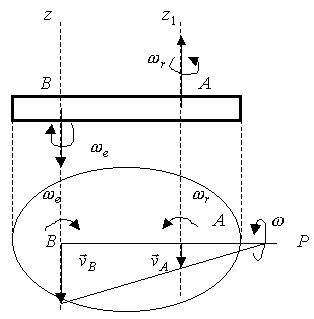
Рис. 2.113

Мгновенный центр скоростей Р находится на пересечении продолжения отрезка АВ и отрезка, соединяющего концы векторов скоростей и . Через точку Р пройдет мгновенная ось вращения, которая будет параллельна данным осям. Абсолютная угловая скорость равна

.

Таким образом, если твердое тело участвует в двух направленных в разные стороны вращениях вокруг параллельных осей, то мгновенная ось абсолютного вращения плоской фигуры параллельна осям переносного и относительного вращений и лежит в плоскости, проходящей через эти оси, со стороны той оси, угловая скорость вращения вокруг которой больше.

С течением времени мгновенная ось вращения меняет свое положение, описывая цилиндрическую поверхность. Положение оси определяется соотношениями

.

Задача 2.25. Кривошип О₁О вращается вокруг неподвижной оси О₁z₁ против хода часовой стрелки (рис. 2.114) с угловой скоростью и заставляет подвижную шестерню 2 радиуса r₂ катиться по неподвижной шестерне 1 радиуса r₁. Определить абсолютную и относительную скорости шестерни 2.

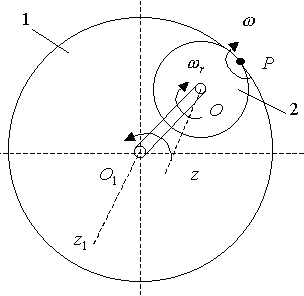
Рис. 2.114

Решение. Мгновенный центр скоростей шестерни 2 находится в точке касания шестерен, т.е. на продолжении отрезка, соединяющего точки О и О₁. запишем соотношение

,

откуда

.

Известно, что при внутреннем зацеплении угловые скорости шестерен направлены в разные стороны, значит направлена по ходу часовой стрелки, т.е. .

Для определения абсолютной угловой скорости запишем равенство

.

Знак минус в ответе означает, что абсолютная угловая скорость направлена в сторону, противоположную .

Задача 2.26. Определить угловые скорости колес цилиндрического редуктора (рис. 2.115). Исходные данные: радиусы колес , , см; угловые скорости об/мин, об/мин.

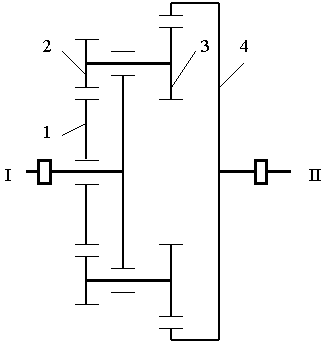
Рис. 2.115

Решение. 1) Решение задачи способом Виллиса. Этот способ позволяет определять угловые скорости звеньев механизма, участвующих в двух вращениях: переносном и относительном.

Колеса редуктора участвуют: в относительном вращении (по отношению к водилу) вокруг собственной оси; в переносном вращении вместе с водилом вокруг его оси.

Переносной угловой скоростью для каждого колеса является угловая скорость водила . Относительные угловые скорости колес определяются как разности абсолютных и переносных угловых скоростей:

……………….

.

Эти относительные скорости являются угловыми скоростями всех колес при мысленно остановленном водиле. В этом случае между относительными угловыми скоростями имеются такие же соотношения, как в зубчатых передачах с неподвижными осями вращений. Следовательно,

,

где т – число внешних зацеплений между колесами; i – передаточное число от колеса 1 к колесу I в относительном движении (при остановленном водиле).

Это соотношение носит название формулы Виллиса. В эту формулу входят алгебраические значения угловых скоростей. Знак «+» примем соответствующим вращении против часовой стрелки, а «–» – вращению по часовой стрелке. В формулу Виллиса вместо можно подставить п об/мин.

Применим формулу Виллиса к решению рассматриваемой задачи (рис. 2.116, а). Так как колеса 1 и 2 находятся во внешнем зацеплении, а колеса 3 и 4 – во внутреннем и угловая скорость вращения водила равна , то

,

откуда .

а)

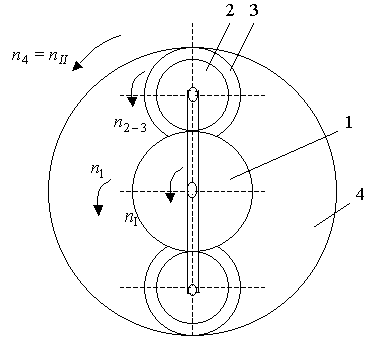
б)

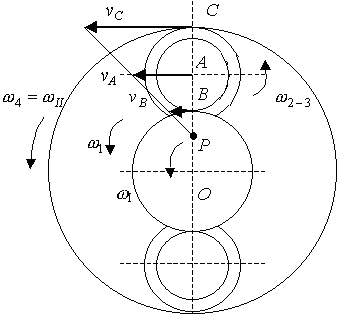
Рис. 2.116

Подставляя сюда числовые значения, находим

об/мин.

Знак «+» в ответе указывает, что вал II вращается в направлении, противоположном вращению часовой стрелки.

Угловую скорость шестерен 2 и 3 (сателлитов) определяем из следующего соотношения:

,

откуда

.

Подставляя сюда числовые значения, находим:

об/мин.

2) Решение задачи способом мгновенных центров скоростей. По угловым скоростям ведущих звеньев найдем скорость точки А оси спаренных шестерен и скорость точки В касания колес 1 и 2.

; ;

см/с;

см/с.

Отложив векторы и (рис. 2.116, б), найдем мгновенный центр скоростей шестерен 2 и 3:

.

Так как

см,

то

.

Затем определяем скорость точки С:

см/с.

По скорости точки А или В находим угловые скорости шестерен 2 и 3:

;

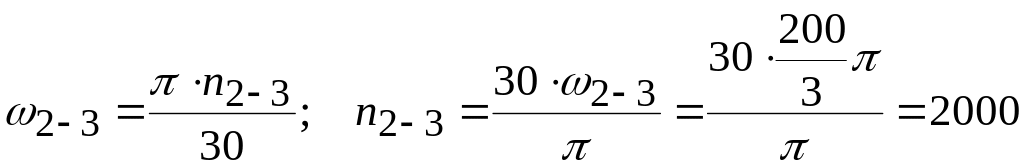об/мин.

По скорости точки С находим угловую скорость колеса 4:

об/мин;

об/мин.

С л у ч а й III. Переносное и относительное вращения направлены в разные стороны, а модули их угловых скоростей равны (пара вращений).

Изобразим сечение тела (рис. 2.117), совершающего сложное движение. Скорости точек А и В сечения будут равны:

,

но так как , то .

Это означает, что мгновенный центр скоростей находится в бесконечности, и все точки тела в данный момент времени имеют геометрически равные скорости

.

Результирующим движением в этом случае будет поступательное движение со скоростью равной и направленной перпендикулярно плоскости, соединяющей и . Такие совокупности вращений называются парой вращений, а векторы и образуют пару угловых скоростей.

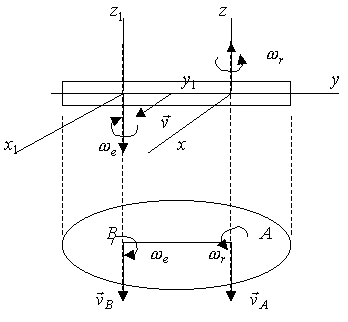
Рис. 2.117

Пара вращений эквивалентна поступательному движению со скоростью , равной моменту пары угловых скоростей этих вращений.

Задача 2.27. Шестерня 4 планетарного зубчатого механизма, изображенного на рис. 2.118, а, свободно укреплена на конце рукоятки ОА, которая вращается вокруг оси О неподвижной шестерни 1 с постоянной угловой скоростью в сторону, обратную вращению часовой стрелки. На рукоятке ОА лежит ось двойной шестерни 2-3, находящейся в зацеплении с шестернями 1 и 4; числа зубьев шестерен соответственно равны . Определить угловую скорости шестерни 4.

Решение. Примем вращение рукоятки ОА вокруг оси О за переносное вращение и найдем угловые скорости относительных вращений шестерен по отношению к рукоятке (рис. 2.118, 6). Относительное вращение неподвижной ше­стерни 1 происходит вокруг оси О навстречу вращению рукоятки с угловой скоростью, модуль которой равен модулю угловой скорости рукоятки

.

Направления относительных вращений двойной шестерни 2-3 и шестерни 4 показаны на рис. 2.118, б.

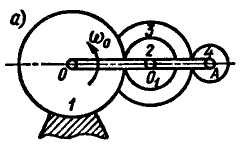
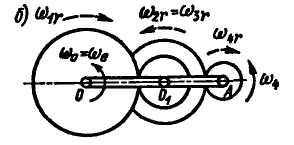
Рис. 2.118

Модули относительных угловых скоростей шестерен обратно пропорцио­нальны числам их зубьев, т. е.

; (а)

. (б)

Шестерни 2 и 3 связаны между собой жестко, а поэтому .

Перемножая (а) и (б), получаем:

,

откуда

.

Так как переносное и относительное вращения шестерни 4 направлены противоположно, то, полагая , найдем , как разность модулей ее переносной и относительной угловых скоростей:

,

откуда

.

На рис. 2.118, б абсолютное вращение шестерни 4 направлено в сторону переносного вращения, так как положено , т.е.

или .

В случае направление абсолютного вращения шестерни 4 про­тивоположно указанному.