2.2. Свободные колебания материальной точки без учета сопротивления

Колебательное движение материальной точки происходит при условии, если на точку М, отклоненную от положения покоя О (рис. 3.15), действует восстанавливающая сила.

Рис. 3.15

Дифференциальное уравнение прямолинейного движения точки М под действием восстанавливающей силы P

или .

Обозначим ,

. (3.1)

Уравнение (3.1) называется дифференциальным уравнением свободных колебаний материальной точки. Его решением будет:

.

С учетом начальных условий движения при , получим:

.

Обозначим

.

С учетом этого дифференциальное уравнение (3.1) примет вид:

. (3.2)

где А – амплитуда колебаний; - фаза колебаний; - начальная фаза колебаний.

Из уравнения (3.2) видно, что отклонения материальной точки от положения равновесия подчиняются гармоническому закону. Такие колебания называются гармоническими (рис. 3.16).

Рис. 3.16

Амплитуда свободных колебаний – наибольшее отклонение точки от положения равновесия – определяется по зависимости

.

Фаза свободных колебаний

.

;

.

Циклическая частота (частота) колебаний

.

Период свободных колебаний

.

2.3. Математический маятник и его малые колебания

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая движение в одной вертикальной плоскости под действием cuлы тяжести (рис. 3.17).

Рис. 3.17

Дифференциальное уравнение движения математического маятника

Это дифференциальное уравнение соответствует гармоническому колебательному движению.

Если обозначить

то получим следующее дифференциальное уравнение:

Решение этого уравнения имеет вид:

или

,

где а — амплитуда угла φ при малых колебаниях маятника.

Величина амплитуды зависит от начальных условий движения маятника. Период малых колебаний маятника определится по частоте колебаний k

, т. е. .

2.4. Затухающие свободные колебания материальной точки

Затухающие свободные колебания, где кроме восстанавливающей силы, направленной к центру колебаний, на точку действует сила сопротивления, направленная всегда в сторону, противоположную направлению движения точки (рис. 3.18).

Рис. 3.18

Модуль силы сопротивления среды R пропорционален модулю скорости точки

.

Если v = 1, то R = α, т.е. коэффициент пропорциональности α численно равен силе сопротивления при скорости движения точки, равной единице. Сила сопротивления R направлена всегда противоположно скорости точки .

Проекции силы сопротивления и скорости точки на ось х имеют противоположные знаки

.

Дифференциальное уравнение движения материальной точки:

или .

Введем обозначения и , тогда

. (3.3)

Уравнение (3.3) является дифференциальным уравнением движения материальной точки под действием восстанавливающей силы и силы сопротивления, пропорциональной скорости точки.

Общее решение уравнения (3.3) имеет вид:

, (3.4)

где .

Подставив в уравнение (3.4) значения постоянных интегрирования и , получим:

. (3.5)

Движение, определяемое уравнением (3.5), имеет колебательный характер, так как координата х периодически изменяет свой знак при изменении знака, входящего в уравнение синуса. Множитель указывает на то, что амплитуда колебаний с течением времени уменьшается. Колебания этого вида называются затухающими. Так как , то абсолютная величина координаты х удовлетворяет условию

.

Следовательно, график затухающих колебаний (рис. 3.19) заключен между двумя симметричными относительно оси абсцисс кривыми, имеющими уравнения

и .

Амплитуда этих колебаний

,

где п – коэффициент затухания.

Рис. 3.19

При t = 0 начальное значение амплитуды

.

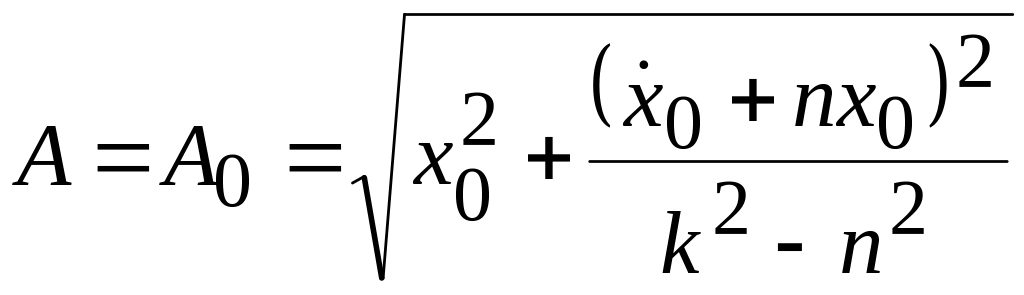Начальная фаза колебаний

; ; .