10.3. Центр тяжести твердого тела

Обозначим силы притяжения отдельных элементарных частиц тела к Земле , вес тела G, координаты (рис. 1.100) его центра тяжести , а координаты любой частицы твердого тела . Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил.

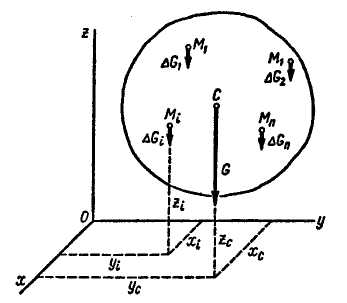
Рис. 1.100

Для центра тяжести формулы примут вид

где суммирования распространены на все частицы твердого тела. В этих формулах алгебраическими величинами являются только координаты точек, а значения всегда положительны, так как все силы направлены в одну сторону.

Определим положение центра тяжести однородного тела.

Вес однородного тела определяется формулой , где V- объем тела, γ - вес единицы объема. Тогда

.

Центр тяжести однородного тела, заполняющего некоторый объем, называется центром тяжести этого объема.

10.4. Центр тяжести плоской фигуры. Статический момент площади плоской фигуры относительно оси

Положение центра тяжести плоской фигуры определяется двумя координатами и (рис. 1.101). Таким образом,

где суммирования распространены на все элементы площади. Центр тяжести однородной пластинки называют центром тяжести площади этой пластинки.

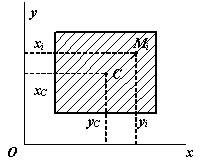
Рис. 1.101

Сумма произведений элементарных площадей, входящих в состав площади фигуры, на алгебраические значения их расстояний до некото­рой оси называется статическим моментом площади плоской фигуры относительно этой оси. Обозначая и статические моменты площади плоской фигуры относительно осей х и у, имеем:

.

Таким образом, статический момент площади плоской фигуры относительно оси равен произведению пло­щади фигуры на алгебраическое значение расстояния от центра тяжести до этой оси.

Если известны статические моменты площади плоской фигуры относительно координатных осей, то координаты ее центра тяжести можно определить по фор­мулам:

.

Очевидно, что статический момент площади плоской фигуры отно­сительно оси, проходящей через центр тяжести фигуры, равен нулю.

10.5. Вспомогательные теоремы для определения положения центра тяжести

Теорема 1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси (рис. 1.102).

Применяя эту теорему к плоской фигуре или линии, легко уста­новить, что если плоская фигура или линия имеет ось симметрии, то ее центр тяжести лежит на этой оси.

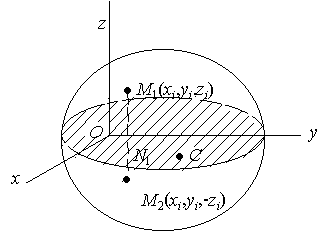
Рис. 1.102 Рис. 1.103

Теорема 2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости (рис. 1.103). На основе рассмотренных теорем можно определить положения центров тяжести некоторых симметричных линий, фигур и тел:

1) центр тяжести отрезка прямой лежит в его середине;

2) центры тяжести окружности, площади круга, поверхности и объема шара находятся в их геометрических центрах;

3) центры тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения их диагоналей;

4) центр тяжести периметра и площади правильного многоуголь­ника находится в центре вписанного (или описанного) круга.

Теорема 3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описан­ной ее центром тяжести (рис. 1.104).

,

где - длина окружности, описанной центром тяжести фигуры; F – площадь фигуры вращения.

Теорема 4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести (рис. 1.105).

,

где - длина окружности, описанной центром тяжести фигуры; L – длина плоской кривой вращения.

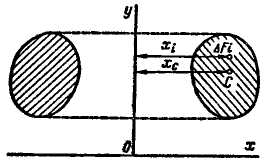
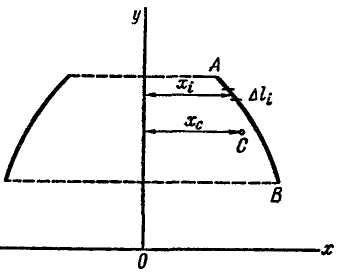
Рис. 1.104 Рис. 1.105