2.4. Ускорение точки при задании ее движения координатным способом

Определим модуль и направление ускорения точки по уравнениям ее движения в декартовых координатах. Пусть заданы уравнения движения точки (рис. 2.14)

Рис. 2.14

Проекции ускорения на оси координат определяются по формулам:

.

Так как первые производные от координат точки по времени равны проекциям скорости на соответствующие оси, т.е.

то проекции ускорения точки можно представить в другом виде:

Следовательно, проекции ускорения точки на неподвижные оси декартовых координат равны вторым производным от соответствую­щих координат точки по времени или первым производным по времени от проекций скорости на соответствующие оси.

После вычисления проекций ускорения на координатные оси можно опре­делить модуль и направление ускорения точки:

Движение точки в плос­кости хОу задается двумя уравнениями движения:

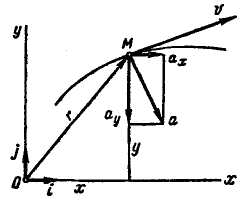
Рис. 2.15

Модуль и направление ускорения точки в этом случае (рис. 2.15) опреде­ляются так:

Прямолинейное движение точки задается одним уравнением x=f(t). В этом случае модуль ускорения равен абсолютному значению его проекции на ось х, т. е.

Ускорение направлено в сторону оси х, если , и противоположно оси х, если .

2.5. Определение радиуса кривизны траектории при координатном способе задания движения

Касательное ускорение точки возможно лишь при неравномерном движении точки и характеризует изменение модуля скорости.

В том случае, если требуется определить касательное и нормаль­ное ускорения движения точки, которое задано уравнениями движения , то сначала определяют модули скорости и ускорения точки:

Согласно формуле

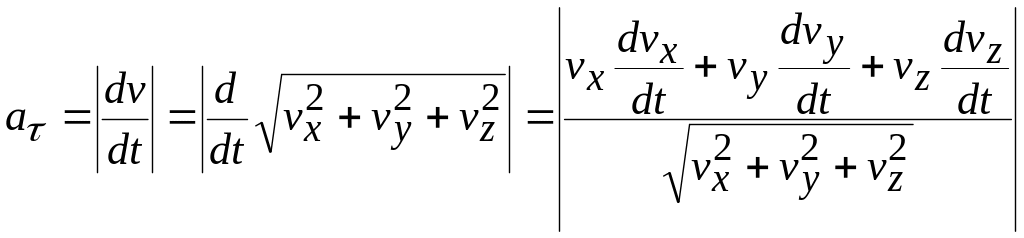
или

где знак плюс, полученный в ответе после вычисления дроби соответствует ускоренному движению точки, а знак минус - замедленному.

С другой стороны, модуль ускорения точки равен

,

тогда

Зная, что ,

находим радиус кривизны кривой по формуле

2.6. Классификация движения точки по ускорениям ее движения

Равномерное движение.

Выясним зависимость характера движения точки от значений ее нормального и касательного ускорений.

С л у ч а й I: Если в течение некоторого промежутка времени нормальное и касательное ускорения точки равны нулю, то в течение этого промежутка не изменяются ни направление, ни модуль скорости, т.е. точка движется равномерно-прямолинейно и ее уско­рение равно нулю.

С л у ч а й II: . Если в течение некоторого проме­жутка времени не равно нулю нормальное ускорение и равно нулю касательное ускорение, то происходит изменение направления скорости без изменения ее модуля, т. е. точка движется равномерно-криволинейно и модуль ее ускорения (рис. 2.16)

.

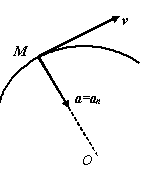
Рис. 2.16

Если в некоторый момент времени, то точка не движется равномерно, а в этот момент времени модуль ее скорости имеет максимум, или минимум.

Уравнение равномерного движения точки имеет вид

.

Постоянную скорость равномерного движения точки можно определить из уравнения движения

.

Графики равномерного движения и его скорости представлены на рис. 2.17.

Рис. 2.17

Равнопеременное движение. При равнопеременном движении алгебраическое значение касательного ускорения остается во все время движения неизменным .

С л у ч а й III: . Если в течение некоторого проме­жутка времени равно нулю нормальное ускорение точки и не равно нулю касательное, то направление скорости не изменяется, а изменя­ется ее модуль, т.е. точка движется по прямой неравномерно. Модуль ускорения точки в этом случае (рис. 2.18)

а) Ускоренное движение б) Замедленное движение

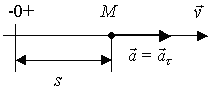
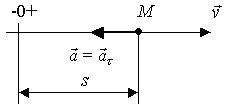
Рис. 2.18

С л у ч а й IV: . Если в течение некоторого проме­жутка времени ни нормальное, ни касательное ускорения точки не равны нулю, то изменяется как направление, так и модуль ее ско­рости, т. е. точка совершает неравномерно-криволинейное движение. Модуль ускорения точки

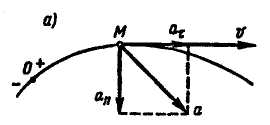
Рис. 2.19

Графическое изображение ускорения точки при равнопеременном криволинейном движении представлено на рисунке 2.19, а ускоренного движения, рис. 2.19, б – замедленного движения.

Уравнение равнопеременного движения точки имеет вид

Если , то при ускоренном движении , а при замедленном движении . Формула скорости равнопеременного движения точки имеет вид

.

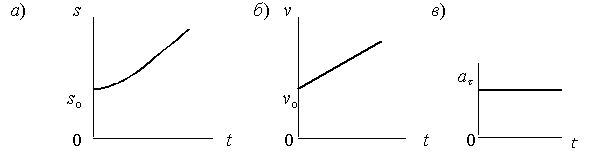
– ускоренное движение

Рис. 2.20

Графики замедленного движения, скорости и касательного ускорения представлены на рис. 2.21.

–- замедленное движение

Рис. 2.21

Задача 2.2. Определить траекторию, скорость и ускорение точки М шатуна кривошипно-ползунного механизма (рис. 2.22), если ОА=АВ=2b, а угол при вращении кривошипа растет пропорционально времени .

Рис. 2.22

Решение. Начинаем с определения уравнений движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у, находим:

.

Заменяя его значением, получаем уравнения движения точки М:

.

Для определения траектории точки М представим уравнения движения в виде:

.

Возводя эти равенства в квадрат и складывая, получим

.

Итак, траектория точки М — эллипс с полуосями 3b и b.

Теперь находим скорость точки М:

.

Скорость оказывается величиной переменной, изменяющейся с течением времени в пределах от до .

Определяем проекции ускорения точки М:

отсюда

,

где r — длина радиуса-вектора, проведенного из центра О до точки М. Следо­вательно, модуль ускорения точки меняется пропорционально ее расстоянию от центра эллипса.

Направление ускорения определяем по направляющим косинусам:

.

Ускорение точки М все время направлено вдоль МО к центру эллипса.

Задача 2.3. Локомотив движется равномерно по закруглению радиусом R = 600 м, причем ускорение его центра тяжести равно а = 0,26 м/с².

Определить скорость центра тяжести локомотива.

Решение. По условию задачи необходимо определить скорость центра тяжести локомотива, т.е. задача сводится к кинематике точки. Движение точки задано естественным способом, так как известна траектория движения. Покажем на рис. 2.23 траекторию – дугу радиусом R, на ней выберем начало и положительное направление отсчета дуговой координаты s.

Рис. 2.23

При естественном способе задания движения ускорение точки равно

.

В случае равномерного движения . Тогда , но

,

где - радиус кривизны траектории в данной ее точке. В нашем случае = 600 м в любой точке траектории.

Окончательно имеем

м/с.

На рис. 2.23 в произвольном положении точки изображены ее вектор скорости, направленный в сторону возрастания дуговой координаты, и ускорение, равное нормальному ускорению и направленному к центру кривизны траектории.

Задача 2.4. По заданным уравнениям движения точки М установить вид ее траектории и для момента времени , найти положение точки на траектории, ее скорость, касательное, нормальное и полное ускорения, а также радиус кривизны траектории (рис. 2.24):

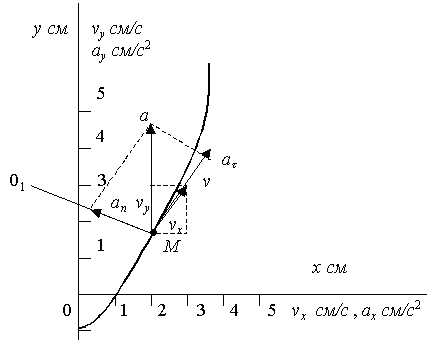
Рис. 2.24

, (2.5)

где х и у в сантиметрах, t – в секундах.

Решение. Параметрическим представлением траектории является сам закон движения. Уравнение траектории в координатной форме получаем, исключая из закона движения время:

.

Получили , то есть траекторией точки является парабола. Для построения траектории рассчитаем по уравнениям координаты точек параболы, отвечающие нескольким моментам времени. Результаты расчетов приведены в табл. 2.1.

Таблица 2.1

t, с	0	0,5	1
х, cм	0	2	4
у, см	- 1	1	7

Траектория построена на рис. 2.24, на ней стрелкой показано направление движения точки из начального положения при с координатами .

Дифференцируя (2.5) по времени, находим проекции скорости точки на оси координат х, у:

. (2.6)

При .

По найденным проекциям определяем модуль скорости

.

Дифференцируя (2.6), находим проекции вектора ускорения

.

При .

По найденным проекциям определяем модуль ускорения

.

Определение касательного ускорения при

.

Определение нормального ускорения при

.

Определение радиуса кривизны при

.

Результаты вычислений для заданного момента времени приведены в табл. 2.2.

Таблица 2.2

Координаты, см		С к о р о с т ь, см/с			Ус к о р е н и е, см/с2					Радиус кривизны, см
х	у	vx	vy	v	ax	ay	a	a	an	
2	1	4	8	8,9	0	16	16	14,4	6,9	11,6

На рис. 2.24 показано положение точки М в заданный момент времени.

Векторы скорости и ускорения точки М построены в масштабе по их проекциям на оси координат: , там же показаны касательное и нормальное ускорения. Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.

Радиус кривизны проведен в сторону вогнутости траектории перпендикулярно к вектору скорости – по направлению .

Таблица 2.3