Глава 2. Ускорения точки при различных способах задания движения

2.1. Ускорение точки при задании ее движения

Векторным способом

Ускорение точки характеризует быстроту изменения модуля и направления скорости точки (рис. 2.9). Размерность ускорения , т.е. единицы длина/время².

Вектор ускорения точки равен первой производной от скорости или второй производной от радиуса-вектора точки по времени.

.

Рис. 2.9

Вектор ускорения точки расположен в плоскости кривой, являющейся траекторией точки и направлен в сторону ее вогнутости.

2.2. Естественные координатные оси. Вектор кривизны

Проведем в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную касательной, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоско­стям, образующую с этими плоскостями естественный трехгранник (рис. 2.10).

Рис. 2.10

Линия пересечения соприкасающейся и нормальной плоскостей на­зывается главной нормалью кривой.

Линия пересечения нормальной и спрямляющей плоскостей назы­вается бинормалью кривой.

Естественными координатными осями называются три взаимно перпендикулярные оси: касательная, направленная в сторону возраста­ния дуговой координаты, главная нормаль, направленная в сторону вогнутости кривой, и бинормаль, направленная по отношению к каса­тельной и главной нормали так же, как ось Оz направлена по отно­шению к осям Ох и Оу в правой системе координатных осей. Единичные векторы-орты этих осей обозначаются соответственно .

Естественные координатные оси имеют начало в точке М кривой и при движении точки М по этой кривой перемещаются вместе с ней, оставаясь взаимно перпендикулярными, но изменяя свое направление в пространстве.

Рис. 2.11

Вектор кривизны кривой в данной точке равен про­изводной от орта касательной к кривой по дуговой координате (рис. 2.11):

.

Так кик вектор кривизны расположен в соприкасающейся пло­скости и перпендикулярен орту , то он направлен по главной нор­мали к центру кривизны кривой (рис. 2.12).

Модуль вектора кривизны К определяется по формуле

Рис. 2.12

В дифференциальной геометрии доказывается, что предел отношения угла смежности ε к приращению дуговой координаты Δs при стремле­нии Δs к нулю равен кривизне кривой 1/ρ, где ρ - радиус кри­визны кривой в точке М.

2.3. Ускорение точки при задании ее движения естественным способом

Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормаль­ным ускорением, а другой направлен по касательной и называется касательным ускорением точки (рис. 2.13)

.

Касательное ускорение характеризует изменение скорости по модулю, а нормальное – изменение скорости по направлению.

Проекция ускорения точки на бинормаль равна ну­лю, так как вектор ускорения расположен в соприкасающейся плоскости.

Проекция ускорения на главную нормаль равна

,

т. е. проекция ускорения точки на главную нормаль равна квадрату модуля скорости точки, деленному на радиус кривизны траектории в соответствующей точке. Эта проекция всегда положительна. Из это­го следует, что нормальное ускорение точки всегда направлено к центру кривизны траектории и равно по модулю этой проекции.

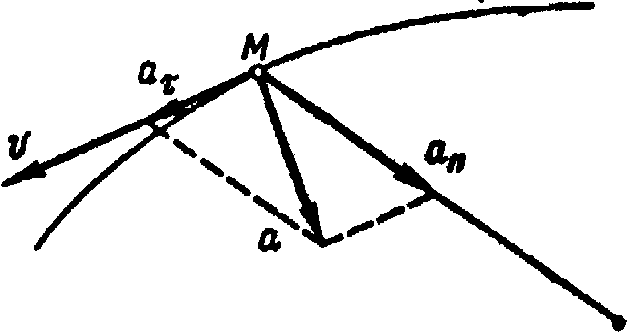
Рис. 2.13

Проекция ускорения на касательную равна

,

т.е. проекция ускорения точки на касательную равна второй произ­водной от дуговой координаты точки по времени или первой произ­водной от алгебраической величины скорости точки по времени.

Если известны траектория точки, ее радиус кри­визны ρ в любой точке и уравнение движения s=f(t), то можно найти проекции ускорения точки на естественные оси и по ним определить модуль и направление ускорения точки:

,

где - углы, образованные направлением ускорения с при­нятыми направлениями касательной и главной нормали в данной точке.