3.3. Угловая скорость и угловое ускорение тела

Величина, характеризующая быстро­ту изменения угла поворота φ с течением времени, называется угловой скоростью тела  и ее значение равно первой производной от угла поворота по времени

Принято правило знаков: если, глядя навстречу оси вращения, можно видеть поворот тела, происходящим против хода часовой стрелки, то угловая скорость считается положительной и наоборот, если < 0, то тело вращается по ходу часовой стрелки. Размерность угловой скорости

.

В технике угловую скорость часто измеряют числом оборотов в минуту, обозначая эту величину через об/мин. Так как за один оборот тело поворачивается на угол , а 1 мин = 60 с, то

.

Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела .

Если знаки и одинаковы, тело вращается ускоренно, а если их знаки различны - замедленно. Абсолютное значение углового ускорения

Размерность углового ускорения

.

Если dω/dt > 0, то угловая скорость ω увеличивается, т. е. тело вра­щается ускоренно. Если dω/dt < 0, то ω уменьшается, т. е. вращение про­исходит замедленно. Угловую скорость и угловое ускорение можно изобразить в виде векторов и , направленных вдоль оси вращения.

Когда тело вращается ускоренно, то величины и имеют одинаковые знаки и направление вектора совпадает с направлением вектора (рис. 2.27, а). Если тело вращается замедленно, то величины и имеют разные знаки и векторы и направлены вдоль оси вращения в противоположные стороны (рис. 2.27, б).

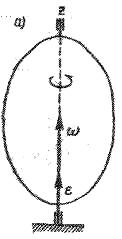
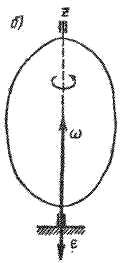
Рис. 2.27

Векторы и являются скользящими, так как точкой приложения их может быть любая точка оси вращения.

При вращении тела вокруг неподвижной оси все его точки имеют общие угловые параметры .

3.4. Равномерное вращение твердого тела

Вращение тела с постоянной угловой скоростью называется равномерным. Уравнение равномерного вращения твердого тела имеет вид

,

где - начальное значение угла поворота.

Из уравнения равномерного вращения тела при

,

т. е. угловая скорость равномерного вращения тела равна отношению приращения угла поворота за некоторый промежуток времени к этому промежутку времени.

3.5. Равнопеременное вращение твердого тела

Вращение тела, при кото­ром угловое ускорение постоянно, называют равнопеременным враще­нием. При этом, если абсолютная величина угловой скорости увеличи­вается, вращение называют равноускоренным, а если уменьшается - равнозамедленным.

Уравнение равнопеременного вращения тела имеет вид

,

где - начальное значение угла поворота; - начальная угловая скорость вращения; - угловое ускорение.

Угловая скорость в случае равнопеременного вращения твердого тела определяется по зависимости

.