но, чтобы равнодействующая равнялась нулю
.
Записанному условию равновесия в случае плоской системы сходящихся сил соответствуют два уравнения равновесия:
;
,
.
a) б)
в) г)
д) е)
з)
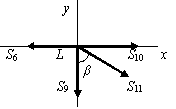
Рис. 1.75
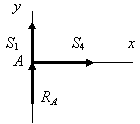
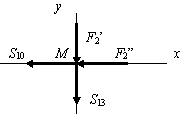
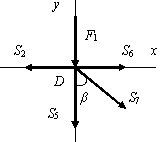
Узел М (рис. 1.75,б):
кН;
кН.
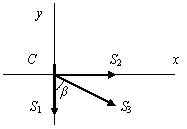
Узел С (рис. 1.75,в):
;
кН;
кН.
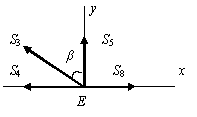
Узел Е (рис. 1.75,г):
кН;
кН.
Узел D (рис. 1.75,д):
кН;
кН.
Узел К (рис. 1.75,е):
кН;
кН.
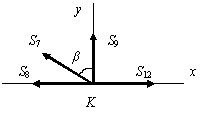
Узел L (рис. 1.75,ж):
кН.
Определение усилий в стержнях фермы методом сечений. Так же, как и при методе вырезания узлов, необходимо сначала определить реакции опор и проверить статическую определимость фермы. Определим усилия в стержнях методом сечений на примере уже рассмотренной фермы. Объектом равновесия является часть фермы, содержащая не менее двух узлов. Активные силы приложены к узлам фермы.
Если в задаче имеется распределенная нагрузка, то она должна быть
такой, чтобы равнодействующая, проходя через центр тяжести графика распределенной нагрузки, была приложена тоже к узлу фермы (рис. 1.76).
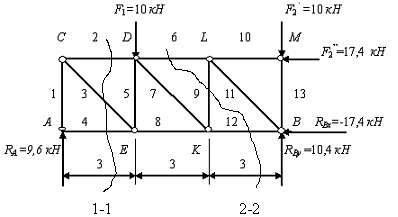
Рис. 1.76
Мысленно ферма рассекается на две части таким образом, чтобы сечение проходило не более чем через три стержня. Одна из частей отбрасывается и ее действие на оставшуюся часть фермы заменяется усилиями в рассеченных стержнях. Усилия направляются вдоль стержней из предположения, что все рассеченные стержни растянуты.
Для предупреждения лишних ошибок разумнее сохранить ориентацию координатных осей.
Сечение 1 -1. Изобразим левую отсеченную часть фермы, так как ее показ менее трудоемок (рис.1.77).
На отсеченную часть фермы действует плоская произвольная система сил, для которой условия равновесия записываются в виде:
.
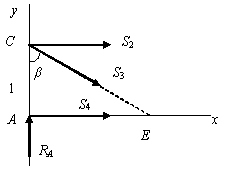
Рис. 1.77
Уравнения
равновесия должны быть такими, чтобы в
каждое входило не более одного неизвестного
усилия. В данном случае имеются
параллельные неизвестные усилия
,
поэтому необходимо использовать вторую
систему уравнений равновесия, содержащую
одно уравнение проекций и два уравнения
моментов, причем в качестве моментных
точек нужно взять точки пересечения
линий действия неизвестных усилий.
кН;
;
кН.
Сечение 2-2. Рассекать ферму на части можно не только вертикально, важно, чтобы при этом в сечение попадали только три стержня. При проведении сечения 2-2 менее трудоемким будет изображение правой отсеченной части (рис. 1.78).
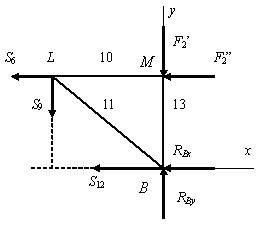
Рис. 1.78
Уравнения равновесия будут выглядеть следующим образом:
;
;
кН;
кН.
Глава 8. Рычаг. Сцепление и трение скольжения
8.1. Рычаг. Устойчивость при опрокидывании. Коэффициент устойчивости
Рычагом называется твердое тело, имеющее неподвижную ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной этой оси.
Положим,
что к рычагу в точках
приложены
задаваемые силы
,
лежащие в
плоскости чертежа, а ось рычага пересекает
эту плоскость в точке О,
которую называют опорной
точкой (рис.
1.79). Реакция
оси рычага, уравновешивая задаваемые
силы, лежит в их плоскости, но
направление ее не известно.
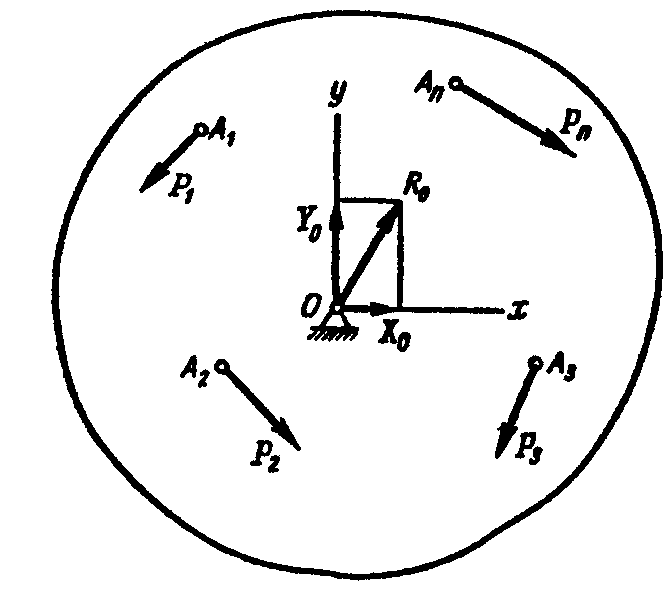
Рис. 1.79
Уравнение моментов задаваемых сил относительно опорной точки, не содержащее реакции оси рычага, выражает условие, которому удовлетворяют задаваемые силы, приложенные к рычагу, если он находится в покое.
Это условие формулируется так: если рычаг находится в покое, то алгебраическая сумма моментов всех задаваемых сил, приложенных к рычагу, относительно опорной точки равна нулю
.
Из этого условия, которое выполняется, если рычаг находится в покое, получим условие устойчивости тел при опрокидывании.
Пусть
к прямоугольному параллелепипеду (рис.
1.80) весом
на высоте d
приложена горизонтальная сила
,
которая может не только сдвинуть тело,
но и опрокинуть его при вращении вокруг
ребра А.
Считая, что
сила
недостаточно велика, чтобы сдвинуть
тело, рассмотрим ее опрокидывающее
действие. Обозначим а
расстояние
от точки А,
изображающей на чертеже ось вращения
рычага, до линии действия силы
,
которая препятствует опрокидыванию.
Составим сумму моментов задаваемых сил
и
относительно опорной точки А
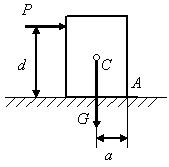
Рис. 1.80
,
откуда
.
Назовем абсолютные значения моментов сил и относительно точки А удерживающим и опрокидывающим моментами:
.
Тогда на границе устойчивости
.
При устойчивом состоянии тела
.
Устойчивость при опрокидывании в технике принято определять отношением числового значения удерживающего момента к числовому значению опрокидывающего момента:
.
Это отношение называют коэффициентом устойчивости. Очевидно, что в случае предельной устойчивости коэффициент устойчивости k = 1, а в случае устойчивого состояния k > 1.
Определить,
опрокинется ли тело под действием силы
или будет находиться в устойчивом
состоянии, можно и графическим путем.
Для этого продолжим линии действия сил
и
до их пересечения в точке К,
перенесем
силы в эту точку и найдем их равнодействующую
(рис. 1.81).
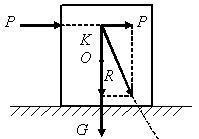
Рис. 1.81
Продолжая линию действия равнодействующей силы, найдем точку ее пересечения с опорной плоскостью. В рассмотренном примере возможны три случая.
1. Если эта точка лежит слева от ребра А, то состояние тела устойчиво.
2. Если линия действия равнодействующей пересекает ребро А, то состояние тела предельно устойчиво.
3. Если эта точка лежит справа от ребра А, то тело опрокинется.
8.2. Сцепление и трение скольжения
Если
к твердому телу, покоящемуся на шероховатой
горизонтальной плоскости (рис. 1.82),
приложить горизонтальную силу
,
то действие этой силы вызовет появление
силы сцепления
,
представляющей собой силу противодействия
плоскости смещению тела. Благодаря
сцеплению тело остается в покое при
изменении модуля силы
от нуля до некоторого значения
.
Это значит,
что модуль силы сцепления тоже изменяется
от
до
в момент начала движения.
Модуль
максимальной силы сцепления, как
показывает опыт, пропорционален
нормальному давлению
тела на плоскость. В рассматриваемом
случае N
= G.
Тогда
.
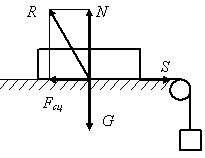
Рис. 1.82
Коэффициент
пропорциональности
является
отвлеченным числом и называется
коэффициентом
сцепления.
Коэффициент
сцепления зависит от материала и
физического состояния соприкасающихся
тел и определяется экспериментально.
Его величина для материалов,
используемых в технике, обычно меньше
единицы. Так как максимальное значение
силы сцепления равно
,
то модуль силы сцепления всегда
удовлетворяет условию
.
Направление силы сцепления противоположно направлению того движения, которое возникло бы под действием приложенных к телу сил при отсутствии сцепления.
При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Направление этой силы (рис. 1.83), противодействующей скольжению, противоположно направлению скорости тела.
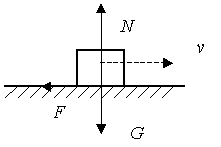
Рис. 1.83
Модуль силы трения скольжения пропорционален нормальному давлению N
.
Коэффициент пропорциональности f называется коэффициентом трения скольжения и определяется опытным путем.
Коэффициент трения скольжения является отвлеченной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления. Однако в элементарных расчетах зависимость коэффициента трения скольжения от скорости и удельного давления часто не учитывается. Экспериментально установлено, что
.
Реакция
реальной
(шероховатой) поверхности в отличие от
реакции идеальной (гладкой) поверхности
имеет две составляющие: нормальную
реакцию
и силу сцепления
(или силу трения
при движении тела). Угол
,
образованный реакцией шероховатой
поверхности с нормалью к поверхности
в предельном состоянии покоя при
,
называется углом
сцепления
(рис. 1.84).
Тангенс угла сцепления равен коэффициенту сцепления:
,
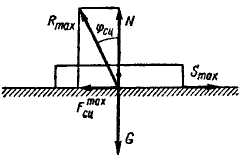
Рис. 1.84
или
.
Угол, тангенс которого равен коэффициенту трения скольжения, называется углом трения.
Задача 1.13. Вращающий момент электродвигателя лебедки равен М=1,2 кН∙м. Для остановки двигателя служат тормозные колодки тормоза А (рис. 1.85), прижимающиеся силами к тормозному диску В, жестко связанному с ротором двигателя. Радиус тормозного диска r= 600 мм. Определить силу давления , необходимую для удержания ротора в равновесии, если коэффициент трения между деревянными колодками и чугунным тормозным диском равен f = 0,5.
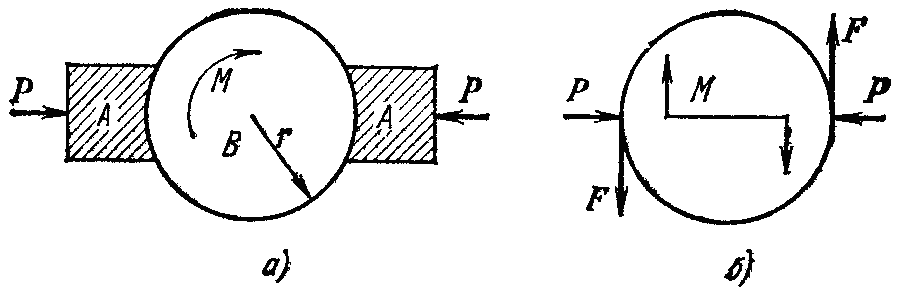
Рис. 1.85
Решение.
Рассмотрим равновесие тормозного диска
В
(рис. 1.85). К диску приложена задаваемая
пара — вращающий момент
.
Отбрасывая мысленно тормозные
колодки, заменяем их действие силами
реакций.
Каждая реакция раскладывается на две составляющие: нормальное давление и силу трения . Зависимость между нормальным давлением и силой трения выражается при помощи коэффициента трения
.
Для равновесия диска необходимо, чтобы сумма моментов всех сил, приложенных к диску, равнялась нулю. Силы взаимно уравновешиваются и в уравнение моментов не входят. Силы трения образуют пару сил; крутящий момент представляет собой также пару сил. Сумма моментов сил, составляющих пару относительно любой точки, равна моменту пары. Таким образом,
.
Подставляя значение силы трения в это уравнение, имеем:
,
откуда
кН.
Задача
1.14. Механическая
конструкция (рис. 1.86), состоящая из
груза весом Q
= 15
кH,
опоры
С,
барабана весом P
= 10
кH
и
тормозного устройства, находится
в покое, коэффициент сцепления
между
колодкой и барабаном
равен 0,1.
Определить значение силы и реакции опор
О,
А,
В,
приняв, что
=
300;
а
= 10
см;
b
= 20
см.
Рис. 1.86
Решение. Объектом равновесия является составная конструкция, состоящая из груза В, опоры С, барабана и тормозного устройства. Применим принцип освобождаемости от связей по всем связям системы (внешним и внутренним). При этом вместо конструкции получим три свободных тела (груз, барабан и тормозное устройство), находящихся в равновесии под действием системы сил. Опору С можно не принимать во внимание, так как активных сил к ней не приложено. Для каждого объекта равновесия необходимо составить расчетную схему в соответствии с известными правилами, собственно решение задачи начинаем с того объекта, к которому приложено меньшее количество неизвестных.
1.
Груз
В.
Размерами
груза В
в процессе движения можно пренебречь,
то есть считать его материальной точкой
(рис.
1.87).
Тогда объектом равновесия является
узел В,
активной силой -
сила тяжести
.
Применяя
принцип освобождаемости от связей,
мысленно отбросим связи (нить и идеальную
поверхность) и заменим их действие
реакциями
и
.
Направление оси х
принимаем по поверхности вниз, ось у
– перпендикулярно оси х
вверх.
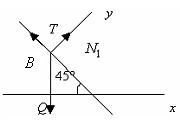
Рис. 1.87
Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая системы сил равнялась нулю.
.
Уравнения равновесия.
.
2.
Барабан.
Объектом равновесия является барабан.
Активная сила – сила тяжести
(рис. 1.88). Применяя принцип освобождаемости
от связей, мысленно отбросим связи (нить
и тормозное устройство) и заменим их
действие реакциями
,
.
Покажем силу сцепления
,
которая направлена по касательной к
барабану, в сторону, противоположную
возможному движению.
Для равновесия плоской произвольной системы сил необходимой достаточно, чтобы главный вектор этой системы сил и её главный момент относительно любого центра были равны нулю.
.
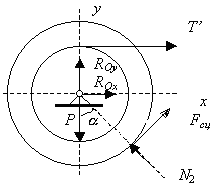
Рис. 1.88
Уравнения равновесия.
;
(а)
;
(б)
.
(в)
Сила сцепления между нормальной колодкой и барабаном определяется
.
Решая систему уравнений (а – в), получим:
;
;
.
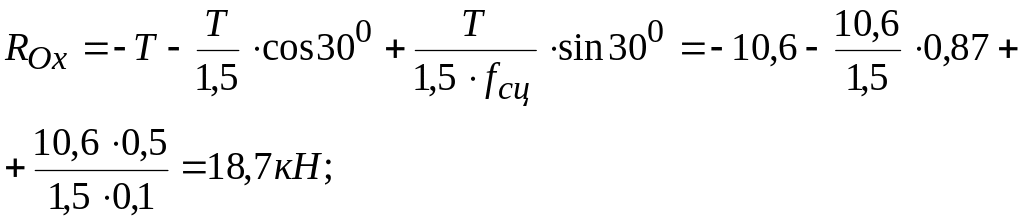
3.
Тормозное устройство.
Объект равновесия — шток
тормозного устройства. Активная сила
.
Используя
принцип освобождаемости
от связей, мысленно отбросим связи
(барабан и корпус
тормозного устройства) и заменим их
действие реакциями
(рис. 1.89).
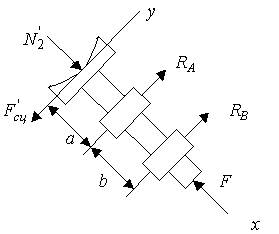
Рис. 1.89
Покажем
силу сцепления
,
равную по модулю
и направленную в
противоположную сторону. Направление
оси х
принимаем
по оси штока
вниз ось у
–
перпендикулярно
оси х
вправо.
Условия равновесия:
.
Уравнения равновесия:
;
(г)
;
(д)
.
(е)
Определение искомых величин, проверка правильности решения и анализ полученных результатов. Решая уравнения (г – е), получаем:
.
Подставляя числовые значения, получим:
.
.
Знак минус указывает на то, что реакция RB направлена в противоположную сторону.