§ 66. Передача отметок на монтажные горизонты

Высотным разбивочным обоснованием на каждом монтажном горизонте служат рабочие реперы, отметки которых получены от исходных реперов высотной разбивочной основы. На монтажный горизонт переносят не менее двух реперов в зависимости от числа секций. Рабочими реперами могут служить закладные детали в кон­струкциях данного этажа или откраски на строительных конст­рукциях.

Отметки на монтажный горизонт могут передаваться методом геометрического нивелирования с применением двух нивелиров и стальной компарированной рулетки. На исходном и монтажном горизонтах устанавливают нивелиры (рис. 92) (можно перено­сить один нивелир). На реперах, между которыми передаются от­метки, устанавливают рейки. Берут отсчеты а и b по рейкам и от­счеты ℓ₂ и ℓ₁ по подвешенной рулетке. Разность отсчетов ℓ = ℓ₂ – ℓ₁ необходимо исправить поправками за компарирование и темпера­туру. Искомую отметку монтажного горизонта Н_мон вычисляют по формуле

Н_мон = Н_исх + (а – b) + ℓ, (66.1)

где Н_исх – отметка репера на исходном горизонте.

Точность передачи отметки этим способом будет зависеть в ос­новном от ошибок отсчетов по рейкам и рулетке, компарирования реек и рулетки, учета температуры рулетки.

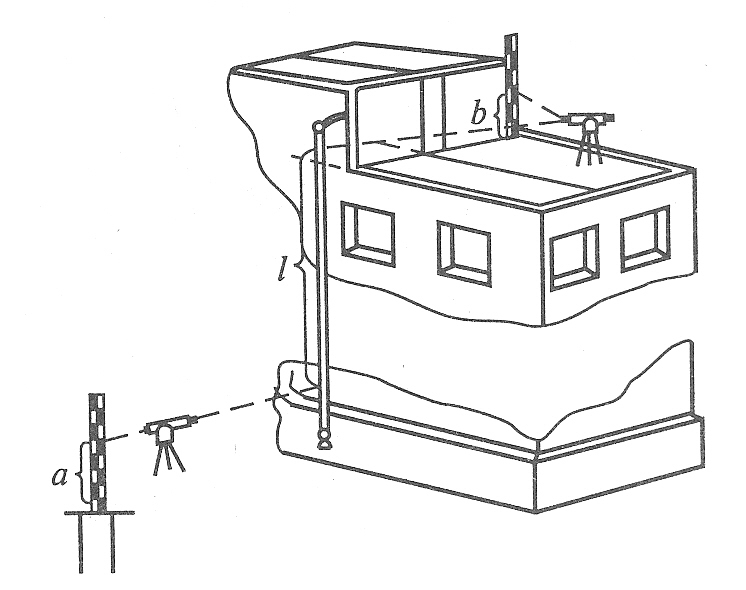
Рис. 92. Схема передачи отметки с исходного

на монтажный горизонт

Передача отметки на монтаж­ный горизонт может быть также выполнена путем фиксации от­метки на строительных конструк­циях исходного горизонта и вер­тикального линейного промера по строительным конструкциям до соответствующей откраски на монтажном горизонте.

Для удобства пользования стараются на монтажном горизонте зафиксировать отметку, кратную целым метрам или полуметрам, например: +24,000 или +24,500.

Для передачи отметки на дно котлована используется точно такой же способ как изложен выше. Следует только иметь ввиду, что отметка репера на дне котлована будет меньше чем отметка репера, расположенного на кромке котлована. Поэтому формулу (66.1) можно для этого случая переписать следующим образом:

Н_мон = Н_исх – (а – b) –ℓ . Назад

§ 67. Способы разбивки сооружений

Для выполнения разбивочных работ применяют следующие способы: полярных и прямоугольных координат, угловой, линейной и створной засечек.

Способ угловой засечки применяют для разбивки недоступных точек, находящихся на значительном расстоянии от исходных пунктов.

Различают прямую и обратную угловые засечки.

В способе прямой угловой засечки положение на местности проектной точки С (рис.93) находят отложением на исходных пунктах А и В проектных углов β₁ и β₂. Базисом засечки служит или специально измеренная сторона, или сторона разби­вочной сети. Проектные углы β₁ и β₂ вычисляют как разность ди­рекционных углов сторон. Дирекционные углы находят из решения обратной геодезической задачи по проектным координатам опре­деляемой точки и известным координатам исходных пунктов.

Н

Рис. 93. Схема разбивки способом прямой и линейной засечек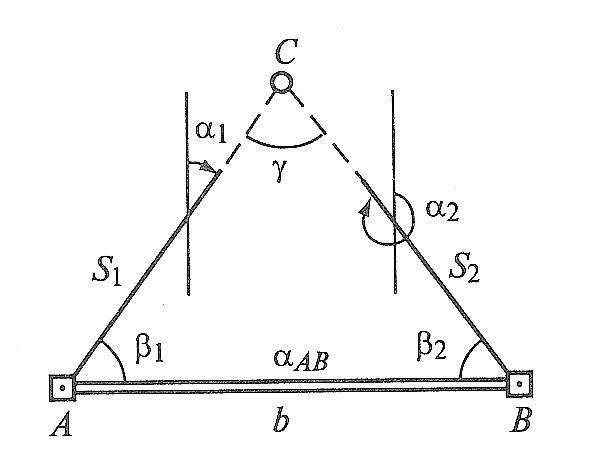

а точность разбивки способом прямой угловой засечки ока­зывают влияние погрешности: собственно прямой засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки. При разбивочных работах центрирование теодолита и визир­ных целей с помощью оптических отвесов, а также фиксация вы­носимой точки могут быть выполнены сравнительно точно. По­этому основными погрешностями, определяющими точность спо­соба прямой угловой засечки, являются погрешности собственно засечки и исходных данных. Суммарная величина этих погрешно­стей может составить значительных величин, что потребует выполнения угловой засечки с повышенной точностью.

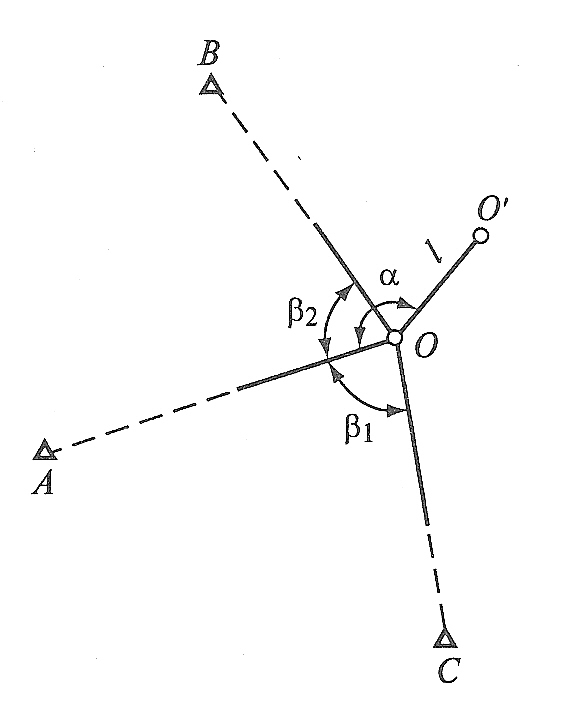
Т

Рис. 94. Схема способа обратной угловой засечки

ребуемая точность разбивки в этом случае может быть достигнута следу­ющим образом. Отложив с возможной точностью углы β_l И β₂, определяют в натуре положение точки С. Затем на опорных пунк­тах соответствующим числом приемов измеряют точное значение отложенных углов. Для приведенного примера при использовании теодолита 2Т30 надо выполнить не менее четырех приемов. Изме­ряют также угол γ на точке С. Распределив невязку в треугольнике поровну на все три угла, определяют координаты точки С. Срав­нивая их с проектными значениями, находят поправки (редук­ции), по которым в натуре смещают (редуцируют) приближенно вынесен­ную точку С. Такой способ называют способом замкнутого треугольника.

На принципе редуцирования основа­но и применение для разбивки спо­соба обратной угловой засеч­ки. На местности находят приближенно положение О' разбиваемой проектной точки О (рис. 94). В этой точке устанав­ливают теодолит и с требуемой точнос­тью измеряют углы не менее чем на три исходных пункта с известными коорди­натами. По формулам обратной засечки вычисляют координаты приближенно определенной точки и сравнивают их с проектными значениями. По разности координат вычисляют величины редукций (угловой и линейный элементы) и смещают точку в проектное положение.

Для контроля на этой точке измеряют углы, вновь вычисляют ее координаты и сравнивают их с проектными. В случае недопус­тимых расхождений все действия повторяют.

В способе линейной засечки положение выносимой в натуру точки С (см. рис. 93) определяют в пересечении проектных рас­стояний S₁и S₂, отложенных от исходных точек А и В. Этот способ обычно применяют для разбивки осей строительных конструкций в случае, когда проектные расстояния не превышают длины мерного прибора.

Наиболее удобно разбивку производить при помощи двух ру­леток. От точки А по рулетке откладывают расстояние S₁, а от точки В по второй рулетке – S₂. Перемещая обе рулетки при совмещенных нулях с центрами пунктов А и В, на пересечении кон­цов отрезков S₁и S₂ находят положение определяемой точки С.

­Способ полярных координат широко применяют при разбивке осей зданий, сооружений и конструкций с пунктов теодолитных или полигонометрических ходов, когда эти пункты расположены сравнительно недалеко от выносимых в натуру точек.

В этом способе положение определяемой точки С (рис. 95) находят на местности путем отложения от направления АВ проект­ного угла β и расстояния S. Проектный угол β находится как раз­ность дирекционных углов α_АВ и α_АС, вычисленных как и расстоя­ние S из решения обратных задач по координатам точек А, В и С. Для контроля положение зафиксированной точки С можно про­верить, измерив на пункте В угол β' и сравнив его со значением, полученным как разность дирекционных углов α_ВА и α_ВС'.

П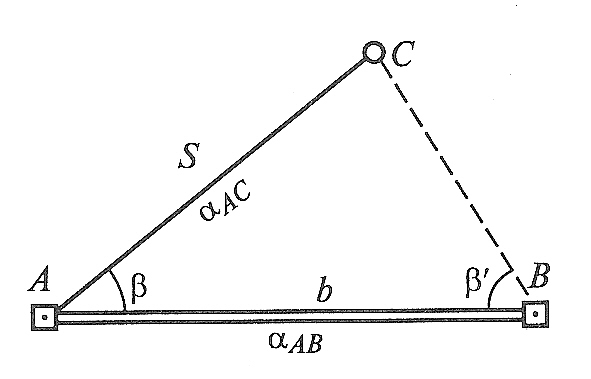 огрешность собственно разбивки полярным способом зави­сит от погрешности построения угла β и погрешности отло­жения проектного расстояния S. Расчет показывает, что для данных условий уменьшение по­грешности в положении выносимой в натуру точки возможно лишь при существенном уменьшении погрешности отложения проект­ного расстояния – хотя бы в два раза.

Е

Рис. 95. Схема разбивки способом полярных координат

сли разбиваемая точка находится на значительном расстоянии от исход­ного пункта, то приходится несколь­ко раз откладывать полярным спосо­бом проектные углы и расстояния, прокладывая проектный ход.

Способы створной и створно-линейной засечек широко при­меняют для выноса в натуру разбивочных осей зданий и сооруже­ний, а также монтажных осей конструкций и технологического оборудования.

Положение проектной точки С в способе створной за­сечки определяют на пересечении двух створов, задаваемых между исходными точками 1-1' и 2-2' (рис. 96). Створ задают обычно теодолитом, который центрируют над исходным пунктом (напри­мер, 1), а зрительную трубу ориентируют по визирной цели, отцен­трированной на другом исходном пункте (в данном случае 1'). Поло­жение точки С фиксируют в заданном створе.

Средняя квадратическая погрешность створной засечки зави­сит от погрешностей построения первого и второго ство­ров, а также погрешности фиксации опорных точек.

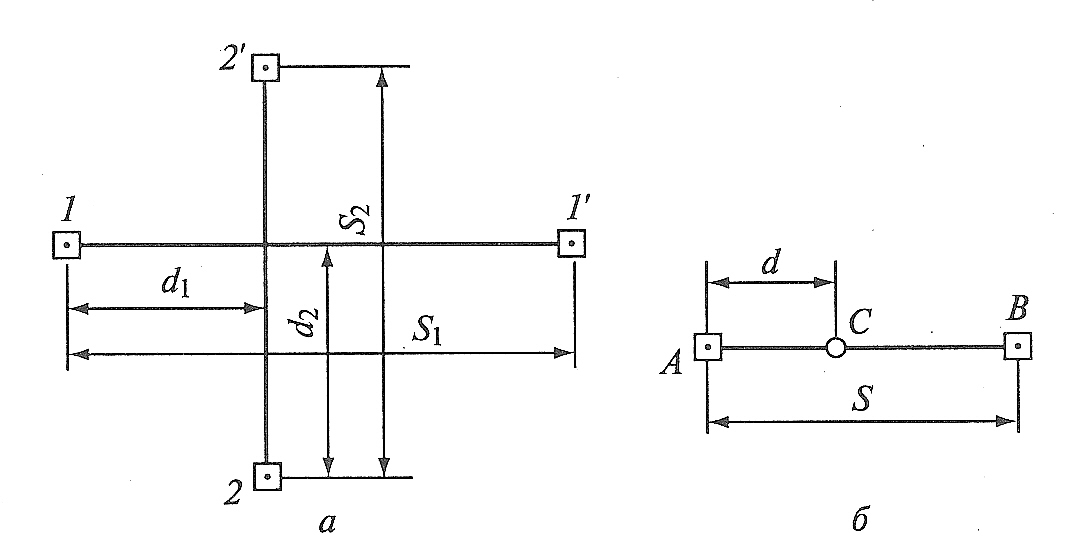
Рис. 96. Схема разбивки способами:

а – створной засечки; б – створно-линейной засечки

Створно-линейный способ позволяет определить про­ектное положение выносимой в натуру точки С (см. рис. 96) путем отложения проектного расстояния d по створу АВ.

Способ прямоугольных координат применяют в основном при наличии на площадке или в цехе промышленного предприятия строительной сетки, в системе координат которой задано поло­жение всех главных точек и осей проекта.

Р

Рис. 97. Схема разбивки способом прямоугольных координат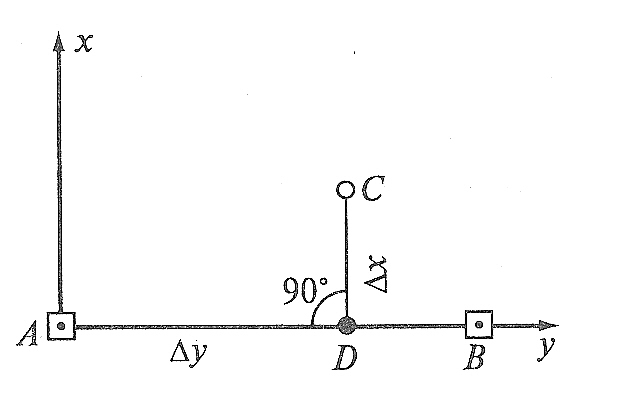

азбивку проектной точки С (рис. 97) производят по вычис­ленным значениям приращений ее координат ΔХ и ΔY от ближай­шего пункта сетки. Большее приращение (на рисунке ΔY) откла­дывают по створу пунктов сетки АВ. В полученной точке D уста­навливают теодолит и строят от стороны сетки прямой угол. По перпендикуляру откладывают меньшее приращение и закрепляют полученную точку С. Для контроля положение точки С можно оп­ределить от другого пункта строительной сетки. Схема способа прямоугольных координат, по существу, сочетает в себе схему створно-линейного и полярного способов.

Назад