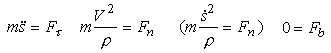- •Предмет и содержание динамики, основные понятия и определения. Законы Галилея-Ньютона.
- •Дифференциальные уравнения движения свободной и несвободной материальной точки в трех формах.
- •Две основные задачи динамики. Решение первой основной задачи динамики точки.
- •Основное уравнение относительного движения. Переносная и кориолисова силы инерции.
- •Принцип относительности классической механики. Инерциальные системы отсчета. Случай относительного покоя.
- •Свободные колебания материальной точки. Дифференциальное уравнение движения, его решение, частота и период свободных колебаний.
- •Влияние сил сопротивления, пропорциональных скорости точки, на свободные колебания (затухающие колебания). Декремент и логарифмический декремент колебаний.
- •Где − период свободных колебаний без сопротивления. Если , то сопротивление практически не влияет на период колебаний .
- •Вынужденные колебания при гармонической возмущающей силе без учета сил сопротивления. Амплитуда вынужденных колебаний. Коэффициент динамичности. Явление резонанса. Явление биений.
- •Механическая система, масса, центр масс и его координаты.
- •Осевые моменты инерции точки и системы. Радиус инерции. Моменты инерции простейших тел.
- •Теорема о моментах инерции относительно параллельных осей (теорема Гюйгенса - Штейнера).
- •Внешние и внутренние силы. Свойства внутренних сил.
- •Дифференциальные уравнения движения механической системы.
- •Теорема о движении центра масс. Следствия.
- •Количество движения материальной точки и механической системы. Элементарный и полный импульс силы.
- •Теорема об изменении количества движения точки и системы в дифференциальной и интегральной формах. Следствия.
- •Момент количества движения точки и системы относительно центра и оси. Кинетический момент вращающегося твердого тела.
- •Теорема об изменении кинетического момента точки и системы относительно центра и оси. Законы сохранения.
- •1. Если главный вектор всех внешних сил системы равен нулю ( ), то количество движения системы постоянно по величине и направлению.
- •2. Если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю ( ), то проекция количества движения системы на эту ось является постоянной величиной.
- •Элементарная и полная работа силы. Мощность силы.
- •Работа и мощность силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси.
- •Работа силы тяжести, силы упругости. Работа внутренних сил неизменяемой системы.
- •Кинетическая энергия точки и системы. Кинетическая энергия тела при поступательном, вращательном и плоскопараллельном движениях.
- •Теорема об изменении кинетической энергии точки и системы в трех формах.
- •Дифференциальные уравнения поступательного, вращательного и плоско - параллельного движений твердого тела.
- •Силовое поле. Потенциал силового поля. Силовая функция и потенциальная энергия. Эквипотенциальные поверхности. Закон сохранения механической энергии.
- •Связи, их уравнения и классификация.
- •Действительное и возможное перемещение. Возможная работа. Идеальные связи.
- •Принцип возможных перемещений.
- •Применение принципа возможных перемещений к определению реакций связей составных конструкций.
- •Сила инерции материальной точки. Главный вектор и главный момент сил инерции при различных случаях движения твердого тела.
- •5.2.1. Сила инерции материальной точки
- •5.2.2. Силы инерции в поступательном движении твердого тела
- •5.2.3. Силы инерции во вращательном движении твердого тела, имеющего плоскость материальной симметрии
- •Принцип Даламбера для точки системы. Метод кинетостатики.
- •Общее уравнение динамики.
- •Обобщенные координаты. Обобщенные силы и их вычисление. Случай потенциальных сил.
- •Уравнения равновесия и движения в обобщенных координатах.
- •Виды равновесия. Понятие об устойчивости равновесия.
- •Теорема Лагранжа-Дирихле.
- •Дифференциальные уравнения движения механической системы в обобщенных координатах или уравнения Лагранжа второго рода (без вывода).
- •Уравнения Лагранжа 2 рода для консервативных систем. Кинетический потенциал.
- •Этот результат получается проектированием предыдущего равенства на ось .
- •Удар точки о неподвижную поверхность. Коэффициент восстановления.
- •Для определения ударного импульса запишем теорему об изменении количества движения за время удара для одного из тел в проекции на направление движения . Откуда
- •При абсолютно упругом ударе ударный импульс в два раза больше, чем при абсолютно неупругом.
- •Прямой центральный удар двух тел. Теорема Карно.
Дифференциальные уравнения движения свободной и несвободной материальной точки в трех формах.
Для вывода уравнений воспользуемся второй и четвертой аксиомами динамики. Согласно второй аксиоме
ma = F |
(1) |
где, по четвертой аксиоме, F является равнодействующей всех сил, приложенных к точке.
С учетом последнего замечания выражение (1) часто называют основным уравнением динамики. По форме записи оно представляет собой второй закон Ньютона, где одна сила, согласно аксиоме независимости действия сил, заменена равнодействующей всех сил, приложенных к материальной точке.
Вспомнив, что a = dV / dt = d2r / dt = r'', получаем из (1) дифференциальное уравнение движения материальной точки в векторной форме:
mr'' = F |
(2) |
В общем случае сила F может быть функцией времени (t), положения (r) и скорости (r') материальной точки. К позиционным силам, зависящим от положения, относятся силы упругости, силы всемирного тяготения, а также силы притяжения или отталкивания тел, имеющих электрические или магнитные заряды. Силы, зависящие от скорости, встречаются при исследовании движения в сопротивляющейся вязкой среде (жидкой или газообразной). Очень редко в природе встречаются силы, зависящие от ускорения. Таким примером может быть электромагнитная сила притяжения в законе Вебера. Следовательно, в подавляющем большинстве случаев
F = F(t, r, r') |
(3) |
Отметим, что в технике различные силы часто создаются с помощью специальных устройств - амортизаторов, демпферов и т.д., а в системах автоматического управления с помощью датчиков, электронных устройств и исполнительных органов возможно создание сил, являющихся функциями любой производной по времени от перемещения.
Спроектируем (1) на оси инерциальной декартовой системы координат. Зная, что ax = x''; ay = y''; az = z'', получаем дифференциальные уравнения движения материальной точки в координатной форме или в проекциях на прямоугольные оси координат:
mx'' = Fx; my'' = Fy; mz'' = Fz |
(4) |
При координатном способе радиус-вектор точки является функцией координат точки r = r (x, y, z). Поэтому из выражения (3) следует, что
Fx = Fx(t, x, y, z, x', y', z'); Fy = Fy(t, x, y, z, x', y', z'); Fz = Fz(t, x, y, z, x', y', z'); |
(5) |
Спроектируем (1) на оси естественного трехгранника (касательную, главную нормаль и бинормаль). Ускорение лежит в соприкасающейся плоскости и поэтому на бинормаль не проектируется, т.е. ab = 0. Учитывая, что aτ = s'', а an = V2 / ρ = s'2 / ρ, получаем дифференциальные уравнения движения материальной точки в естественной форме или в проекциях на оси естественного трехгранника:
|
(6) |
Напомним, что при естественном способе задания положение точки определяется дуговой координатой s, и поэтому
Fτ = Fτ(t, s, s'); Fn = Fn(t, s, s'); |
(7) |
Дифференциальные уравнения можно составить и в любых других системах координат (полярной, сферической и т.д.), проектируя на эти оси (1), зная как выражаются проекции ускорения в данных осях координат.
Дифференциальные уравнения движения несвободной материальной точки.
Согласно аксиоме связей, заменив связи их реакциями, можно рассматривать несвободную материальную точку, как свободную, находящуюся под действием активных сил и реакций связей. Тогда в выражении (1), согласно четвертой аксиоме динамики, F будет равнодействующей активных сил и реакций связей.
Поэтому дифференциальные уравнения движения свободной материальной точки можно использовать для описания движения несвободной точки, помня о том, что проекции сил на прямоугольные оси Fx, Fy, Fz в уравнениях (4) и проекции сил на естественные оси Fτ, Fn, Fb в уравнениях (6) включают в себя не только проекции активных сил, но и проекции реакций связей.