Переходные вероятности. Матрица перехода.

Переходной вероятностью называют условную вероятность того, что из состояния в итоге следующего испытания система перейдет в состояние . Таким образом, индекс относится к предшествующему, а - к последующему состоянию.

Будем считать, что число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

,

где представляют вероятности перехода за один шаг.

Отметим некоторые особенности матрицы перехода.

• Элементы каждой строки матрицы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и вероятность отсутствия перехода (элемент строки с равными индексами)

• Элементы столбцов задают вероятности всех переходов системы за один шаг в заданное состояние

• Так как в каждой строке матрицы помещены вероятности событий (т.е. вероятности перехода из состояния в любое возможное состояние ), которые образуют полную группу, то сумма вероятностей этих событий равна единице:

• По главной диагонали матрицы перехода стоят вероятности 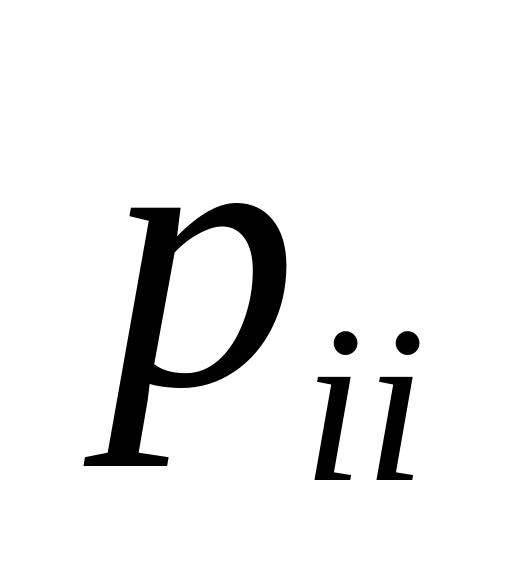того, что система не выйдет из состояния, а останется в нем.

Равенство Маркова

Обозначим через вероятность того, что в результате n шагов (испытаний) система перейдет из состояния в состояние . Например, - вероятность перехода за 10 шагов из третьего состояния в шестое. Отметим, что при n = 1 эта вероятность сводится просто к переходной вероятности .

Возникает вопрос, как, зная переходные вероятности , найти вероятности перехода состояния в состояние за n шагов. С этой целью вводится в рассмотрение промежуточное (между и ) состояние r. Другими словами, полагают, что из первоначального состояния за m шагов система перейдет в промежуточное состояние r с вероятностью , после чего за оставшиеся n – m шагов из промежуточного состояния r она перейдет в конечное состояние с вероятностью . Используя формулу полной вероятности, можно показать, что справедлива формула

Эту формулу называют равенством Маркова.

Зная все переходные вероятности , т.е. зная матрицу перехода из состояния в состояние за один шаг, можно найти вероятности перехода из состояние в состояние за два шага, а значит, и саму матрицу перехода , далее – по известной матрице - найти и т.д.

Действительно, полагая в равенстве Маркова n = 2, m = 1 получим

или . В матричном виде это можно записать как .

Полагая n=3, m =2, получим . В общем случае справедливо соотношение

.

Пример. Пусть матрица перехода равна

Требуется найти матрицу перехода

.

Умножая матрицу саму на себя, получим

.

Для практических применений чрезвычайно важным является вопрос о расчете вероятности нахождения системы в том или ином состоянии в конкретный момент времени. Решение этого вопроса требует знания начальных условий, т.е. вероятностей нахождения системы в определенных состояниях в начальный момент времени. Начальным распределением вероятностей марковской цепи называется распределение вероятностей состояний в начале процесса

.

Здесь через обозначена вероятность нахождения системы в состоянии в начальный момент времени. В частном случае, если начальное состояние системы в точности известно (например ), то начальная вероятность , а все остальные равны нулю.

Если для однородной цепи Маркова заданы начальное распределение вероятностей и матрица перехода, то вероятности состояний системы на n-м шаге вычисляются по рекуррентной формуле

.

Для иллюстрации приведем простой пример. Рассмотрим процесс функционирования некоторой системы (например, прибора). Пусть прибор в течение одних суток может находиться в одном из двух состояний – исправном ( ) и неисправном ( ). В результате массовых наблюдений за работой прибора составлена следующая матрица перехода

,

где - вероятность того, что прибор останется в исправном состоянии;

- вероятность перехода прибора из исправного в неисправное состояние;

- вероятность перехода прибора из неисправного в исправное состояние;

- вероятность того, что прибор останется в состоянии "неисправен".

Пусть вектор начальных вероятностей состояний прибора задан соотношением

, т.е. (в начальный момент прибор был неисправен). Требуется определить вероятности состояния прибора через трое суток.

Решение: Используя матрицу перехода, определим вероятности состояний после первого шага (после первых суток):

.

Вероятности состояний после второго шага (вторых суток) равны

Наконец, вероятности состояний после третьего шага (третьих суток) равны

.

Таким образом, вероятность того, что прибор будет находиться в исправном состоянии равна 0,819, и того, что в неисправном – соответственно 0,181.