9. Понятие слау. Осн. Опред-я. Матричная запись слау.

Системой m линейных уравнений с n неизвестными называется система вида

где и (i=1,…,m; b=1,…,n) — некоторые известные числа, а — неизвестные. Опред.: СЛАУ назыв. однородной, если все её свободные члены = 0 и неоднородной, если хотябы один св. член ≠ 0.

Опред.: Линейное ур-ие назыв. квадратным, если число m совпадает с числом неизвестных n.

Опред.: Решением СЛАУ назыв. такая совокупность n-чисел с1, с2, … , cn, которая при подстановки в систему на место неизвестных x1, x2, … , xn обращает все ур-ия этой системы в тождества.

Опред.: СЛАУ назыв. совместной, если она имеет хотябы одно решение, и несовместной, если решений нет.

Опред.: СЛАУ назыв. определённой, если она имеет единстенное решение и неопределённой, если решений >1.

Матричная запись – A*X=B

10. Совместность слау. Теорема Кронекера-Капелли.

Опред.: СЛАУ назыв. совместной, если она имеет хотябы одно решение, и несовместной, если решений нет.

Теорема: СЛАУ совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных. rg A=rg

Док-во: 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А → А^* не изменяют ранга.

            2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

11. Формулы Крамера. Решение системы с использованием обратной матрицы.

Метод Крамера состоит в том, что мы последовательно находим главный опред-ль системы , т.е. опред-ль матрицы А. ∆ = det (a_{i j}) и n вспомогательных опред-ей ∆ _i (i= ), которые получаются из опред-ля ∆ заменой i-го столбца столбцом свободных членов. Формулы Крамера имеют вид: ∆ * x _i = ∆ i  ( i  =  ). Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный опред-ль системы отличен от 0, то система имеет единственное решение, определяемое по формулам: x _i = ∆ i / ∆. Если главный опред-ль системы ∆ и все вспомогательные опред-ли ∆ i = 0 (i=  ), то система имеет бесчисленное множество решений. Если главный опред-ль системы ∆ = 0, а хотя бы один вспомогательный опред-ль отличен от 0, то система несовместна.

Пример: Решить методом Крамера систему уравнений:

                                               x₁ +   x₂ +  x₃ +      x₄ = 5,

                                               x₁ + 2x₂ -   x₃ +    4x₄ = -2,

                                             2x₁ -  3x₂ -   x₃ -     5x₄ = -2,

                                             3x₁ +   x₂ +2x₃ + 11 x₄ = 0.

Решение. Главный определитель этой системы

∆ = = -142 ≠ 0 

значит, система имеет единственное решение. 

12. Структура общего решения совместной неоднородной слау.

Теорема. Если ранг r матрицы неоднородной СЛАУ меньше числа неизвестных n, то общее решение системы можно записать в виде

, где — произвольные константы, а — фундаментальная система решений однородной системы, — некоторое известное (частное) решение неоднородной системы.

Док-во: Вспомним одно из свойств решений линейной неоднородной системы:

Если и — два решения системы , то вектор — решение приведенной однородной системы .

Поскольку выражение 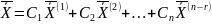, задает все решения однородной системы, то для любых двух решений и неоднородной системы справедливо и, следовательно, выражение определяет любое решение неоднородной системы.

Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.