Преобразование матрицы линейного оператора при переходе к новому базису.
Пусть V –
линейное пространство, А –
линейный оператор из 
, 
и 
–
два базиса в V и 
–
формулы перехода от базиса 
к
базису 
.
Обозначим через 
матрицу
перехода от базиса к базису. Отметим,
что ранг матрицыС равен n.
Пусть
и 
–
матрицы оператора А в
указанных базисах.
Теорема
7.1. Матрицы А и 
оператора А в
базисах
и
связаны
соотношением 
.
Доказательство. При
воздействии линейного
оператора А вектор 
пространства 
переводится
в вектор 
этого
пространства, т.е. справедливо равенство
= А (7.3)
(в старом базисе) и равенство
= А
(7.4)
(в
новом базисе). Так как 
–
матрица перехода от старого базиса к
новому, то
(7.5)
(7.6)
Умножим
равенство (7.5) слева на матрицу 
,
получим А
= АC
и
с учетом (7.3)
= АC
.
Заменив левую часть полученного выражения
в соответствии с (7.6),
получим: С
= АC
или
= С–1 АC
.
Сравнивая найденное выражение с
равенством (7.4), получим доказываемую
формулу.
Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса.
46. Понятие невырожденного оператора, его свойства.
Для
всякого линейного оператора А
А
.
При этом если А
только
при
,
то оператор называетсяневырожденным;
если же найдется такой вектор 
,
что А
,
то оператор А – вырожденный.
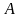х=0
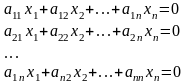
Это
однородная система обладает решением
отличным от нулевого, т.е.
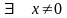
когда
определитель матрицы этой системы равен
0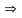
для
того чтобы ЛО был невырожденным необх.
и дост., чтобы det
A
.
Для
любого невырожд. ЛО
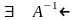верно
и обратное.
Утв. Невырожденный ЛО переводит ЛН векторы в ЛН векторы.
Пусть
-невырожд.ЛО,
пусть есть некоторое количество ЛН
векторов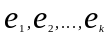
Покажем,
что
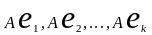—ЛН
(٭)
,
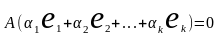т. к.
невырожд.
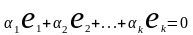и
векторы
ЛН
равенство
(٭)
выполняется когда
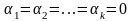—ЛН.
След.Если
подпространство
r-мерно
и
невырожд.ЛО,
то
—
r-мерно.
47. Характеристический многочлен, характеристическое уравнение.
Пусть А - линейный оператор(ЛО), Е - тождественный вектор.
Опр. Многочлен относительно λ: det(A- Eλ) называется характеристическим многочленом оператора А.
Пусть е1,..en- какой-либо базис А и пусть А=(аik) – матрица ЛО А в базисе, поэтому det A=detА, тогда
.
Обозначим через αk коэффициенты характеристич-го многочлена, стоящие при различных степенях х в ст. к => det(A-Eλ)=сумме αk*λ(в степени)к, где k от 0 до n.
Так как определитель оператора не зависит от выбора базиса, =>от выбора базиса не зависят и коэффициенты αk. Т.о. коэффициенты характерного многочлена являются инвариантами (величинами, не зависящими от выбора базиса).
Опр. Уравнение det(A-Eλ)=0 называется характеристическим уравнинием оператора А.
Опр. Число λ является собственным значением (СЗ) оператора А, если существует ненулевой вектор х, принадлежащий R, т.ч. х – собственный вектор оператора А.
48. Собственные значения и собственные векторы линейного оператора. Спектр оператора. Существование собственных значений оператора.
49. Диагонализуемость матрицы линейного оператора.
Т. Для того, чтобы матрица А ЛО А в базисе е1,..en была диагональной, необходимо и достаточно, чтобы базисные векторы еk, где k от 1 до n, являлись СВ этого оператора.
Д-во. 1) Пусть е1,..en –СВ А => Аek=λkek k от 1 до n, =>
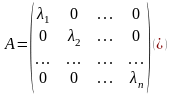
2) Пусть в базисе е1,..en матрицы А ЛО имеет диагональный вид (*) => Аek=a1ke1+a2ke2+…+anken, где k от 1 до n. Из вида диагональной матрицы следует, что это равенство сходится к Аek=λkek k от 1 до n,=> еk, где k от 1 до n, –СВ А.
Т. Пусть СЗ λ1… λp оператора А различны, тогда соответствующие им собственные векторы е1… еp ЛН (линейно независимы).
Д-во. Т.к. е1≠0 => он ЛН. Предположим, что теорема выполняется для векторов е1… еm. Докажем, что теорема справедлива и для векторов е1… еm, em+1. Т.е. покажем, что эти векторы ЛН.
α1е1+…+αmеm + αm+1еm+1=0.(1) Подействуем на обе части (1) оператором А:
α1Ае1+…+ αmАеm + αm+1Аеm+1 =0. По определению собственных векторов
α1λ1е1+…+ αmλmеm + αm+1λm+1еm+1 =0. (2) . Умножим обе части (1) на λm+1:
α1 λm+1е1+…+ αm λm+1еm + αm+1λm+1еm+1 =0.(3).
Вычтем из (2) (3):
α1(λ1- λm+1)е1+…+ αm(λm- λm+1)еm=0.<=> α1=…= αm=0.
≠0
≠0
ЛН по предположению индукции.
Возвращаемся к равенству (1): αm+1еm+1=0 <=> αm+1=0, т.к еm+1≠0 как собственный вектор. Т.о. все коэффициенты α1=…=αm = αm+1=0 => из (1) следует, что e1, e2,…,em, em+1 – ЛН
Следствие если характеристический многочлен оператора А имеет n различных корней, то в нек. базисе матр. этого ЛО имеет диагональный вид.
Опр. Совокупность всех собств. значений ЛО называется спектром этого оператора
50. Линейная независимость собственных векторов, соответствующих различным собственным значениям.