
- •Понятие матрицы. Осн. Операции над матрицами. Сложение матриц и умножение матрицы на число. Св-ва этих операций.
- •Понятие матрицы. Осн. Операции над матрицами. Умножение матриц и транспонирование матриц. Св-ва этих операций.
- •Определители 2-ого и 3-его порядков. Понятие определителя n-порядка.
- •Миноры и алгебраические дополнения эл-тов матрицы. Способы вычисления определителей.
- •Обратная матрица.
- •Ранг матрицы. Способы вычисления. Теорема о ранге матрицы. Метод окаймляющих миноров.
- •8. Ранг матрицы. Способы вычисления. Метод элементарных преобразований.
- •9. Понятие слау. Осн. Опред-я. Матричная запись слау.
- •10. Совместность слау. Теорема Кронекера-Капелли.
- •11. Формулы Крамера. Решение системы с использованием обратной матрицы.
- •12. Структура общего решения совместной неоднородной слау.
- •13. Однородные слау. Св-ва решений. Фундаментальная система решений однородной слау.
- •14. Метод последовательных исключений Гаусса решения слау.
- •15. Декартовы прямоугольные системы координат. Полярные системы координат.
- •16. Простейшие задачи аналитической геометрии.
- •17. Понятие вектора. Линейные операции над в-ми и их св-ва.
- •18. Коллинеарность в-ов. Геом. Смысл линейной зависимости двух в-ов.
- •19. Компланарность. Геом. Смысл линейной зависимости 3-ёх в-ов.
- •20 Линейная зависимость четырех векторов.
- •21. Базис и координаты в-ов на пл-ти и в пространстве. Декартовы прямоугольные координаты, основные формулы. Геом. Смысл декартовых прямоугольных координат вектора.
- •Базис в декартовой прямоугольной системе координат. Геометрический смысл декартовых прямоугольных координат вектора.
- •22. Скалярное произведение в-ов. Опред., осн. Св-ва. Выражение скалярного произведения через координаты сомножителей.
- •23. Векторное произведение. Опред., геом. Смысл, осн. Св-ва. Выражение векторного произведения через координаты сомножителей.
- •24. Смешанное произв. В-ов, его геом. Смысл и осн. Св-ва. Выражение смешанного произведения в-ов через координаты сомножителей.
- •25. Общее ур-ие прямой на плоскости и его исследование. Ур-ие прямой в отрезках.
- •Уравнение прямой в пространстве, проходящей через 2 заданные точки.
- •26. Каноническое ур-ие прямой на плоскости. Ур-ие прямой, проходящей через две заданные точки. Параметрические ур-ия прямой. Ур-ие прямой с угловым коэффициентом.
- •27. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
- •28. Нормированное ур-ие прямой на пл-ти. Приведение общего ур-ия прямой на пл-ти к нормированному виду. Расстояние от точки до прямой на пл-ти.
- •30. Угол между 2-мя пл-ми. Условия || и двух плоскостей. Ур-ие пл-ти, проходящей через три заданные точки.
- •31. Нормированное ур-ие пл-ти. Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
- •32. Прямая в пространстве как линия пересечения двух пл-тей. Канонические и параметрические ур-ия. Ур-ия прямой, проходящей через две заданные точки.
- •33. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Исследование взаимного расположения двух прямых в пространстве.
- •Преобразование матрицы линейного оператора при переходе к новому базису.
30. Угол между 2-мя пл-ми. Условия || и двух плоскостей. Ур-ие пл-ти, проходящей через три заданные точки.
Угол между 2-мя плоскостями. Условие паралл-ти и перп-ти 2-х плоскостей.
Пусть
две плоскости π1
и
π2
заданы
общими уравнениями A1x+B1y+C1z+D1=0
и A2x+B2y+C2z+D2=0.
Так как нормальным вектором плоскости
π1
является вектор
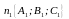 ,
а нормальным вектором плоскости π2
является
вектор
,
а нормальным вектором плоскости π2
является
вектор
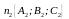 ,
то задача об определении угла между π1
и
π2.
Из
определения скалярного произведения
,
то задача об определении угла между π1
и
π2.
Из
определения скалярного произведения
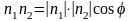 ,
и из выражения в координатных длин
векторов n1
и n2,
и
их скалярного произведения, получим
,
и из выражения в координатных длин
векторов n1
и n2,
и
их скалярного произведения, получим
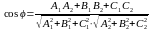 (1).
Таким образом, угол φ между плоскостями
π1
и
π2
определяется по этой формуле.
(1).
Таким образом, угол φ между плоскостями
π1
и
π2
определяется по этой формуле.
Условия перпендикулярности плоскостей π1 и π2 вытекает из формулы (1) (при cosφ=0), т.е. A1A2+B1B2+C1C2=0
Условие
параллельности плоскостей π1
и
π2,
эквивалентное условию коллинеарности
векторов n1
и n2
, заключается в пропорциональности
координат этих векторов, т.е.

Ур-е пл-ти , проходящей через 3 заданные.
П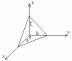 усть
даны три различные точки
усть
даны три различные точки
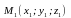 ,
,
 и
и
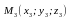 ,
не лежащие на одной прямой. Так как
указанные точки не лежат на одной прямой,
векторы
,
не лежащие на одной прямой. Так как
указанные точки не лежат на одной прямой,
векторы
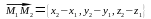 и
и
 не коллинеарные, следовательно, точка
не коллинеарные, следовательно, точка
 лежит в одной плоскости с точками M1,
M2
и M3
тогда
и только тогда, когда векторы
лежит в одной плоскости с точками M1,
M2
и M3
тогда
и только тогда, когда векторы
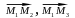 и
и
 компланарны, т.е. тогда и только тогда,
когда смешанное произведение этих трёх
векторов равно нулю. Используя выражение
смешанного произведения в координатах,
получим уравнение первой степени искомой
плоскости, проходящей через три заданные
точки:
компланарны, т.е. тогда и только тогда,
когда смешанное произведение этих трёх
векторов равно нулю. Используя выражение
смешанного произведения в координатах,
получим уравнение первой степени искомой
плоскости, проходящей через три заданные
точки:

31. Нормированное ур-ие пл-ти. Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
Нормированное уравнение плоскости.
Рассм.
любую пл-ть π. Проведём через начало
координат О прямую n,
перпендикулярную пл-ти π, и обозначим
буквой p
точку пересечения прямой n
пл-ти π. На прямой n
возьмём единичный вектор n,
наплавление
которого совпадает с направлением
отрезка
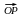 (в случае совпадения О и Р направление
берём произвольно). В
(в случае совпадения О и Р направление
берём произвольно). В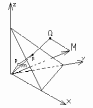 ыразим
уравнение плоскости π через: 1) длину р
отрезка
,
2) углы α, β и γ наклона вектора n
к осям Ox,
Oy
и Oz
соответственно. Так как n
– единичный
вектор, то его координаты, соответственно
равные его проекциям на оси координат,
имеют вид
ыразим
уравнение плоскости π через: 1) длину р
отрезка
,
2) углы α, β и γ наклона вектора n
к осям Ox,
Oy
и Oz
соответственно. Так как n
– единичный
вектор, то его координаты, соответственно
равные его проекциям на оси координат,
имеют вид
 (1).
Точка M(x,y,z)
лежит на рассматриваемой плоскости π
тогда и только тогда, когда проекция
вектора
(1).
Точка M(x,y,z)
лежит на рассматриваемой плоскости π
тогда и только тогда, когда проекция
вектора
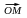 на ось, определяемую вектором n,
равна
р,
т.е. при условии прnOM=p.
В силу определения скалярного произведения
прnOM=n•OM.
Так как
на ось, определяемую вектором n,
равна
р,
т.е. при условии прnOM=p.
В силу определения скалярного произведения
прnOM=n•OM.
Так как
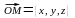 ,
а вектор n
определяется равенством (1), получим
,
а вектор n
определяется равенством (1), получим
 .
Следовательно точка M(x,y,z)
лежит на плоскости π тогда и только
тогда, когда координаты этой точки
удовлетворяют уравнению xcosα+ycosβ+zcosγ-p=0,
которое называется нормированным
уравнением плоскости.
.
Следовательно точка M(x,y,z)
лежит на плоскости π тогда и только
тогда, когда координаты этой точки
удовлетворяют уравнению xcosα+ycosβ+zcosγ-p=0,
которое называется нормированным
уравнением плоскости.
Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
Для
приведения общего уравнения плоскости
Ax+By+Cz+D=0
к нормированному виду следует умножить
его на нормирующий множитель
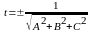 ,
знак противоположен знаку D.
,
знак противоположен знаку D.
Док. Т.к. общее уравнение должны определять одну и ту же плоскость, то в силу замечания, доказанного найдется число t: tA = cosα, tB = cosβ, tC = cosγ, tD = –p (1).
Возводя
в квадрат первые три равенства, складывая
их и учитывая, что сумма квадратов
направляющих косинусов равна 1, получим
t2(A2+C2+B2)=1,
откуда
 .
.
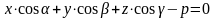 - нормированное уравнение плоскости.
- нормированное уравнение плоскости.
Т.к по смыслу расстояние p, то из четвертого уравнения (1) следует, что знак t противоположен знаку D.
Отклонением
т.М от П наз-ся число
 ,
если М и О лежат по разные стороны от
пл-ти, и –d
если по одну.
,
если М и О лежат по разные стороны от
пл-ти, и –d
если по одну.
Теорема:
Левая
часть нормированного уравнения плоскости
=
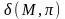 отклонению т.М(x,y,z)
от этой плоскости.
отклонению т.М(x,y,z)
от этой плоскости.
Док_во: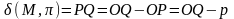 ,
,
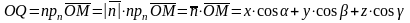 ,
,
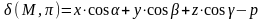 .
Для того чтобы найти
(Mo(Xo,Yo,Zo))
следует в левую часть нормир. ур-я пл-ти
вместо x,y,z
подставить Xo,Yo,Zo
– точки Mo.
.
Для того чтобы найти
(Mo(Xo,Yo,Zo))
следует в левую часть нормир. ур-я пл-ти
вместо x,y,z
подставить Xo,Yo,Zo
– точки Mo.
