
- •Понятие матрицы. Осн. Операции над матрицами. Сложение матриц и умножение матрицы на число. Св-ва этих операций.
- •Понятие матрицы. Осн. Операции над матрицами. Умножение матриц и транспонирование матриц. Св-ва этих операций.
- •Определители 2-ого и 3-его порядков. Понятие определителя n-порядка.
- •Миноры и алгебраические дополнения эл-тов матрицы. Способы вычисления определителей.
- •Обратная матрица.
- •Ранг матрицы. Способы вычисления. Теорема о ранге матрицы. Метод окаймляющих миноров.
- •8. Ранг матрицы. Способы вычисления. Метод элементарных преобразований.
- •9. Понятие слау. Осн. Опред-я. Матричная запись слау.
- •10. Совместность слау. Теорема Кронекера-Капелли.
- •11. Формулы Крамера. Решение системы с использованием обратной матрицы.
- •12. Структура общего решения совместной неоднородной слау.
- •13. Однородные слау. Св-ва решений. Фундаментальная система решений однородной слау.
- •14. Метод последовательных исключений Гаусса решения слау.
- •15. Декартовы прямоугольные системы координат. Полярные системы координат.
- •16. Простейшие задачи аналитической геометрии.
- •17. Понятие вектора. Линейные операции над в-ми и их св-ва.
- •18. Коллинеарность в-ов. Геом. Смысл линейной зависимости двух в-ов.
- •19. Компланарность. Геом. Смысл линейной зависимости 3-ёх в-ов.
- •20 Линейная зависимость четырех векторов.
- •21. Базис и координаты в-ов на пл-ти и в пространстве. Декартовы прямоугольные координаты, основные формулы. Геом. Смысл декартовых прямоугольных координат вектора.
- •Базис в декартовой прямоугольной системе координат. Геометрический смысл декартовых прямоугольных координат вектора.
- •22. Скалярное произведение в-ов. Опред., осн. Св-ва. Выражение скалярного произведения через координаты сомножителей.
- •23. Векторное произведение. Опред., геом. Смысл, осн. Св-ва. Выражение векторного произведения через координаты сомножителей.
- •24. Смешанное произв. В-ов, его геом. Смысл и осн. Св-ва. Выражение смешанного произведения в-ов через координаты сомножителей.
- •25. Общее ур-ие прямой на плоскости и его исследование. Ур-ие прямой в отрезках.
- •Уравнение прямой в пространстве, проходящей через 2 заданные точки.
- •26. Каноническое ур-ие прямой на плоскости. Ур-ие прямой, проходящей через две заданные точки. Параметрические ур-ия прямой. Ур-ие прямой с угловым коэффициентом.
- •27. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
- •28. Нормированное ур-ие прямой на пл-ти. Приведение общего ур-ия прямой на пл-ти к нормированному виду. Расстояние от точки до прямой на пл-ти.
- •30. Угол между 2-мя пл-ми. Условия || и двух плоскостей. Ур-ие пл-ти, проходящей через три заданные точки.
- •31. Нормированное ур-ие пл-ти. Приведение общего ур-ия пл-ти к нормированному виду. Расстояние от точки до пл-ти.
- •32. Прямая в пространстве как линия пересечения двух пл-тей. Канонические и параметрические ур-ия. Ур-ия прямой, проходящей через две заданные точки.
- •33. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых. Исследование взаимного расположения двух прямых в пространстве.
- •Преобразование матрицы линейного оператора при переходе к новому базису.
Понятие матрицы. Осн. Операции над матрицами. Сложение матриц и умножение матрицы на число. Св-ва этих операций.
Матрицей назыв. прямоуг. табл. чисел, содержащая произвольное число m строк и произв. число n столбцов. В случае, если m = n, матрица назыв. квадратной, а число m = n - ее порядком.
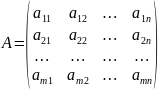
Основными арифметическими операциями над матрицами являются умножение матрицы на число, сложение и умножение матриц.
Сложение
матриц:
суммой двух матриц, например: A
и B,
имеющих одинаковое количество строк и
столбцов, иными словами, одних и тех же
порядков m
и n
назыв.
матрица С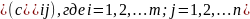 тех же порядков m
и n,
эл-ты
тех же порядков m
и n,
эл-ты
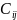 имеют
вид
имеют
вид
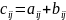 .
C
= A+B.
Св-ва:
1.
Переместительное A+B=B+A;
2.
Сочетательное (А+В)+С=А+(В+С); 3.
Существование нулевой матрицы (все
эл-ты равны 0);
4.
Для
.
C
= A+B.
Св-ва:
1.
Переместительное A+B=B+A;
2.
Сочетательное (А+В)+С=А+(В+С); 3.
Существование нулевой матрицы (все
эл-ты равны 0);
4.
Для
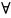 A
A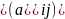 cуществует
противоположная ей матрица. -A
cуществует
противоположная ей матрица. -A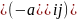 ,
A+(-A)=0
,
A+(-A)=0
Умножение
матрицы на число:
Произведением матрицы
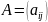 ,
на
вещественное число λ
назыв. матрица
,
на
вещественное число λ
назыв. матрица
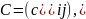 элементы которой равны
элементы которой равны
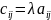 ,
C
= λA
или C =
Aλ.
,
C
= λA
или C =
Aλ.
Св-ва: 1. распределительное λ(A + B) = λA + λB;2. сочетательное (λµ) A =λ (µA);3. распределительное относительно суммы чисел (λ+µ) A = λA + µA.
Понятие матрицы. Осн. Операции над матрицами. Умножение матриц и транспонирование матриц. Св-ва этих операций.
Матрицей назыв. прямоуг. табл. чисел, содержащая произвольное число m строк и произв. число n столбцов. В случае, если m = n, матрица назыв. квадратной, а число m = n - ее порядком.
Основными арифметическими операциями над матрицами являются умножение матрицы на число, сложение и умножение матриц.
Умножение
матриц:
Произведением матрицы
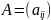 ,
имеющей
порядки соответственно равные m
и
n,
на матрицу
,
имеющей
порядки соответственно равные m
и
n,
на матрицу
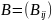 ,
имеющую порядки соответственно равные
n
и
p,
называется матрица
,
имеющую порядки соответственно равные
n
и
p,
называется матрица
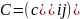 ,
имеющая порядки, соответственно равные
m
и
p,
и элементы
,
имеющая порядки, соответственно равные
m
и
p,
и элементы
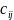 ,
определяемые формулой
,
определяемые формулой
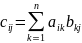 ,
C = AB.
,
C = AB.
Св-ва: 1. сочетательное: (AB) C = A (BC); 2. распределительное относительно суммы матриц: (A + B) C = AC + BC или A (B + C) = AB + AC; 3. перестановочное: лишь для квадратных матриц одинакового порядка.
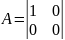 ,
,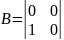 ,
то
,
то
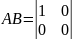 ,
а
,
а
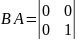 .
.
Транспонирование
матриц:
операция, в результате которой меняются
местами строки и столбцы с сохранением
порядка их следования. В результате
транспонирования матрицы A
получается матрица, называется матрица,
называемая транспонированной по
отношению к матрице A
и обозначается символом
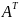 .
.
А
=
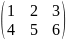 =
=
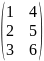 Св-ва:
1.
Св-ва:
1.
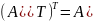 ;
2.
;
2.
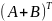 =
=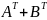 ;
3.
;
3.
 ;
4.
;
4.
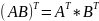
Определители 2-ого и 3-его порядков. Понятие определителя n-порядка.
Определитель
2-ого порядка, при n=2 => det
A
= ∆ =
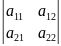 =
=
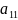 *
*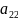 -
-
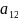 *
* .
Если n=3, то определителем 3-его порядка
наыв. число, равное det
A
=
.
Если n=3, то определителем 3-его порядка
наыв. число, равное det
A
=
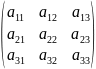 = (
*
= (
*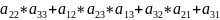 )-(
)-(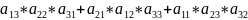 ).
Каждый член определителя 2-ого
порядка
состоит из двух множителей, содержащихся
по одному в каждой строке и в каждом
столбце; при чём все произведения такого
вида входят в этот определитель. Все
члены определителя 3-его
порядка
состоят из трёх множителей, содержащихся
по одному в каждой строке и каждом
столбце; при чём все произв. такого вида
входят в этот определитель. Аналогично,
что каждый член n-порядка
состоит из n-множителей, содержащихся
по одному в каждой строке и в каждом
столбце; при чём все произведения
подобного вида должны являться членами
определителя n-порядка.
).
Каждый член определителя 2-ого
порядка
состоит из двух множителей, содержащихся
по одному в каждой строке и в каждом
столбце; при чём все произведения такого
вида входят в этот определитель. Все
члены определителя 3-его
порядка
состоят из трёх множителей, содержащихся
по одному в каждой строке и каждом
столбце; при чём все произв. такого вида
входят в этот определитель. Аналогично,
что каждый член n-порядка
состоит из n-множителей, содержащихся
по одному в каждой строке и в каждом
столбце; при чём все произведения
подобного вида должны являться членами
определителя n-порядка.
Определителем
n-порядка
соответствующей матрицы А, назыв. число
det
A
= ∆ =
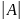 =
=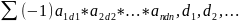 где
суммирование ведётся по всем перестановкам
вторых индексов, ad – чётность перестановки
этих индексов.
где
суммирование ведётся по всем перестановкам
вторых индексов, ad – чётность перестановки
этих индексов.
Св-ва определителей.
Св-во 1. Определитель не меняется при транспонировании. Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).
Св-во 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
Св-во 3. От перестановки двух строк определитель меняет свой знак.
Св-во 4. Определитель, содержащий две одинаковые строки, равен нулю.
Св-во 5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.
Св-во 6. Определитель, содержащий две пропорциональные строки, равен нулю.
Св-во 7. Если все элементы i-й строки определителя n-го порядка представлен в виде суммы двух слагаемых: aij=bj+cj, j = 1, n, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданом определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
Св-во 8. Если одна из строк определителя есть линейная комбинация его других строк, то определитеь равен нулю..
Св-во 9. Определитель не меняется, если к одной из его строк прибавляется любая линейная комбинация других строк.
