Уравнения равновесия жидкости, заключенной в тетраэдре, в проекциях на оси координат имеют вид

(2.1)

Перепишем первое из уравнений (2.1), выразив поверхностные силы через гидростатические давления на соответствующие грани тетраэдра

. (2.2)

Разделив каждый член этого уравнения на площадь S_x = dydz/2 грани, лежащей в координатной плоскости У0Z и являющейся проекцией наклонной грани на эту же плоскость, т.е. S_x = S_нcos γ, получим

. (2.3)

При стягивании объема тетраэдра в точку последний член уравне­ния, содержащий множитель dx, также стремится к нулю, а давления p_x и р_н остаются величинами конечными.

Следовательно, в пределе p_x – р_н = 0 или p_x = р_н.

Поступая аналогично с остальными двумя уравнениями (2.1), получим p_y = р_н и p_z = р_н. Таким образом, окончательно можем записать

. (2.4)

Так как размеры тетраэдра dx, dy и dz взяты произвольно, то наклон площадки S_н также произволен. Следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково.

Рассмотренное свойство давления в покоящейся жидкости имеет место также при движении невязкой жидкости. При движении же реальной вязкой жидкости возникают касательные напряжения и поэтому давление в реальной жидкости указанным свойством не обладает.

2.2. Основное уравнение гидростатики

Рассмотрим распространенный частный случай покоя жидкости, когда на нее действует лишь одна массовая сила  сила тяжести. Пусть жидкость находится в сосуде (рис.2.3), покоящемся относительно Земли. Принимая размеры сосуда существенно меньшими, чем поверхность Земли, можем считать свободную поверхность плоской и гори­зонтальной.

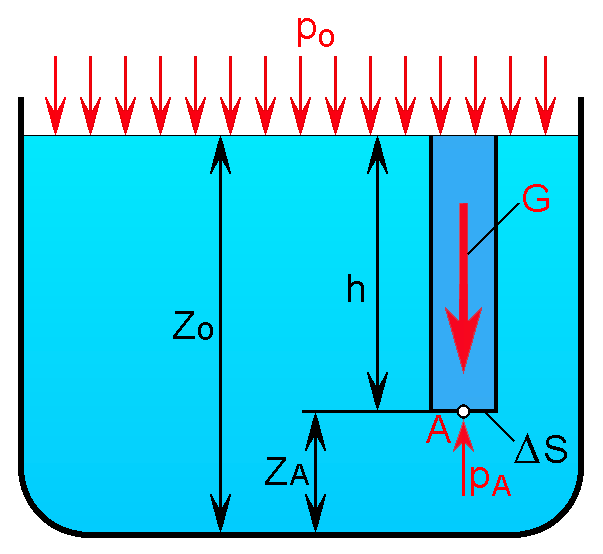
Рис.2.3. Схема к выводу основного уравнения гидростатики

На свободную поверхность действует давление р₀ как результат действующих на нее поверхностных сил. Найдем гидростатическое давление р_А в произвольно взятой точке А, расположенной на глубине h.

Выделим около точки А горизонтальную площадку S и построим на ней вертикальный цилиндрический объем жидкости высотой h.

Объем цилиндра равен W = Sh, а масса - m = hS.

Составим уравнение равновесия этого объема, выделенного из общей массы жидкости. Давление жидкости р_А на нижнее основание цилиндра будет теперь внешним и направлено по нормали внутрь объема, т.е. вверх.

Из схемы (рис.2.3) в проекции на вертикаль имеем

. (2.5)

Последний член этого уравнения представляет собой вес жидкости (силу тяжести) в указанном объеме G= g. Силы давления на боковую поверхность цилиндра в уравнение не входят, т.к. они перпендикулярны к вертикали.

Сократив выражение на S и перегруппировав члены, получим

. (2.6)

Данное уравнение называется основным уравнением гидростатики.

Как видно из уравнения (2.6), давление в точке складывается из двух величин: внешнего давления р₀ на свободную поверхность жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Обратим внимание на следующую особенность.

Поскольку точка А была выбрана произвольно, то можно заключить, что внешнее давление р₀ передается всем точкам этого объема жидкости и по всем направлениям одинаково. Это положение носит название закона Паскаля.

Из формулы (2.6) видно, что давление жидкости возрастает с уве­личением глубины прямо пропорционально, и на данной глубине есть величина постоянная. Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (изобарической поверхностью). Для рассмотренного частного случая (рис.2.3) поверхностями уровня являются горизонтальные плоскости, включая и свободную поверхность.

Уравнение (2.6) можно представить в ином виде, взяв за начало отсчета вертикальной координаты не свободную поверхность рассматри­ваемого объема жидкости (рис.2.6), а произвольную горизонтальную плоскость, например, дно сосуда.

Обозначит через Z_A координату точки А, через Z₀  координату свободной поверхности и заменив в уравнении h на Z₀  Z_A, можем записать

или . (2.7)

Разделив вcе члены последнего уравнения на g, получим

. (2.8)

Поскольку точка А была взята произвольно, имеем для всего расс­матриваемого неподвижного объема жидкости , где р_i и Z_i  соответственно, давление и вертикальная координата любой i-той точки.

Координата Z называется геометрической высотой.

Составляющая вида р/g имеет линейную размерность и называется пьезометрической высотой.

Сумму геометрического и пьезометрического напоров можно интерпретировать как полный напор в точке покоящейся жидкости (иногда ее называют гидростатическим напором).

Таким образом, полный напор есть величина постоянная для всего объема неподвижной жидкости.

Пьезометрическую высоту, соответствующую избыточному давлению, можно определить по пьезометру, который представляет собой вертикальную стеклянную трубку (рис.2.4, а). Верхний конец трубки открыт в атмосферу, а нижний присоединен к сосуду, в котором измеряется давление.

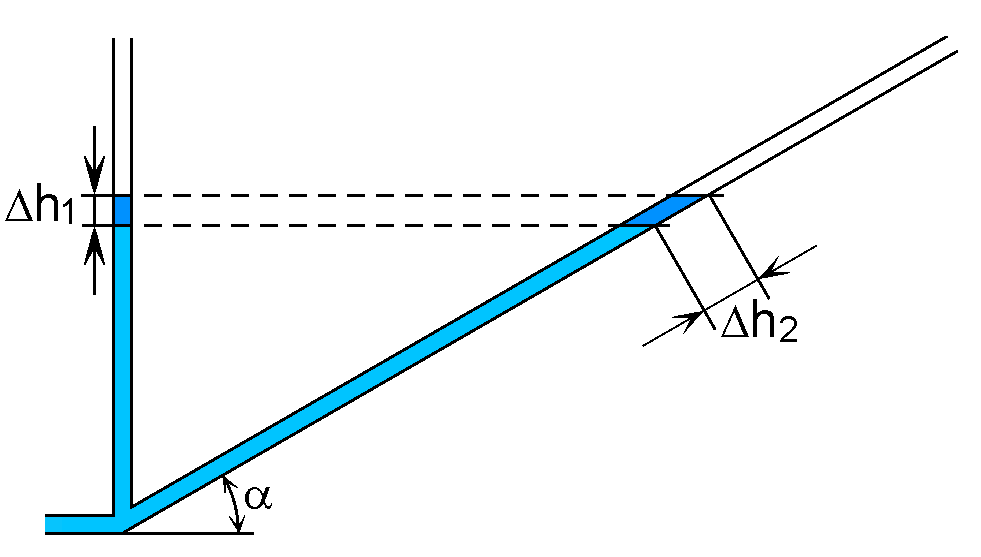
Рис. 2.4. Измерение давления при помощи пьезометра

Применяя формулу (2.6) к жидкости, находящейся в пьезометре, будем иметь

, (2.9)

где р – давление в жидкости на уровне присоединения пьезометра; р_атм – атмосферное давление.

Отсюда высота подъема жидкости в пьезометре

, (2.10)

где  избыточное давление на уровне присоединения пьезометра.

Очевидно, что если на свободную поверхность покоящейся жидкости действует атмосферное давление, то пьезометрическая высота для любой точки рассматриваемого объема жидкости равна глубине расположения этой точки.

Для повышения точности измерений пьезометрическую трубку устанавливают наклонно (рис. 2.4, б). Так, если угол  равен 30⁰ , то .

Часто давление в жидкостях и газах численно выражают в виде соответствующей этому давлению пьезометрической высоты.

Например, для воды имеем м водяного столба. При р = 0,1 МПа = 1кгс/см² = 10 м вод.ст.

Рис. 2.5. Схема образования вакуума под поршнем

Если абсолютное давление в жидкости или газе меньше атмосферного, то говорят, что имеет место разряжение, или вакуум.

За величину вакуума принимается недостаток до атмосферного давления:

или . (2.11)

Возьмем трубу с плотно подогнанным к ней поршнем. Опустим нижний конец трубы в сосуд с жидкостью и будем постепенно поднимать поршень (рис.2.5). Жидкость будет следовать за поршнем и вместе с ним поднимется на некоторую высоту от свободной поверхности с атмосферным давлением. Так как для точек, расположенных под поршнем, глубина погружения относительно свободной поверхности отрицательна, то под поршнем имеем вакуум .

По мере подъема поршня давление жидкости под ним уменьшается. Нижним пределом снижения давления для жидкости является давление насыщенного пара. Поэтому максимальная высота всасывания без нарушения сплошности среды составит .

При нормальном атмосферном давлении (0,1033 МПа) максимальная высота всасывания для воды равна м, для бензина (= 750 кг/м³) – 13,8 м, а для ртути – 0,76 м.

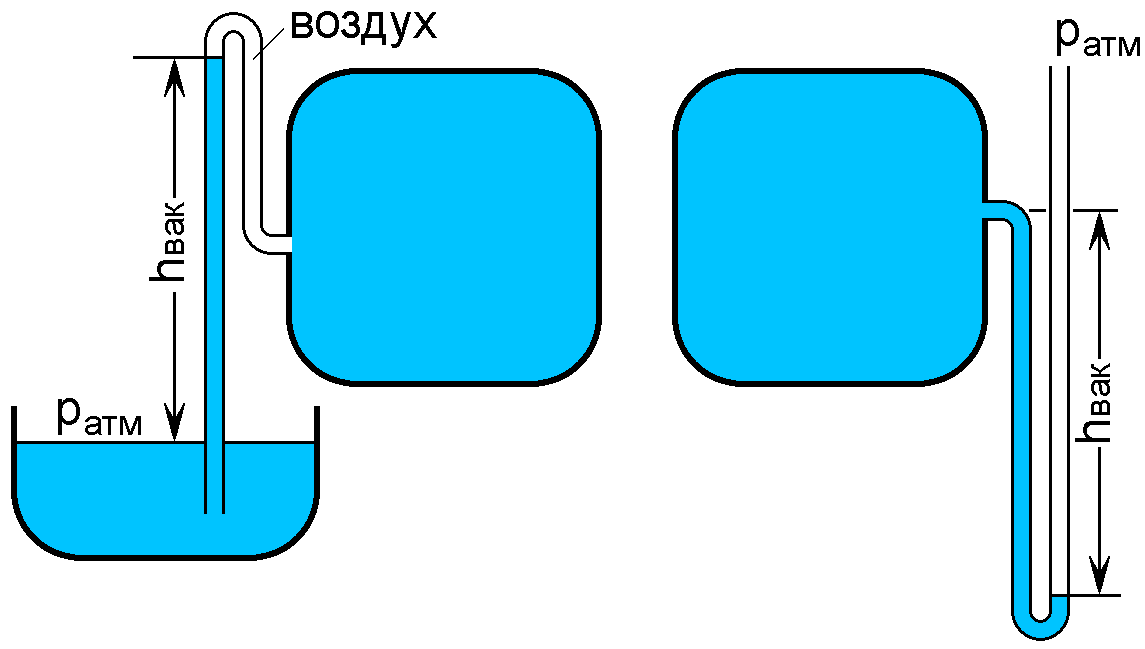
Рис. 2.6. Схемы измерения вакуума

Простейшим устройством для измерения вакуума может служить U  образная трубка, показанная на рис. 2.6 в двух вариантах.

Для измерения давления жидкостей и газов в лабораторных условиях помимо пьезометра используются жидкостные и механические манометры. На рис.2.7 показаны схемы жидкостных манометров.

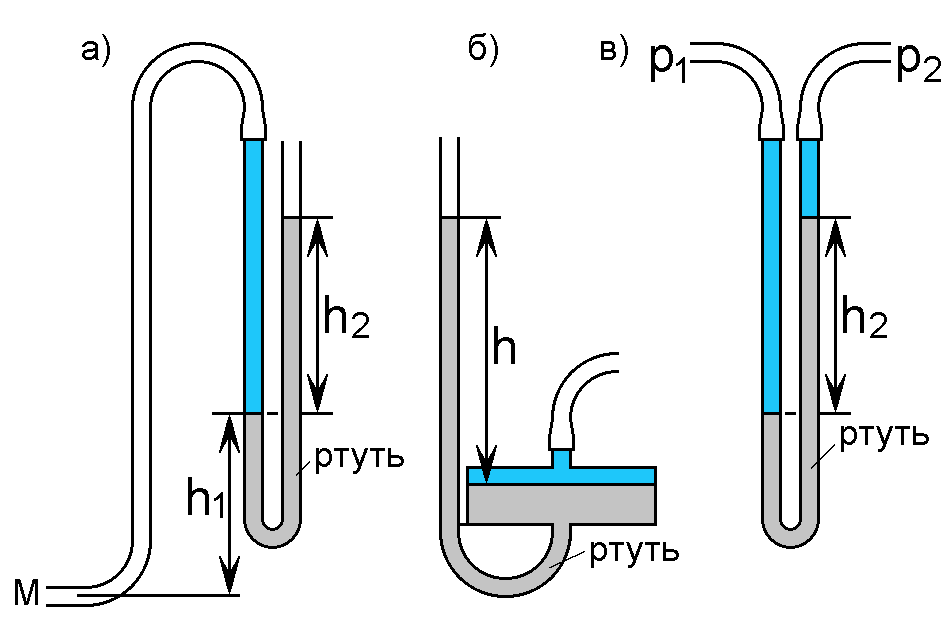
Рис.2.7 Схемы жидкостных манометров

Так называемый U – образный манометр (рис.2.7, а) представляет собой изогнутую стеклянную трубку, содержащую ртуть (чем больше плотность используемой жидкости в манометре, тем большее давление можно измерить).

При измерении небольших давлений газа вместо ртути используют спитр, воду и иногда тетрабромэтан.

Если измеряется давление жидкости в точке М, и соединительная трубка заполнена этой же жидкостью, то следует учитывать высоту расположения манометра над точкой М.

Так, избыточное давление в точке М равно

. (2.12)

Чашечный манометр (рис.2.7, б) удобнее описанного выше тем, что можно фиксировать только одно положение уровня жидкости, т.к. при достаточно большом диаметре чашки по сравнению с диаметром трубки уровень жидкости в чашке можно считать неизменным.

На рис.2.7, в показан манометр для измерения разности давлений. . (2.13)