Тогда исходное выражение уравнения Бернулли примет вид

. (6.44)

Применим закон об изменении количества движения к фиксированному объему, заключенному между сечениями 1-1, 2-2 и стенкой трубы. Для этого определим равнодействующую внешних сил, действующих на этот объем в направлении движения, т.е. от сил давления. Учитывая третье допущение, получим равнодействующую силу, численно равную секундному импульсу

Соответствующее этому импульсу изменение количества движения находится как разность между секундным количеством движения, выносимым из рассматриваемого объема и вносимым в него. При равномерном распределении скоростей по сечениям эта разность равна

Приравнивая одно к другому, получим

.

Заменим расход через его выражение Q = V₂ S₂ и разделим обе части этого выражения на S₂pg:

или .

Преобразуем правую часть этого уравнения

и перегруппируем его члены

.

Сопоставляя полученное выражение с формулой (6.44), можем сде­лать вывод, что

, (6.45)

т.е. потеря напора при внезапном расширении потока равна скоростному напору, определенному по разности скоростей. Это положение называют теоремой Борда, который вывел эту формулу. Полученный результат приводится к общему виду представления потерь на местном сопротивлении (формуле Вейсбаха) при помощи уравнения постоянства расхода (3.11) .

Исходя из этого можем записать

. (6.46)

Когда площадь S₂ весьма велика (например, выход из трубы в боль­шой резервуар) по сравнению с площадью S₁, и следовательно, скорость V₂ можно считать равной нулю, потеря напора на расширении составит

,

т.е. V = 1, т.к. теряется весь скоростной напор.

Доказанная теорема хорошо подтверждается опытом при турбулентном течении и широко используется в практических расчетах.

В заключение отметим, что при ламинарном режиме течения закон сопротивления является еще более сложным и исследован в меньшей степени, чем при турбулентном режиме течения. Если при турбулентном течении потери на местном сопротивлении с достаточной степенью точности можно считать пропорциональными скорости во второй степени, а коэффициенты потерь , определяются в основном формой местного сопротивления и практически не зависят от Re, то при ламинарном течении потерю напора h_M следует представлять как сумму

, (6.47)

где h_тp  потеря напора, обусловленная непосредственным действием сил вязкости в данном местном сопротивлении и скорости в первой степени; h_вихр потеря напора, связанная с деформацией потока и вихреобразованием в самом местном сопротивлении или за ним и пропорциональная квадрату скорости.

Так, например, при течении через колиброванное отверстие (жиклер) (рис.6.20) слева от плоскости расширения возникает потеря напора на вязкостное трение, а справа  на вихреобразование.

Рис.6.20. Схема жиклера

Учитывая закон сопротивления при ламинарном течении с поправкой на начальный участок, а также формулу Вейсбаха, выражение можно представить в виде

, (6.48)

где А и В  безразмерные константы, зависящие в основном от формы местного сопротивления.

5.4. Общие сведения о гидравлических потерях

Потери удельной энергии (напора) или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней.

Механизм действия сил сопротивления очень сложен. Аналитически пока не удалось получить универсальные соотношения для их вычисления. Поэтому при расчетах потерь напора используют, как правило, эмпирические зависимости.

Как показывают опыты, в большинстве случаев гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому принят следующий общий способ выражения гидравлических потерь полного напора в виде

. (5.20)

В общем случае показатель степени у V_ср может принимать значение от 1 до 2. Такое выражение удобно тем, что включает в себя безраз­мерный коэффициент пропорциональности ξ, называемый коэффициентом потерь, значение которого для данного русла в определенном приближении может считаться постоянным. Очевидно, что ξ есть отношение потерянного напора к скоростному напору.

Гидравлические потери обычно принято разделять на местные потери и потери по длине русла.

Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, вызывающими деформацию потока, из-за местных изменений формы и размера русла. На рис. 5.4 приведены примеры типичных местных гидравлических сопротивлений.

При протекании жидкости через местные сопротивления изменяется ее скорость, и обычно возникают крупные вихри, которые образуются за местом отрыва потока от стенок. Образуются области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям.

Местные потери напора определяются по формуле (5.20), которую часто называют формулой Вейсбаха. В ней V_cp  средняя по живому се­чению скорость в трубе, в которой установлено данное местное сопро­тивление. При этом, если диаметр трубы и, следовательно, скорость в ней изменяются по длине (рис.5.4,г), то за расчетную скорость удобнее принимать большую из скоростей, т.е. ту, которая соответствует меньшему диаметру трубы

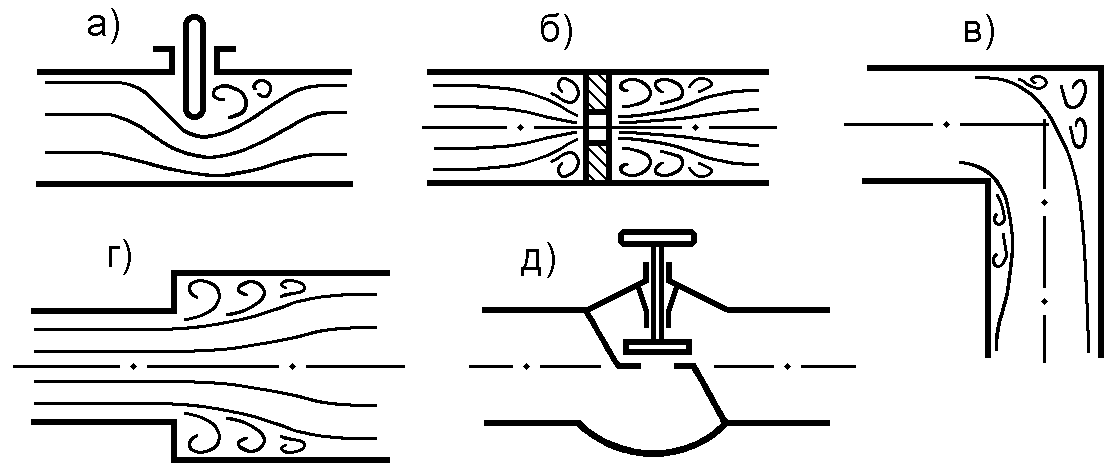
Рис.5.4. Схемы местных гидравлических сопротивлений:

а  задвижка; б  диафрагма; в  колено; г  внезапное расширение;

д – вентиль

В дальнейшем местные потери будем обозначать через h_м.

Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления ξ, которое определяется экспериментально и только в ряде частных случаев имеется теоретическое решение.

Потери напора по длине  это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают пропорционально длине трубы. Эти потери обусловлены внутренним трением жидкости (вязкостью), а потому имеют место не только в шероховатых, но и в гладких трубах.

Потери напора по длине можно рассчитывать по общей формуле (5.20), однако удобнее коэффициент ξ, связать с относительной длиной трубы, т.е. представить в виде

, (5.21)

где λ - коэффициент сопротивления участка трубы длиной, равной его диаметру.

Тогда формула (5.20) примет вид

. (5.22)

Эту формулу обычно называют формулой Вейсбаха - Дарси, а безразмерный коэффициент λ - коэффициентом потерь на трение по длине, или коэффициентом Дарси.

Для выяснения физического смысла коэффициента Дарси рассмотрим равномерное движение в трубе объема жидкости цилиндрической формы длиной 1 и диаметром d, равном диаметру трубы. Составим уравнение сил, действующих на объем - сил давления и силы трения:

,

где _о  напряжение трения на стенке трубы.

Отсюда

. (5.23)

С другой стороны, из (5.22) имеем

. (5.24)

Приравнивая (5.23) и (5.24), получим

. (5.25)

Таким образом, коэффициент Дарси есть величина, пропорциональная отношению напряжения трения на стенке трубы к динамическому давлению, определенному по средней скорости.

Ввиду постоянства объемного расхода несжимаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются постоянными, несмотря на наличие гидравлических потерь. Потеря напора в этом случае приводит к снижению пьезометрического напора.