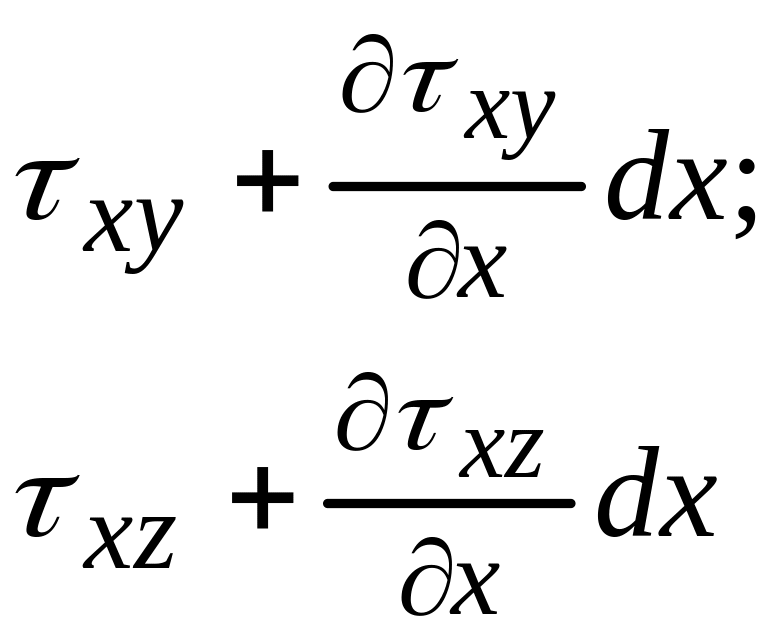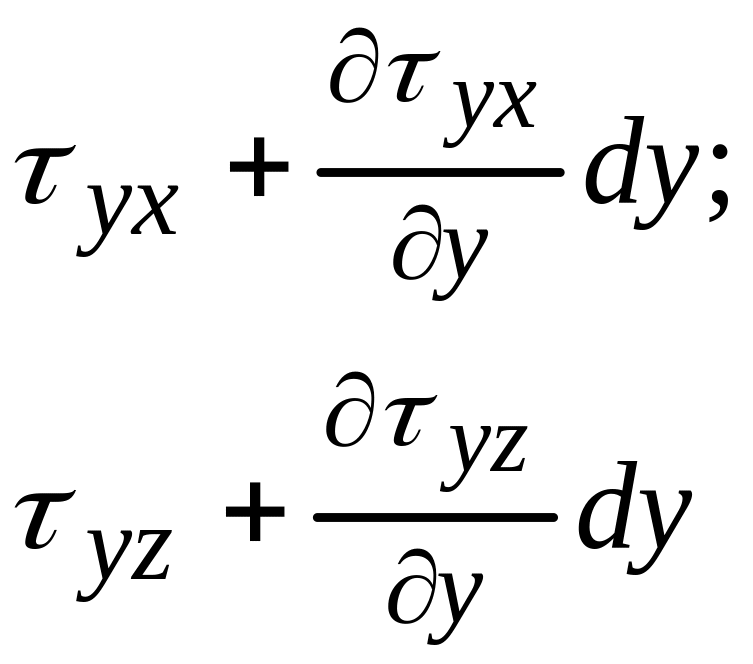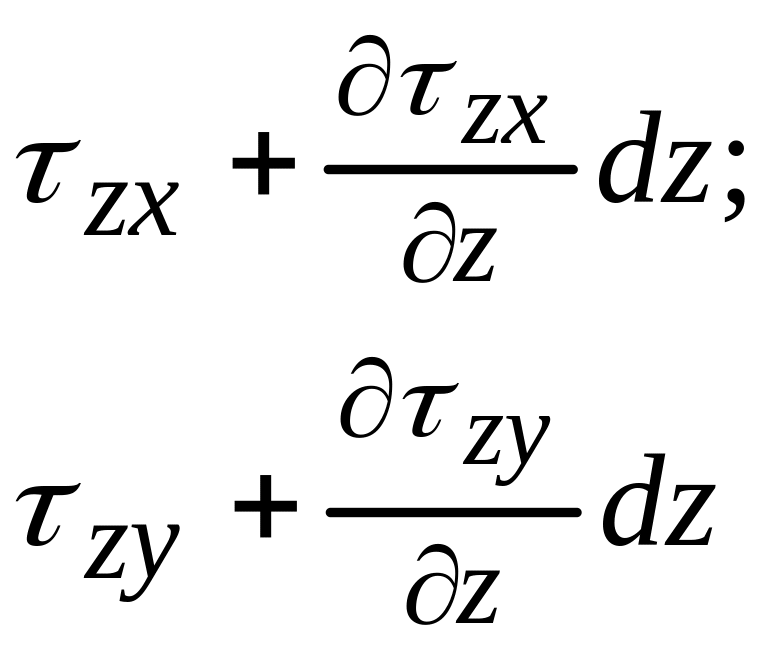Отсюда . Тогда решение интеграла имеет вид:

.

После преобразований получим

.

С практически небольшой погрешностью решение интеграла запишем в виде

.

Тогда уравнение (4.17) запишется как

. (4.19)

Имея в виду уравнение Клайперона (1.14) выражение (4.19) можем переписать

(4.20)

Следовательно, при больших перепадах давления и температуры по длине струйки полная удельная энергия равна сумме потенциальной, кинетической и тепловой (последнее слагаемое в (4.20)) энергии.

Уравнения (4.18) и (4.20) являются основными при исследованиях и расчетах установившегося движения сжимаемого невязкого газа.

Контрольные вопросы

1. Чем отличается модель «невязкая жидкость»?

2. Каков смысл преобразований уравнений Эйлера, выполненных Громекой, и представления этих уравнений в форме, данной Громекой? Запишите уравнения Эйлера—Громеки.

3. Какой вид имеет уравнение движения невязкой жидкости вдоль ли­нии тока?

4. Как записывается уравнение Бернулли для элементарной струйки невязкой несжимаемой жидкости, если из массовых сил действует только сила тяжести?

5. Как изменяется уравнение Бернулли по сравнению с предыдущим случаем, если на жидкость помимо силы тяжести действуют и силы инерции?

6. Что такое удельная энергия?

7. Какой физический закон выражает уравнение Бернулли?

8. Что такое пьезометрический, скоростной и полный напор? Как они изменяются по длине (вдоль направления движения)?

9. Справедливо ли уравнение Бернулли на линиях тока?

ЛЕКЦИЯ 5. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ (ПРОДОЛЖЕНИЕ). НАПРЯЖЕНИЯ В ДВИЖУЩЕЙСЯ ВЯЗКОЙ ЖИДКОСТИ. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ СТРУЙКИ ВЯЗКОЙ ЖИДКОСТИ ПРИ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА ПРИ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ ВЯЗКОЙ ЖИДКОСТИ. УДЕЛЬНАЯ ЭНЕРГИЯ ПОТОКА. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА.

Динамика вязкой жидкости

При движении вязкой жидкости в ней возникают не только нормальные, но и касательные напряжения, т.к. вязкая жидкость обладает способностью оказывать сопротивление относительному сдвигу своих слоев и частиц. Нормальные и касательные напряжения в вязкой жидкости зависят не только от координат точек жидкости. В данной точке жидкости напряжения зависят от направления действия или, иначе, от ориентации в пространстве площадки, на которую они действуют.

Напряжения в движущейся вязкой жидкости

Рассмотрим элементарный объем в виде параллелепипеда с ребрами dx,dy,dz, который выделим из движущейся жидкости (рис. 5.1).

Обозначим напряжения на гранях, ближайших к началу координат (АВКЕ, AEHD, ABCD), через р_хх, р_уу, p_zz, _xy, _xz, _yx, _yz, _zx, _zy.

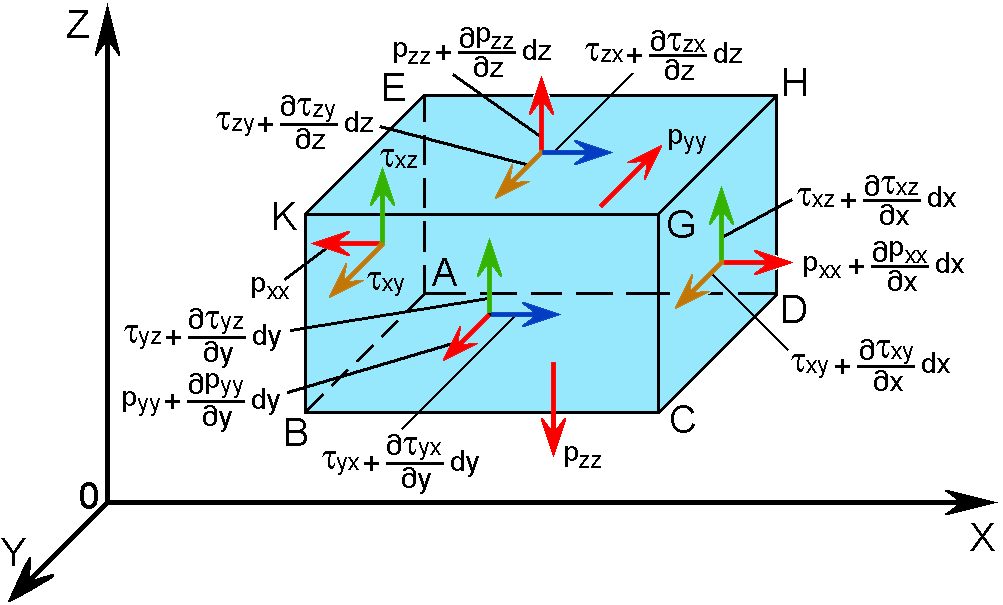
Рис.5.1. Схема действия напряжений в движущейся

вязкой жидкости

Первый индекс указывает ось, которой перпендикулярна данная грань, т.е. направление нормали к граням, второй  направление дейс­твия напряжения, т.е. параллельно какой оси координат оно направлено. Так, касательное напряжение _yx действует на грани, перпендикулярной оси OY, в направлении оси ОХ; _zx действует на грани, перпен­дикулярной оси OZ, в направлении оси ОХ и т.д.

Считая напряжения непрерывно изменяющимися по объему жидкости, получим значения напряжений на всех гранях параллелепипеда, пользуясь разложением функций напряжения в ряд Тейлора (табл. 5.1).

Отметим, что в любой точке потока вязкой жидкости касательные напряжения на взаимно перпендикулярных площадках, направленные по нормали к линии пересечения этих площадок, равны друг другу, т.е.

_xy = _yx ; _xz = _zx ; _yz = _zy .

Таблица 5.1

Грань	Напряжения
	нормальные	касательные
ABKE
DCGH
AEDH
BKGC
ABCD
EKGH

Таким образом, напряженное состояние вязкой движущейся жидкости характеризуется шестью независимыми компонентами напряжений р_хх, р_уу, p_zz, _xy = _yx ; _xz = _zx ; _yz = _zy.

Составим уравнения движения массы жидкости, заключенной в параллелепипеде (рис .5.1), рассмотрев сначала сумму проекций сил на направление оси ОХ. Эта сумма равна произведению массы параллелепипеда dxdydz на проекцию ускорения движения его полюса (центра).

При составлении проекций принято считать направления нормальных напряжений совпадающими с направлениями внешних нормалей к граням параллелепипеда. В проекции на ось ОХ уравнение движения имеет вид

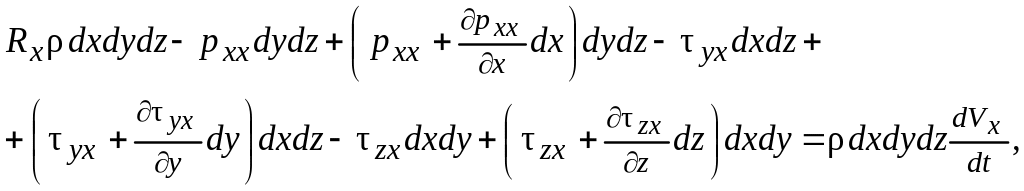
где R_xdxdydz  проекция равнодействующей массовых сил на ось ОХ.

Произведя сокращения подобных членов, получим

.

Выполнив аналогичные действия для проекций сил на направления осей OY и OZ, получим систему дифференциальных уравнений движения вязкой жидкости в напряжениях:

(5.1)

Если считать заданными проекции плотности распределения массовых сил, в уравнение (5.1) входят десять неизвестных функций: V_x, V_y, V_z, p_хх, p_yy, p_zz, _xy = _yx , _xz = _zx, _yz = _{zy .}

Так как уравнений движения всего три, то система уравнений дви­жения вязкой жидкости оказывается незамкнутой. Замыкание этой систеы уравнений может быть осуществлено с помощью уравнения неразрывности и других соотношений, устанавливающих связи между неизвестными. Обычно эти соотношения вводятся на основе гипотез и потому обязательно должны быть подтверждены экспериментально.

В основу получения соотношений между касательными напряжениями t и скоростями деформации жидких частиц в гидромеханике положен закон внутреннего трения Ньютона (1.18)

.

где µ  динамический коэффициент вязкости;  градиент скорости по нормали к направлению движения.

Градиент скорости при слоистом движении жидкости выражает скорость угловой деформации частицы:

, т.е. .

Распространяя закон вязкого трения на трехмерное (пространствен­ное) движение, получим для касательных напряжений:

(5.2)

В каждой точке движущейся вязкой жидкости кроме касательных напряжений есть нормальные напряжения, значения которых зависят от направления действия. Последние являются следствием проявления вязкости и в гидромеханике описываются зависимостями

(5.3)

где р  давление, аналогичное давлению, действующему в невязкой жидкости,  добавочные нормальные напряжения от действия сил вязкости.

Добавочные напряжения не зависят от значения давления, но зави­сят от направления действия.

Перепишем уравнения (5.1), объединив в скобках все члены, зави­сящие от вязкости:

Подставив в эту систему уравнений значения напряжений из (5.2) и (5.3),а также выразив субстанциональное ускорение через локальное и конвективное ускорения (см. 3.4), получим систему уравнений движения вязкой несжимаемой жидкости ( = const) в виде:

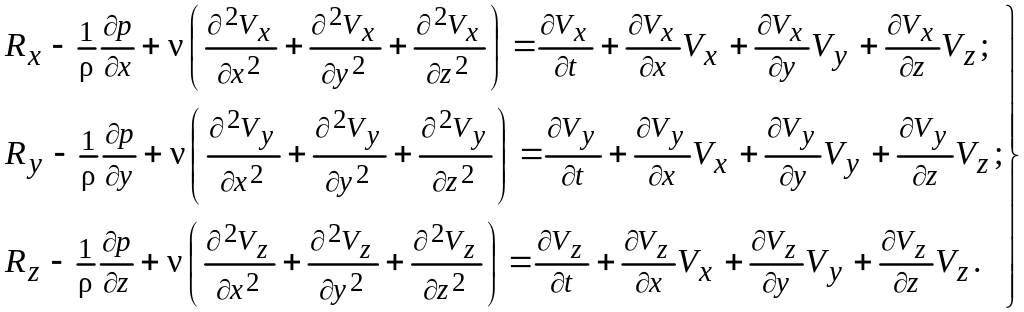(5.4)

где ν - кинематический коэффициент вязкости.

Эти уравнения носят название уравнений Навъе-Стокса. Они записаны для неустановившегося движения несжимаемой вязкой жидкости.

Составляющие плотности распределения массовых сил R_x, R_y, R_z считаются заданными, а плотность  и кинематическая вязкость ν ( при соответствующем обосновании)  постоянными.

Тогда полученные уравнения совместно с уравнением неразрывности образуют замкнутую систему: при четырех уравнениях имеем четыре неизвестных функции p, V_x, V_y, V_z.

Общее решение нелинейных дифференциальных уравнений Навье-Стокса пока не найдено. Но в ряде случаев получены частные решения. Для этого должны быть заданы начальные и граничные условия.

Начальными условиями обычно задается распределение скоростей в области движения жидкости в некоторый момент времени. Это обычно удается практически осуществить только на основе экспериментальных данных.

Граничные условия задаются значениями скорости и давления на границах потока. На твердой границе используется условие прилипания частиц жидкости к твердому телу, т.е. например, на неподвижной твердой границе скорость потока будет равна нулю.

Границей потока может служить и свободная поверхность. В этом случае граничным условием является: давление во всех точках свободной поверхности одинаково и равно давлению во внешней среде.