6.4. Ламинарное течение

Как отмечалось выше, ламинарное течение характеризуется парал­лельно-струйчатым упорядоченным движением частиц жидкости. Движение можно представить как совокупность бесконечно тонких кольцевых концентрических слоев, перемещающихся относительно друг друга. Единственным источником потерь энергии в данном случае является трение между слоями движущейся жидкости, подчиняющееся закону трения Ньютона.

Рассмотрим установившееся ламинарное течение жидкости в прямой круглой трубе с внутренним диаметром d = 2r. Расположим трубу горизонтально. Этим мы исключим влияние силы тяжести и упростим вывод. Достаточно далеко от входа в трубу, где поток стабилизировался, выделим участок длиной 1 двумя сечениями 1-1 и 2-2 (рис.6.5).

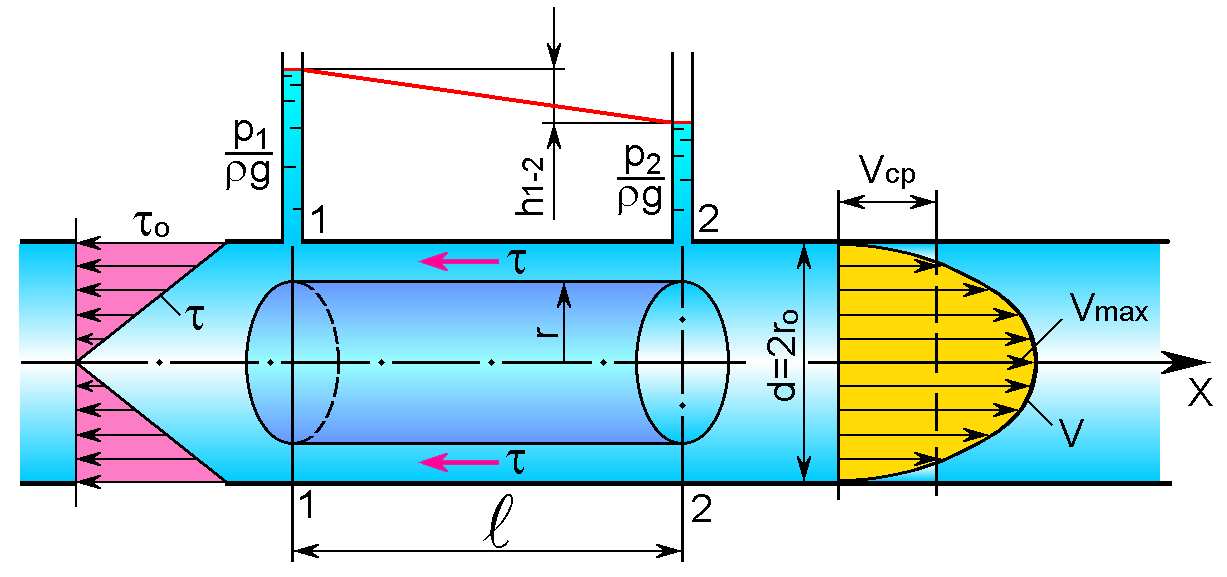
Рис.6.5. Схема к теории ламинарного течения жидкости в трубе

Запишем уравнение Бернулли для выделенного участка. Согласно (5.16) имеем

. (6.14)

Вследствие неизменности диаметра трубы и стабильности потока V₁ =V₂ и L₁ = L₂ . Так как труба горизонтальная, то z₁ = z₂. Отсюда выра­жение (6.14) примет вид

.

Тогда потери на трение по длине составят

. (6.15)

Выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Составим уравнение равномерного движения этого объема, т.е. равенство нулю суммы сил, действующих на объем. Такими силами являются силы давления и вязкости. Обозначая через  касательные напряжения на боковой поверхности цилиндра, получим

.

Из этой формулы касательные напряжения определяются как

, (6.16)

т.е. они изменяются по линейному закону в функции радиуса.

Эпюра касательных напряжений приведена на рис.6.5. Отметим, что эта эпюра не зависит от режима течения жидкости.

В свою очередь, согласно формуле (1.18) касательные напряжения для рассматриваемого случая описываются выражением

. (6.17)

В этом выражении переменная у (расстояние от стенки) заменена текущим радиусом r. Знак минус обусловлен тем, что направление отс­чета у (от стенки) противоположно направлению отсчета r (от оси).

Приравнивая выражения (6.16) и (6.17), получим .

Отсюда приращение скорости составит .

Проинтегрировав это выражение, будем иметь .

Постоянная интегрирования находится из граничных условий.

При r = r_о имеем V = 0 и .

Тогда формула скорости по окружности радиусом r имеет вид

. (6.18)

Это выражение является законом распределения скоростей по живому сечению круглой трубы при ламинарном режиме течения. Кривая, изображающая эпюру скоростей, представляет собой квадратичную параболу (рис.6.5).

Максимальная скорость частиц жидкости будет на оси трубы (г = 0)

. (6.19)

Расход через элементарную площадку dS составит dQ = VdS, или согласно (6.18) и dS = 2πrdr будет

Проинтегрировав это выражение от r = 0 до r = r_о, т.е. по всей площади живого сечения, получим

и . (6.20)

Средняя скорость по живому сечению составит

. (6.21)

Сравнивая между собой формулы (6.19) и (6.21), получим

Зная закон распределения скоростей по сечению потока, можно оп­ределить величину коэффициента кинетической энергии – коэффициента Кориолиса.

Подставим в формуле (5.14) среднюю скорость по выражению (6.21) и V_i по формуле (6.18).

Тогда

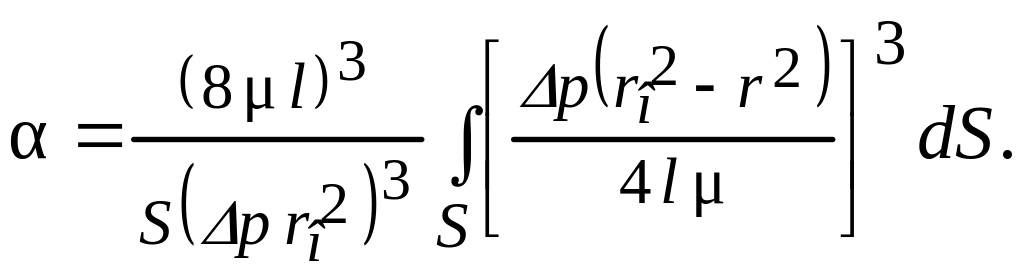
Имея в виду, что и , получим

Таким образом, действительная кинетическая энергия потока при ламинарном режиме течения в два раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.

Определим зависимость потерь напора h_1-2 на трение от параметров потока.

Для этого из выражения (6.20) определим перепад давления р:

.

Имея в виду, что µ= ν и r_о = d/2, а также согласно. (6.15) получим

(6.22)

Эта формула получена Пуазейлем и носит его имя. С ней полностью согласуется формула (6.12), представляя ее другой вид.

Формула (6.22) широко используется для расчета трубопроводов с ламинарным режимом течения.

В 5.4 потери по длине трубы представлены в виде зависимости от средней скорости по формуле Вейсбаха-Дарси (5.22).

Для приведения формулы (6.22) к подобному виду заменим в ней расход Q его выражением через среднюю скорость

Тогда

(6.23)

Из этого выражения видно, что при ламинарном режиме течения жидкости потери действительно пропорциональны скорости в первой степени, как утверждали Гаген и Пуазейль.

Для окончательного приведения формулы потерь на трение по длине (6.23) к виду формулы Вейсбаха-Дарси (5.22) приравниваем их

Отсюда коэффициент Дарси для ламинарного потока (_л) будет

или имея в виду , получим , и окончательно

(6.24)

Как уже отмечалось, при установившемся ламинарном движении линии тока и траектории жидких частиц совпадают и это  прямые, параллельные направлению движения.

Если направить ось ОХ ортогональной системы координат XYZ вдоль оси трубы, то проекции скорости частицы жидкости согласно (6.18) будет

где

Видно, что единственная, не равная нулю проекция скорости не за­висит от координаты X. Компоненты угловой скорости по (3.13) составят

(6.25)

Дифференциальное уравнение вихревой линии (3.16)

после подстановки в него (6.25) примет вид и после интегрирования получим

Таким образом, вихревые линии в данном случае представляют собой концентрические окружности с центрами на оси трубы.

Угловая скорость частиц жидкости по (3.14) составит

,

Или . (6.26)