
- •Гидравлика (курс лекций) введение
- •1.1 Жидкости и их физические свойства
- •1.2 Модели жидкости
- •1.3 Силы, действующие в жидкости
- •Плотность распределения касательных сил
- •Контрольные вопросы
- •2.1. Гидростатическое давление и его свойство
- •Уравнения равновесия жидкости, заключенной в тетраэдре, в проекциях на оси координат имеют вид
- •2.2. Основное уравнение гидростатики
- •2.3. Дифференциальные уравнения равновесия жидкости
- •2.4. Решение дифференциальных уравнений равновесия жидкости для ряда частных случаев
- •2.4.1. Равномерное вращение сосуда с жидкостью
- •2.4.2. Прямолинейное движение сосуда с постоянным ускорением
- •После интегрирования получим .
- •2.4.3. Равновесие тела, плавающего на поверхности жидкости
- •Контрольные вопросы
- •Лекция 3. Кинематика жидкости. Общие положения и определения. Расход. Уравнение расхода. Движение жидкой частицы. Понятие о вихревом и потенциальном движении. Ускорение жидкой частицы
- •3.1. Общие положения и определения
- •3.2. Расход. Уравнение расхода
- •3.3. Движение жидкой частицы. Понятие о вихревом и потенциальном движении
- •Угловая скорость будет
- •Дифференциальные уравнения вихревых линий
- •Тогда согласно (3.13) получим
- •3.4. Ускорение жидкой частицы Ускорение жидкой частицы можно представить в виде
- •Контрольные вопросы
- •3.1 Динамика невязкой жидкости
- •3.2 Уравнение бернулли для элементарной струйки идеальной жидкости
- •По аналогии с этим для элемента 2-2' получим
- •Тогда работа силы тяжести будет
- •Разделим это уравнение на dG и произведя сокращения, можем записать
- •4.2. Дифференциальные уравнения движения невязкой жидкости
- •Подставим эти выражения в уравнения вихревой линии
- •4.3. Уравнение бернулли для элементарной струйки невязкого газа
- •Отсюда . Тогда решение интеграла имеет вид:
- •Контрольные вопросы
- •Динамика вязкой жидкости
- •Напряжения в движущейся вязкой жидкости
- •5.2. Уравнение бернулли для элементарной струйки вязкой жидкости при установившемся движении
- •Т.К. Определитель равен нулю из-за пропорциональности первой и третьей строк (см. Уравнение (4.15)). После интегрирования будем иметь
- •Если из массовых сил действует только сила тяжести, получим
- •5.3. Уравнение бернулли для потока при установившемся движении вязкой жидкости
- •5.3.1. Удельная энергия потока
- •Далее можем записать
- •Расход жидкости через живое сечение потока
- •5.3.2. Уравнение бернулли для потока
- •7.1. Режимы течения жидкости в трубах. Опыты рейнольдса
- •6.4. Ламинарное течение
- •Решая совместно (6.26) и (6.21), получим
- •Сопоставляя (6.27) и (6.28), получим , т.Е. Эпюра угловых скоростей частиц аналогична эпюре касательных напряжений.
- •6.4.2. Начальный участок ламинарного течения
- •6.4.3. Ламинарное течение в зазоре
- •Тогда и формула закона распределения скоростей по живому сечению будет иметь вид
- •Тогда формула (1.18) для данного случая примет вид и после интегрирования будет
- •Тогда закон распределения скоростей имеет вид
- •Б) направление движения стенки противоположно течению жидкости (рис.6.10, б).
- •Если поршень расположен в цилиндре с эксцентриситетом е, то зазор а будет переменной величиной (рис.6.11,б):
- •6.5. Турбулентное течение
- • Ламинарный подслой; 2 переходный слой;
- •3 Турбулентное ядро
- •Контрольные вопросы
- •6.6. Местные гидравлические сопротивления
- •Тогда исходное выражение уравнения Бернулли примет вид
- •Учитывая закон сопротивления при ламинарном течении с поправкой на начальный участок, а также формулу Вейсбаха, выражение можно представить в виде
- •5.4. Общие сведения о гидравлических потерях
- •Контрольные вопросы
- •7.1. Истечение через малое отверстие в тонкой стенке при постоянном напоре.
- •В данном случае имеем
- •Множитель называется коэффициентом скорости.
- •Из выражения (7.5) коэффициент расхода равен
- •Исходя из этого уравнения, скорость истечения составит
- •7.2. Истечение через насадки при постоянном напоре
- •7.3. Истечение жидкости из резервуара при переменном напоре
- •Основной задачей, решаемой в этом случае, является определение времени опоражнивания резервуара от уровня н1 до н2.
- •Означает, что с уменьшением z объем вытекшей жидкости увели-чивается; dz - изменение уровня в резервуаре за время dt;
- •Отсюда имеем .
- •Контрольные вопросы
Из выражения (7.5) коэффициент расхода равен
![]() или
или
![]() .
.
Это значит, что коэффициент расхода есть отношение действительного расхода к тому расходу Q* = S0Vи, который имел бы место при отсутствии сжатия струи и сопротивления. Величина Q* не является расходом при истечении идеальной жидкости, т.к. сжатие струи будет иметь место и при отсутствии гидравлических потерь.
Коэффициенты сжатия струи , скорости o и расхода o зависят, в первую очередь, от типа отверстия, а также как и все безразмерные коэффициенты в гидромеханике, от основного критерия гидродинамического подобия для напорных течений - числа Рейнольдса.
При истечении воды
и воздуха, когда обычно имеет место
развитый турбулентный режим движения,
можно принимать
= 0,6 - 0,64;
![]() 0,06;
o=
0,97 - 0,98 и тогда o
= 0,6 - 0,63.
0,06;
o=
0,97 - 0,98 и тогда o
= 0,6 - 0,63.
На практике часто приходится иметь дело не со свободным истечением жидкости, а с истечением в пространство, заполненное этой же жидкостью (рис. 7. 2). Такой случай называется истечением под уровень, или истечением через затопленное отверстие. В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Запишем уравнение Бернулли для участка, ограниченного сечениями 1-1 и 2-2 (рис. 7. 2), где скорости будем считать равными нулю:
![]() ,
,
где V
– скорость истечения в сжатом сечении;
![]()
потери напора
на отверстии;
ξ0
- коэффициент потерь, имеющий примерно
такое же
значение, что и при истечении в атмосферу.
потери напора
на отверстии;
ξ0
- коэффициент потерь, имеющий примерно
такое же
значение, что и при истечении в атмосферу.
Составляющая
![]() является потерей напора, связанной с
внезапным
является потерей напора, связанной с
внезапным

Рис. 7.2 Схема истечения под уровень расширением струи от сжатого состояния до сечения во втором резервуаре
Исходя из этого уравнения, скорость истечения составит
![]() ,
(7.7)
,
(7.7)
где
![]() -
расчетный напор.
-
расчетный напор.
Расход жидкости составит
![]() (7.8)
(7.8)
Таким образом, имеем те же расчетные формулы, что и при свободном истечении, только расчетный напор Нр в данном случае представляет собой разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход не зависят от высоты расположения отверстия.
Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в атмосферу.
Применяя тот же метод, который был использован для вывода уравнения (7.2), и используя уравнение Бернулли для сжимаемого вязкого газа (5.10), можно получить формулу для определения скорости истечения газа из отверстия:
 (7.9)
(7.9)
где н - начальная (в сечении 1-1) плотность газа,
Расход газа через
отверстие составит:
![]()
или с учетом (7.9) будет
 .
(7.10)
.
(7.10)
7.2. Истечение через насадки при постоянном напоре
Насадками называются присоединенные к отверстию в стенке резервуара или трубе короткие трубки определенной длины, в которых имеется напорное движение. Для определения скорости истечения и расхода жидкости через насадки применяют те же формулы, что и для малого отверстия в тонкой стенке, но коэффициенты , , в них имеют другие значения в зависимости от формы насадки. Основные типы насадков приведены на рис. 7.3.
Внешним цилиндрическим насадком (насадком Вентури) называется прямая цилиндрическая трубка длиной l = (3 - 4)d, присоединенная под прямым углом с внешней стороны резервуара к отверстию того же диаметра (рис.7.3,а).
При входе в такую короткую трубку кривизна линий тока (траекторий) значительна, благодаря чему во входной части трубки происходит сжатие потока подобное тому, что и при истечении через отверстие. Затем поток расширяется, заполняя все сечение насадки. Вокруг сжатого сечения образуется кольцевая вихревая водоворотная зона, подобно той, что имеет место при внезапном сужении трубопровода.
Содержащиеся в жидкости газы и выделившиеся из жидкости пары, зажатые в водоворотной зоне, довольно быстро уносятся транзитным потоком. В вихревой зоне понижается давление.
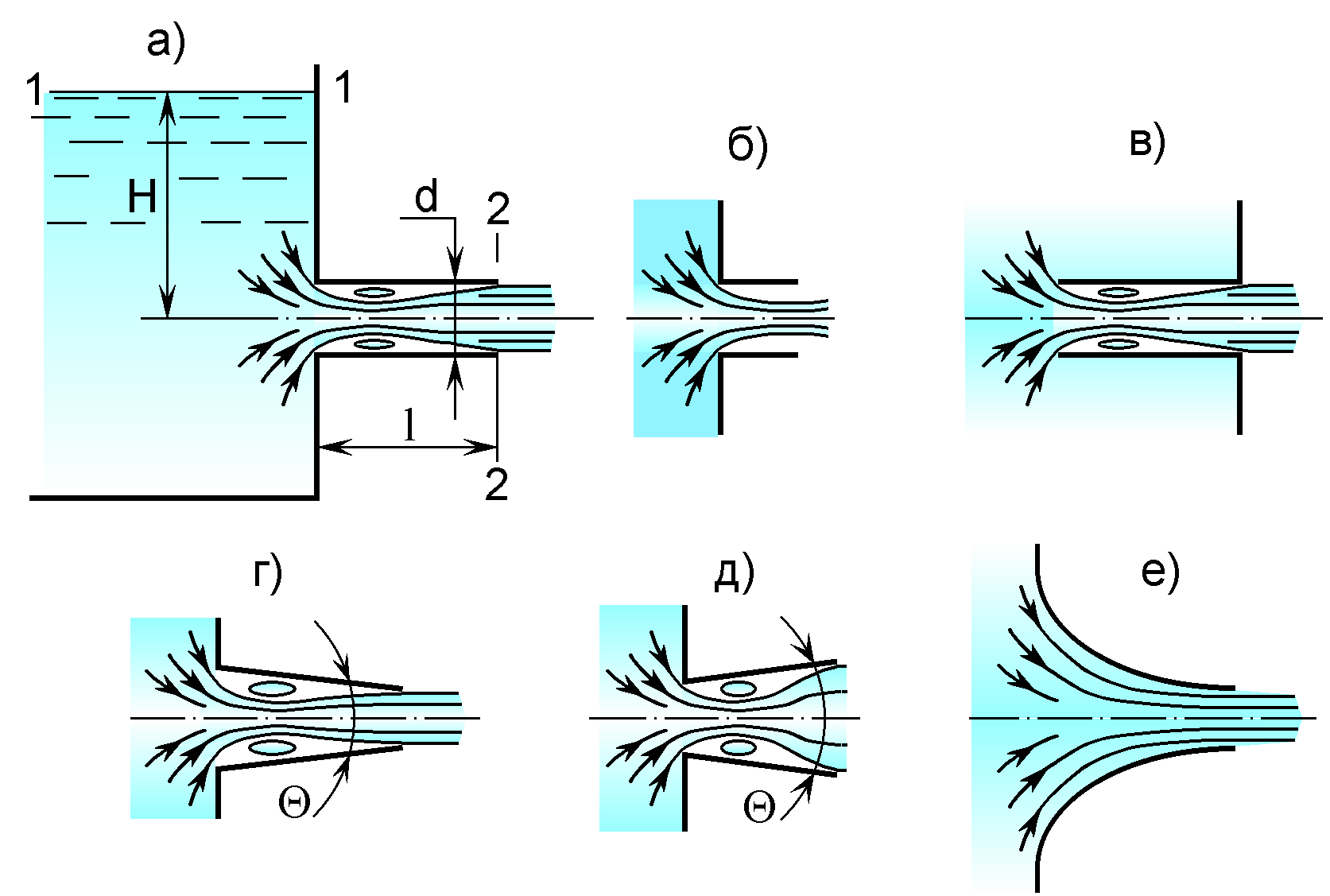
Рис. 7.3. Типы насадков
В связи с наличием вакуума в сжатом сечении действующий напор увеличивается на величину этого вакуума. Скорость в сжатом сечении увеличивается по сравнению с истечением через отверстие с острой кромкой. Насадок как бы "подсасывает" жидкость.
В то же время в насадке происходят и дополнительные по сравнению с отверстием с острой кромкой потери напора, связанные с внезапным расширением струи за сжатым сечением. Соотношение влияния "подсасывания" и указанных дополнительных потерь напора на пропускную способность и определяет степень изменения расхода через насадок по сравнению с отверстием.
Запишем уравнение Бернулли для участив между сечениями 1-1 и 2-2 (рис. 7.3,а).
Считая на выходе
из насадка коэффициент Кориолиса
=1 и пренебрегая
скоростным напором в сечении 1-1 ( 1V1/2g
= 0),получим при
p1
= p2:
![]() ,
,
где V - скорость в выходном сечении насадка (в сечении 2-2).
В рассматриваемом случае сопротивление движению жидкости состоит из сопротивлений при сужении, аналогичных сопротивлениям в отверстии в тонкой стенке, и сопротивлений при внезапном расширении струи от площади сжатого сечения Sc до площади на выходе из насадка S, т.е.
![]() .
.
Для расчетов удобнее все коэффициенты сопротивлений отнести к скорости V в выходном сечении насадка.
Определим численные значения коэффициентов сопротивлений при достаточно больших значениях числа Re, когда коэффициент сжатия струи не зависит от числа Re.
Коэффициент сопротивления при истечении через отверстие с острой кромкой, отнесенный к скорости в сжатом сечении Vc, равен o = 0,06.
С учетом =
SC/S
= 0,61 - 0,64 получим![]()
При внезапном
расширении струи в насадке от Sc
до S,
приняв
![]() получим
получим
![]()
Коэффициент сопротивления при входе в насадок равен сумме коэффициентов сопротивлений на сужение и на расширение струи внутри насадка, равной при средних значениях соответствующих коэффициентов сопротивлений
![]() .
.
Тогда
![]() ,
(7.11)
,
(7.11)
где
![]() .
.
Коэффициент расхода для насадка равен ц.н. = ц.н., так как =1, поскольку сжатия потока на выходе из насадка нет.
Опыты показали, что максимальные значения коэффициента расхода соответствуют длине насадка
1опт = (3 - 4)d, когда потери напора по длине малы и ими можно пренебречь.
При длине насадка 1н < 1опт (рис. 7.3,6) струя отжимается наружным давлением от стенок насадка, и истечение жидкости происходит аналогично истечению через отверстие. При 1н > 1опт к действующим сопротивлениям добавляются сопротивления на трение по длине, т.е.
![]() ,
,
где - коэффициент Дарси.
При некоторой относительной длине насадка 1/d коэффициент расхода при истечении через него равен коэффициенту расхода при истечении через отверстие с острой кромкой o . Эта длина составит
![]() .
(7.12)
.
(7.12)
При o = 0,6 и = 0,05 будет 1/d = 25.
Кроме цилиндрических наружных насадков в технике применяются цилиндрические внутренние насадки (рис.7.3,в) и насадки другой формы.
На рис.7.3,г показан конический сходящийся насадок, используемый в том случае, когда при данном полном напоре нужно максимально увеличить кинетическую энергию струи ради увеличения дальности полета струи и силы ее удара. Увеличение угла конусности приводит к уменьшению потерь на расширение струи после сжатия в пределах насадка. При углах конусности 13-14° эти потери практически ничтожны, т.к. в этом случае практически Sc = S.
Конический расходящийся насадок (рис.7,3,д) используют для преобразования части кинетической энергии потока в потенциальную, когда нужно уменьшить скорость выхода жидкости или увеличить давление (например, в выходных элементах насосов и вентиляторов).
Наиболее совершенным является коноидальный насадок (рис.7.3,е). Его форма соответствует форме вытекающей через отверстие струи. За счет этого сжатие струи на выходе из такого насадка отсутствует, т.е. = 1. Ниже в табл. 7.1 приведены для сравнения характеристики рассмотренных типов насадков.
Таблица 7.1.
Тип насадка или отверстия |
Рисунок |
|
|
|
Круглое отверстие в тонкой стенке |
7.1 |
0,98 |
0,64 |
0,62 |
Цилиндрический внешний насадок |
7.3,а |
0,82 |
1 |
0,82 |
Цилиндрический внутренний насадок |
7.3,в |
0,71 |
1 |
0,71 |
Конический сходящийся насадок ( = 13,4°) |
7.3,г |
0,984 |
0,98 |
0,946 |
Конический расходящийся насадок ( = 7°) |
7.3,д |
0,45 |
1 |
0,45 |
Коноидальный насадок |
7.3,е |
0,98 |
1 |
0,98 |
