Гидравлика (курс лекций) введение

Гидравлика – это прикладная наука, изучающая законы равновесия и движения жидкостей.

Областью применеия теоретических знаний, изучаемых в курсе гидравлики, является гидроэнергетика (использование энергии водных ресурсов), водоснабжение и канализация, мелиорация (осушение или орошение), гидропривод, судоплавание.

Гидравлику подразделяют на гидростатику и гидродинамику.

Гидростатика изучает законы равновесия жидкостей, а гидродинамика – законы движения жидкости.

Основоположником гидравлики считается Архимед (250 г. до н. э.), который занимался вопросами гидростатики и плавания.

Знаменитые открытия и изобретения, такие как центробежный насос, парашют, анемометр были сделаны еще в эпоху Возрождения знаменитым художником и инженером Леонардо да Винчи.

Большой вклад в становлении гидравлики как науки сделаны Галилеем, Торричелли, Паскалем, Бернулли, Эйлером, Рейнольдсом, Прантлем, Колмогоровым и др.

ЛЕКЦИЯ 1. ЖИДКОСТИ И ИХ ФИЗИЧЕСКИЕ СВОЙСТВА. МОДЕЛИ ЖИДКОСТИ. СИЛЫ, ДЕЙСТВУЮЩИЕ В ЖИДКОСТИ.

1.1 Жидкости и их физические свойства

Жидкость  агрегатное состояние вещества, сочетающее в себе как свойства твердого тела (постоянство объема), так и газообразного состояния (изменчивость формы). Под общим названием жидкости объединяют капельные жидкости (вода, спирт, керосин и др.) и газы (воздух, метан и др.).

Плотностью называется физическая величина, численно равная отношению массы тела к его объему:

, (1.1)

где m – масса жидкости, кг; V – объем сосуда, который занимает жидкость, м³ .

Удельный вес – вес единицы объема жидкости:

, (1.2)

Сжимаемостью называется свойство жидкости изменять свой объем при изменении давления и температуры.

Сжимаемость характеризуется коэффициентом объемного сжатия β_V, которое определяет относительное уменьшение объема жидкости при увеличении давления:

, (1.3)

где V₀ – начальный объем, м³ ; dV – элементарное изменение объема, м³; dp –элементарное изменение давления, Па.

Температурное расширение жидкостей характеризуется коэффициентом температурного расширения β_T, определяющим увеличение объема жидкости при повышении температуры:

, (1.4)

где dT – элементарное изменение температуры, К.

Теплопроводность представляет собой физическую величину, определяющую способность тел проводить тепло. Теплопроводность зависит от природы вещества, его структуры, температуры и других факторов. Теплопроводность жидкостей меняется в диапазоне от 0,06 до 0,7 .

С увеличением температуры теплопроводность у всех жидкостей, за исключением воды и глицерина, уменьшается.

Согласно молекулярно-кинетической теории теплопроводность определяется формулой

, (1.5)

где λ – коэффициент теплопроводности, ; – средняя скорость перемещения молекул, м/c; – средняя длина свободного пробега молекул, м; c_v – удельная (массовая) изохорная теплоемкость газа ; ρ – плотность.

Более точные результаты зависимости теплопроводности от температуры дает интерполяционная формула

, (1.6)

где λ₀ – теплопроводность при T = 273К .

Вязкость  это свойство жидкости (газа) оказывать сопротивление относительному сдвигу ее слоев. Это свойство проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения, или силами вязкости.

Механизм возникновения силы вязкости можно представить из опыта (рис.1.3).

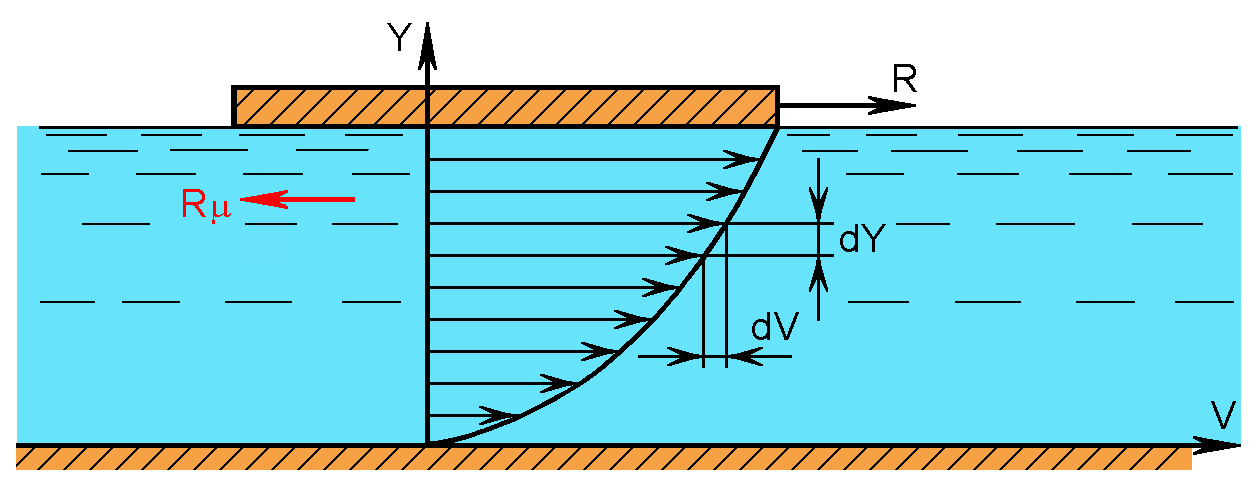
Рис.1.3. Схема для определения силы вязкости

На свободной поверхности неподвижного объема жидкости находится легкая пластинка площадью S. Для ее смещения потребуется приложить силу R. Это значит, что жидкость оказывает сопротивление, т.е. возникает сила вязкости R_µ= -R.

Она обусловлена тем, что слой жидкости, прилегающий к пластине, прилипает к ней и движется вместе с пластиной с ее скоростью.

Ввиду наличия молекулярного взаимодействия этот слой увлекает за собой следующий слой и т.д. Вместе с тем, нижний слой жидкости, непосредственно примыкающий к неподвижному дну, будет иметь нулевую скорость.

Таким образом, в жидкости возникает слоистое движение с некоторым распределением скоростей по высоте . Между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений.

Согласно гипотезе, высказанной впервые Ньютоном в 1686 г., а за­тем экспериментально обоснованной проф. Н.П. Петровым в 1883 г., касательные напряжения в жидкости зависят от ее рода и характера тече­ния, и при слоистом течении изменяются прямо пропорционально попе­речному градиенту скорости

, (1.7)

где µ  коэффициент пропорциональности, получивший название динамического коэффициента вязкости; dV  приращение скорости при приращении координаты dу (рис.1.3).

Закон Ньютона применим только к слоистым потокам. Знак плюс или минус выбирается так, чтобы значение µ было положительным независимо от выбора положительного направления у.

Из формулы (1.7) следует, что касательные напряжения возможны только в движущейся жидкости, т.е. вязкость жидкости проявляется лишь при ее течении.

Жидкости, для которых справедлив закон внутреннего трения Ньютона, называются ньютоновскими.

Существуют жидкости (коллоидные суспензии, растворы полимеров, гидросмеси из глины, мела, цемента, сапропелей, илов, бетонные гидросмеси, кормовые смеси и т.п.), для которых связь между касательным напряжением  и скоростью сдвиговой деформации dV/dy выражается иными соотношениями. Такие жидкости называются неньютоновскими.

При сотношении

, (1.8)

жидкости называются вязкопдастичными и их движение начинается лишь после того, как внешней силой будет преодолено начальное напряжение сдвига ₀.

Для других неньютоновских жидкостей динамическая вязкость мо­жет зависеть от градиента скорости, времени и т.д.

При постоянстве касательных напряжений по поверхности S полная касательная сила (сила вязкости) по этой поверхности составит

. (1.9)

Динамический коэффициент вязкости µ, являющийся основной конечной характеристикой вязкости жидкостей и газов, имеет размерность Па с. Коэффициент динамической вязкости имеет и физический смысл

. (1.10)

Таким образом, динамический коэффициент вязкости есть работа, которую необходимо совершить на относительное сдвижение слоев жидкости для единицы объемного расхода жидкости через рассматриваемое сечение потока жидкости.

Наряду с динамическим коэффициентом вязкости используется кинематический коэффициент вязкости, определяемый соотношением

. (1.11)

Размерность коэффициента кинематической вязкости в системе СИ  м²/с, а в технической системе см²/с = Стокc.

Физический смысл кинематического коэффициента вязкости представляется как работа, которую необходимо совершить на относительное сдвижение слоев жидкости для единицы массового расхода жид­кости через рассматриваемое сечение потока жидкости.

Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис.1.4). Вязкость газов, наоборот, с увеличением температуры возрастает.

Объясняется это различием природы вязкости в жидкостях и газах. В жидкости молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает.

Испаряемость  свойство жидкости переходить в пар. Обратный переход пара в жидкость называется конденсацией. Если жидкость дос­таточно длительное время находится в закрытом сосуде, то наступает равновесие, когда число молекул, перешедших из жидкости в пар, равно числу молекул, совершивших обратный переход. В этом случае пар называется насыщенным, и в нем устанавливается определенное для данной температуры давление. Такое давление называется упругостью насыщенного пара.

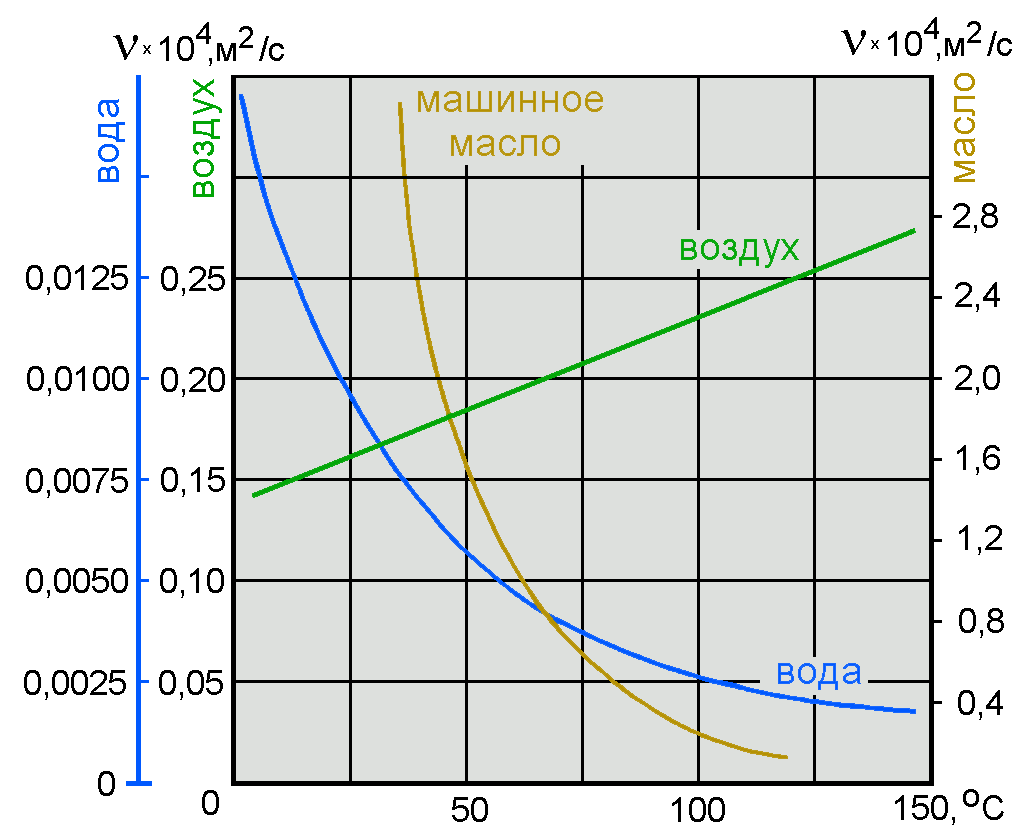
Рис.1.4. Зависимость кинематического коэффициента вязкости воды, воздуха и машинного масла от температуры

Образование насыщенных паров приводит к тому, что на свободной поверхности жидкости не может быть достигнуто давление ниже упругости насыщенного пара, соответствующей данной температуре.

Испарение жидкости может происходить не только со свободной поверхности, а и внутрь пузырей, образующихся в ней при определенной температуре и давлении. Такой фазовый переход называется кипением. Он может наступить в покоящейся или движущейся жидкости при давлении, равном упругости насыщенного пара при данной температуре, или при температуре, равной температуре кипения при данном давлении.

Установлено, что кипение возникает только в том случае, когда в жидкости имеются пузырьки защемленного у стенок газа или если такие пузырьки образуются вследствие выделения газа, растворенного в жид­кости. Если температура жидкости повышается или давление в ней падает, то пузырьки растут в объеме и прорываются наружу через свободную поверхность. Наблюдается процесс кипения.

Дегазированные жидкости не кипят при температуре, значительно превышающей температуру кипения, и при давлении ниже упругости насыщенного пара.

Кипение жидкости приводит к нарушению сплошности среды. В гидромеханике особенно важен случай кипения, который возникает в движущейся жидкости вследствие местных понижений давления до упругости насыщенного пара (р_пар). Такой вид кипения называется кавитацией (от латинского cavitas  пустота). Снижение давления в потоке жидкости происходит из-за возникновения на отдельных его участках больших местных скоростей. (рис.1.4).

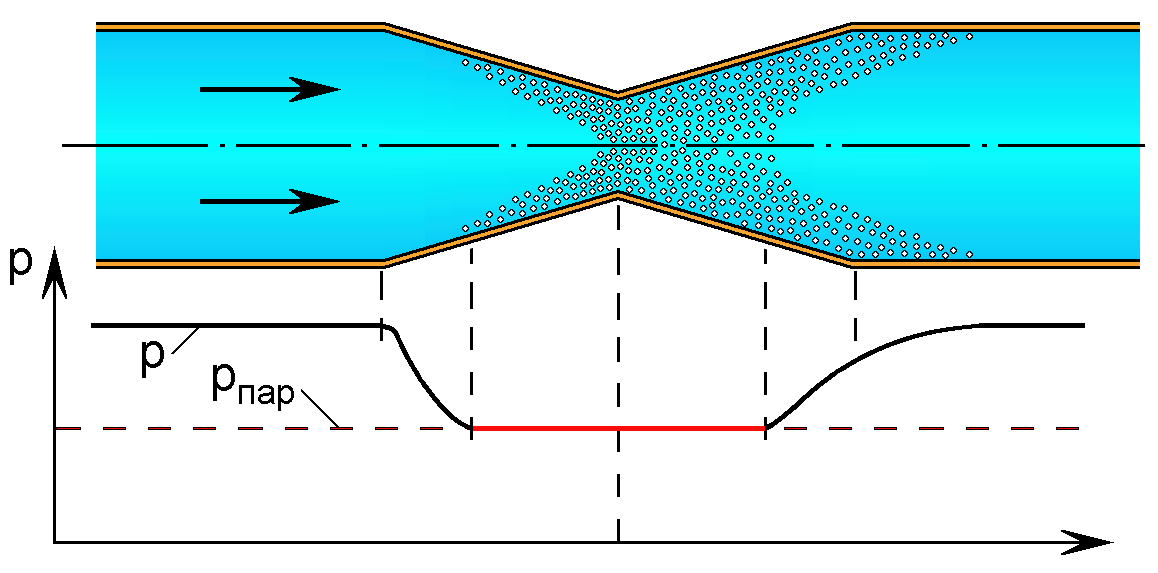
Рис.1.4. Кавитационная зона в трубе с местным сужением

В узком месте трубы диаметр трубы уменьшился в 3 раза, а скорость потока возросла в 9 раз, что привело к снижению давления и при p = p_пар образуется кавитационная зона, состоящая из парогазовых пузырьков.

Пузырьки перемещаются потоком жидкости в направлении его движения. Там, где давление продолжает снижаться, пузырьки растут в объеме и сливаются (соединяются) в большие пузыри-каверны.

Таким образом, нарушается сплошность потока и его физические характеристики (плотность, сжимаемость и др.)

В расширяющейся части трубы давление снова возрастает и парогазовые пузырьки начинают сокращаться в размерах (cхлапываться) до полной конденсации пара в жидкость. Процесс схлапывания сопровождается местными повышениями давления (своего рода гидроудар).

Если это происходит вблизи стенок, то возникает усталостное разрушение материала этих стенок (так называемая эрозия).

Явление кавитации особенно опасно проявляется на лопастях винтов морских судов, крыльчатках вентиляторов и в центробежных насосах.