3.2. Доказательство критерия управляемости Калмана

Соотношения 389 представляют собой систему неоднородных алгебраических уравнений с постоянными коэффициентами. Вектор неизвестных компонент обобщенного управления 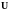в этой системе состоит из интегралов

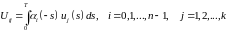, 90390\* MERGEFORMAT (.)

где 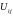и 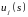j-ые элементы вектора , определенного 384, и вектора управления . Вектор z в правой части системы 389 постоянен и определён формулой 378.

Таким образом, для определения nk неизвестных имеем n неоднородных уравнений. Условие существования решения неоднородной системы линейных алгебраических уравнений даёт следующая теорема.

ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛИ:

Система неоднородных уравнений имеет решение тогда и только тогда, ранг расширенной матрицы системы равен рангу самой системы.

Расширенная матрица системы состоит из матрицы коэффициентов линейной системы (в нашем случае W) и столбца свободных членов (у нас z).

Таким образом, условие существования решения 389 есть

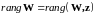_. 91391\* MERGEFORMAT (.)

Напомним, что

Определение

Ранг матрицы равен наибольшему порядку ненулевого минора матрицы. Другое, эквивалентное определение ранга матрицы: ранг матрицы равен числу линейно независимых столбцов (или строк) матрицы.

В силу произвольности столбца свободных членов z, условие 391 имеет вид

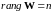92392\* MERGEFORMAT (.)

Оглавление

В самом деле, если предположить, что ранг матрицы W меньше n, тогда множество линейно независимых столбцов W составляет неполный базис n-мерного пространства. Добавление к этому множеству произвольного столбца z (в частности ортогонального к множеству столбцов W) на единицу увеличит количество линейно независимых столбцов. В случае если ранг матрицы W равен n, (а это максимально возможное значение ранга W, так как в матрице W ровно n строк), то дополнительный столбец не может увеличить ранг.

Итак, при выполнении условия 392 компоненты вектора обобщенного управления могут быть определены и, возможно, неоднозначно. Остается открытым вопрос о разрешимости соотношений 390, связывающих и .

Попытаемся найти в виде разложения по линейно независимым функциям , то есть

93393\* MERGEFORMAT (.)

Подставляя выражение 393 в 384, получим

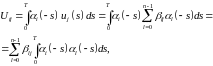94394\* MERGEFORMAT (.)

Введем матрицу G, состоящую из элементов

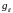
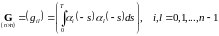95395\* MERGEFORMAT (.)

такая матрица носит название матрицы Грама. Она симметрична и обратима. Последнее выполняется потому, что коэффициенты 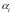разложения матричной экспоненты по степеням матрицы А являются линейно независимыми функциями.

С учётом введённых обозначений соотношение 394 примет вид

Оглавление

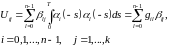. 96396\* MERGEFORMAT (.)

_{Сформируем из компонент} вектора обобщённого управления (их всего nk) k векторов 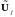размерности

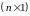
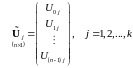97397\* MERGEFORMAT (.)

а из коэффициентов 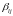(их всего также nk) k векторов 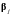той же размерности

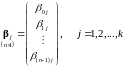98398\* MERGEFORMAT (.)

Тогда вместо nk скалярных уравнений 396 для 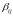могут быть записаны k матричных, для n- мерных векторов

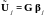99399\* MERGEFORMAT (.)

В силу обратимости матрицы Грама G, матричные уравнения разрешимы относительно векторов .

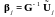1003100\* MERGEFORMAT (.)

А значит, коэффициенты разложения 393 координат 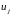вектора управления по функциям могут быть найдены. На этом доказательство теоремы Калмана о критерии управляемости систем с векторным управлением завершается.

Оглавление