Лекция 2. Линейные динамические системы

Решение однородных и неоднородных систем линейных дифференциальных уравнений. Весовая матрица, теорема Коши, теорема Гамильтона-Кэли, матричная экспонента

2.1. .Весовая матрица. Решение систем линейных дифференциальных уравнений. Теорема Коши

Рассмотрим динамическую систему, поведение которой описывается системой линейных дифференциальных уравнений с постоянными коэффициентами

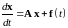, 31231\* MERGEFORMAT (.)

где

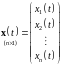- вектор переменных состояния, 32232\* MERGEFORMAT (.)

- постоянная матрица системы, 33233\* MERGEFORMAT (.)

34234\* MERGEFORMAT (.)

вектор в правой части системы уравнений 231, вообще говоря, непостоянный.

Для решения системы необходимо задать вектор переменных состояния в начальный момент времени .

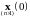Оглавление

Если вектор 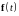тождественно равен нулю, то система уравнений 231 называется однородной и имеет вид

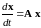35235\* MERGEFORMAT (.)

Определение

Характеристическим уравнением матрицы А называется

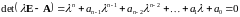_. 36236\* MERGEFORMAT (.)

Определение

Весовой матрицей линейной системы уравнений 231 или 235 называется матрица

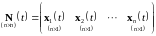, 37237\* MERGEFORMAT (.)

составленная из n частных решений 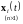однородной системы уравнений 235, удовлетворяющих начальным условиям

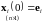, 38238\* MERGEFORMAT (.)

где - единичные вектора

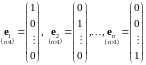. 39239\* MERGEFORMAT (.)

Так как весовая матрица 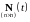состоит из столбцов, представляющих собой частные решения однородной системы уравнений 235 с единичными начальными условиями 238, то и весовая матрица удовлетворяет 237 и единичным начальным условиям

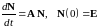. 40240\* MERGEFORMAT (.)

В 240 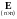- n мерная единичная матрица

Оглавление

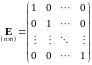. 41241\* MERGEFORMAT (.)

Общее решение однородной системы дифференциальных уравнений 235 имеет вид

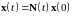, 42242\* MERGEFORMAT (.)

где

43243\* MERGEFORMAT (.)

вектор начальных условий для вектора переменных состояния 232.

Общее решение неоднородной системы 231 равно сумме общего решения 242 однородной системы 235 и частного неоднородной 231 с нулевыми начальными условиями.

Теорема Коши

Частное решение неоднородной системы уравнений (1.1) с нулевыми начальными условиями может быть записано в виде интеграла свертки

44244\* MERGEFORMAT (.)

Докажем теорему Коши.

Интеграл 244 равен 0, при 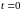. Это очевидно. Значит, решение 244 удовлетворяет нулевым начальным условиям.

Производная от интеграла свертки 244 равна

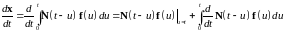45245\* MERGEFORMAT (.)

При преобразовании первого слагаемого примем во внимание, что весовая матрица 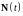удовлетворяет единичным начальным условиям

. 46246\* MERGEFORMAT (.)

Оглавление

При преобразовании второго, что весовая матрица удовлетворяет однородному уравнению

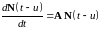, 47247\* MERGEFORMAT (.)

а постоянная матрица А может быть вынесена из-под знака интеграла, то есть

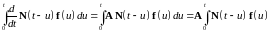. 48248\* MERGEFORMAT (.)

Интеграл в 248 не что иное, как интеграл свертки , значит для него справедливо

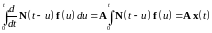. 49249\* MERGEFORMAT (.)

Тогда из 245, 246 , 248 следует

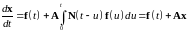. 50250\* MERGEFORMAT (.)

Теорема Коши доказана.

2.2. Матричная экспонента. Теорема Гамильтона-Кэли

Определение

Экспонентой от матрицы А называется бесконечный ряд

51251\* MERGEFORMAT (.)

Экспонента от матрицы быть определена только для квадратной матрицы и представляет собой квадратную матрицу таких же размеров, как и матрица А.

Утверждение

Экспонента от матрицы 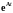равна весовой матрице .

В самом деле, при , матричная экспонента 251 равна единичной матрице 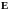241, так же, как и весовая матрица.

Производная в силу её определения 251 равна

Оглавление

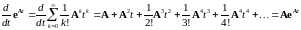, 52252\* MERGEFORMAT (.)

то есть, удовлетворяет однородной системе уравнений 235, той же, что и весовая матрица .

Таким образом, утверждение доказано, и задача определения весовой матрицы оказалась тождественной задаче определения матричной экспоненты.

Для нахождения матричной экспоненты применим следующую теорему.

Теорема Гамильтона-Кэли

Всякая матрица удовлетворяет своему характеристическому уравнению. То есть

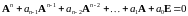_. 53253\* MERGEFORMAT (.)

Из теоремы Гамильтона –Кэли следует, что все степени матрицы А порядка большего, чем n-1, могут быть выражены через степени матрицы А порядка меньшего, чем n. В самом деле, для n-ой степени матрицы А из 253 имеем

_. 54254\* MERGEFORMAT (.)

Тогда для матрицы 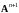_{получим}

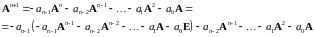55255\* MERGEFORMAT (.)

И так далее. Если провести эту процедуру для всех слагаемых бесконечного ряда 252, то окажется, что матричная функция представлена в виде разложения по степеням матрицы А до порядка n-1 включительно с коэффициентами, зависящими от времени

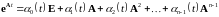_. 56256\* MERGEFORMAT (.)

Вычислим производную по времени от матричной экспоненты в соответствии с представлением её 256

57257\* MERGEFORMAT (.)

Оглавление

Поскольку матричная экспонента удовлетворяет дифференциальному уравнению

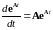, 58258\* MERGEFORMAT (.)

то из 256 следует

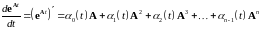59259\* MERGEFORMAT (.)

Применяя теорему Гамильтона-Кэли 253 для понижения степени матрицы А в 259 , получим

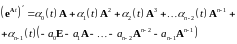, 60260\* MERGEFORMAT (.)

или

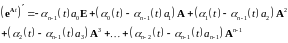61261\* MERGEFORMAT (.)

Приравнивания коэффициенты при одинаковых степенях матрицы А, получим систему дифференциальных уравнений для функций

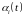
. 62262\* MERGEFORMAT (.)

_{В соответствии с представлением} 256_{, начальные условия для коэффициентов будут}

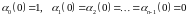_. 63263\* MERGEFORMAT (.)

Система уравнений 262 с начальными условиями 263 может быть записана в матричной форме

Оглавление

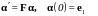_, 64264\* MERGEFORMAT (.)

где

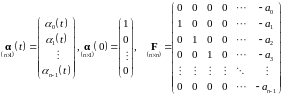. 65265\* MERGEFORMAT (.)

Тогда из 264, 265 для начальных условий получим

_, 66266\* MERGEFORMAT (.)

и, как следствие, из 263, 266

_. 67267\* MERGEFORMAT (.)

В 266, 267 верхний индекс в скобках обозначает порядок производной по времени.

Замечание 1:

Структура системы уравнений 262 такова, что она всегда может быть сведена к одному уравнению для коэффициента

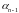
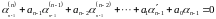_. 68268\* MERGEFORMAT (.)

Начальные условия для коэффициента и его производных в соответствии с 267 равны

_. 69269\* MERGEFORMAT (.)

То есть, функция 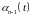есть весовая функция дифференциального уравнения, характеристическое уравнение которого совпадает с характеристическим уравнением матрицы А.

Замечание 2:

Функции где, 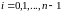, линейно независимы.

Оглавление

В самом деле, составим линейную комбинацию и приравняем ее нулю

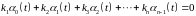_. 70270\* MERGEFORMAT (.)

Как следует из 263, равенство 270, при выполняется, только если 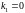. Производная выражения 270 равна

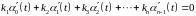_. 71271\* MERGEFORMAT (.)

Согласно 267 равенство 271 при выполняется, только если .

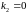Выполняя дифференцирование до порядка n-1 включительно, получим, что, в силу начальных условий 267 и остальные коэффициенты 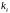равны 0. Таким образом, линейная комбинация функций может быть равна нулю только при нулевых коэффициентах, что и доказывает линейную независимость .