Оглавление

ЛЕКЦИЯ 1. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТРЕЛЫ МОСТОВОГО КРАНА 3

1.1. Постановка задачи. Описание модели 3

1.2. Уравнения движения 3

1.3. Уравнения малых колебаний 7

1.4. Нормализация. Переход к безразмерным переменным 8

1.5. Решение уравнений вынужденных колебаний 10

1.5.1. Случай резонанса 13

1.5.2. Нерезонансный случай 14

1.5.3. Биения 17

1.6. Вопросы для самоконтроля 18

ЛЕКЦИЯ 2. ЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ 20

2.1. .Весовая матрица. Решение систем линейных дифференциальных уравнений. Теорема Коши 20

2.2. Матричная экспонента. Теорема Гамильтона-Кэли 25

2.3. Пример решения линейной системы дифференциальных уравнений 30

2.4. Вопросы для самоконтроля 34

ЛЕКЦИЯ 3. УПРАВЛЯЕМЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ. КРИТЕРИЙ УПРАВЛЯЕМОСТИ КАЛМАНА 36

3.1. Представление решения линейной управляемой системы с помощью матричной экспоненты. Матрица управляемости Калмана 36

3.2. Доказательство критерия управляемости Калмана 42

3.3. Критерий управляемости Калмана для систем со скалярным управлением 47

3.3. Вопросы для самоконтроля 48

ЛЕКЦИЯ 4. УПРАВЛЯЕМЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ. КРИТЕРИЙ УПРАВЛЯЕМОСТИ ХАУТУСА 49

4.1. Критерий управляемости Хаутуса 49

4.2. Критерий управляемости для линейных систем второго порядка 51

4.3. Вопросы для самоконтроля 55

ЛЕКЦИЯ 5. ЗАДАЧА ОДНОВРЕМЕННОГО УПРАВЛЕНИЯ ДВУМЯ МАЯТНИКАМИ 56

5.1. Уравнения движения системы двух маятников 56

5.2. Анализ управляемости системы по критерию Калмана 59

5.3. Анализ управляемости системы по критерию Хаутуса 62

ЛЕКЦИЯ 6. СИНТЕЗ УПРАВЛЕНИЯ В ЗАДАЧЕ О СТАБИЛИЗАЦИИ МАЯТНИКА В ВЕРХНЕМ ПОЛОЖЕНИИ РАВНОВЕСИЯ 64

6.1. Фазовая плоскость. Типы особых точек линейного дифференциального уравнения второго порядка 64

6.1.1. Центр 66

6.1.2. Устойчивый фокус 68

6.1.3. Неустойчивый фокус 70

6.1.4. Седло 72

6.1.5. Устойчивый узел 73

6.2 Задача управления колебаниями маятника около верхнего положения равновесия. Синтез управления при наличии ограничения на управление. Построение области управляемости 75

6.3. Синтез управления при наличии ограничения на управление. Метод выделения неустойчивой координаты 84

6.4. Вопросы для самоконтроля 89

11Equation Section (Next)

Оглавление

Л екция 1. Вынужденные колебания стрелы мостового крана

Уравнения малых колебаний, линеаризация, нормализация, вынужденные колебания, теорема Коши, резонанс, биения

1.1. Постановка задачи. Описание модели

Модель мостового крана (рис. 1) состоит из двух тел: тележки, перемещающейся по горизонтальным направляющим и точечного груза, связанного с тележкой невесомым нерастяжимым тросом. Масса тележки 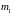, масса груза 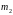, длина троса . Трение между тележкой и направляющими отсутствует. На тележку действует периодическая сила 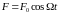, где 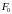- амплитуда, частота возмущающей силы.

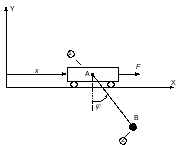
Рис.1 Модель мостового крана

1.2. Уравнения движения

Рассматриваемая модель представляет собой механическую систему с двумя степенями свободы и идеальными голономными связями. В качестве обобщенных координат выберем координату , задающую положение тележки, и угол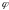 отклонения троса от вертикали. Уравнения движения системы составим в форме уравнений Лагранжа второго рода.

Согласно общей методике, запишем кинетическую энергию системы

Оглавление

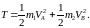212\* MERGEFORMAT (.)

Проекции скоростей точек A и B на оси координат равны

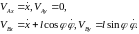313\* MERGEFORMAT (.)

Здесь и далее точкой обозначается дифференцирование по времени t.

Кинетическая энергия системы 12

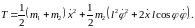414\* MERGEFORMAT (.)

Потенциальная энергия

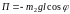515\* MERGEFORMAT (.)

Функция Лагранжа

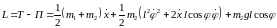616\* MERGEFORMAT (.)

Для определения обобщенных неконсервативных сил, обусловленных наличием периодической силы, действующей на тележку, найдём элементарную работу этой силы на возможном перемещении точки приложения силы

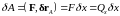. 717\* MERGEFORMAT (.)

Следовательно, обобщенные неконсервативные силы равны

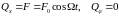. 818\* MERGEFORMAT (.)

Вычисляя необходимые для составления уравнений Лагранжа производные, получим

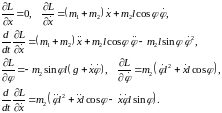919\* MERGEFORMAT (.)

Тогда уравнения Лагранжа будут

Оглавление

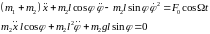10110\* MERGEFORMAT (.)

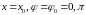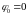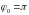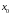При отсутствии возмущающей силы уравнения 110 допускают частные решения . Эти решения соответствуют положениям равновесия системы, в которых тележка покоится, а груз занимает либо нижнее, , либо верхнее, положение равновесия. Значение координаты в положении равновесия, вообще говоря, не определено.