6.1.4. Седло

Если характеристическое уравнение имеет два действительных корня различных знаков, то есть, , особая точка называется седло.

Это выполняется, если

, 1836183\* MERGEFORMAT (.)

величина коэффициента 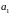значения не имеет. В частном случае, когда

1846184\* MERGEFORMAT (.)

корни характеристического уравнения равны

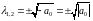. 1856185\* MERGEFORMAT (.)

Интегрирование уравнений фазовых траекторий 6170 при условии 6184 определяет семейство гипербол, симметричных относительно осей

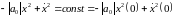1866186\* MERGEFORMAT (.)

Фазовые кривые для различных начальных условий приведены на рисунке 7. Цифрой 3 на рисунке обозначены прямые

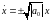, 1876187\* MERGEFORMAT (.)

представляющие частный случай фазовых траекторий, соответствующий нулевому значению константы в уравнениях 6186. Двигаясь по этим траекториям, изображающая точка может попасть в начало координат только за бесконечное время. Эти прямые разделяют характерные области движения.

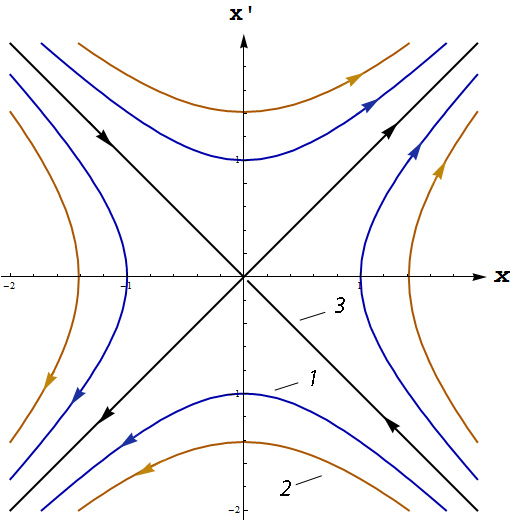
Рис. 7 Особая точка типа седло

Оглавление

Если коэффициенты характеристического уравнения

, 1886188\* MERGEFORMAT (.)

тоже будет седло, только фазовые траектории уже не будут симметричны относительно осей. Симметрия относительно центра сохранится. Решение уравнения 6164 для случая двух действительных корней характеристического уравнения имеет вид

, 1896189\* MERGEFORMAT (.)

и, в случае корней разных знаков, будет содержать возрастающую и убывающую экспоненты.

Седло является неустойчивой особой точкой.

6.1.5. Устойчивый узел

Если характеристическое уравнение имеет два действительных отрицательных корня, то имеет место устойчивый узел.

Для возникновения узла необходимо и достаточно, чтобы были выполнены условия

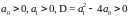1906190\* MERGEFORMAT (.)

Фазовый портрет устойчивого узла приведен на рисунке 8. Цифрами 3 и 4 на рисунке 8 обозначены фазовые траектории, уравнения которых имеют вид

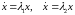, 1916191\* MERGEFORMAT (.)

Изображенная на рисунке 8 прямая 4 соответствует меньшему по модулю, (то есть большему по величине), корню характеристического уравнения. Все фазовые траектории, приближаясь к особой точке, касаются прямой 4.

Решение уравнения 6164 для случая двух действительных отрицательных корней характеристического уравнения имеет вид 6189, и содержит две убывающие экспоненты. Скорость убывания решения определяется величиной меньшего по модулю, (то есть большего по величине), отрицательного корня. Графики зависимости 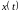, (соответствующие траекториям 1 и 2 на рисунке 8), приведены на рисунке 9.

Оглавление

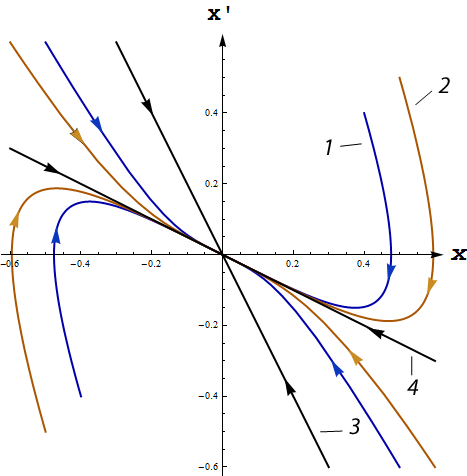
Рис. 8 Фазовый портрет устойчивого узла

Рис. 9 Зависимость в случае устойчивого узла

Устойчивый узел является асимптотически устойчивой особой точкой.

Замечание

Приведенный в лекции обзор типов особых точек не полный. Не упомянуты неустойчивый узел, вырожденные узлы.

Оглавление

6.2 Задача управления колебаниями маятника около верхнего положения равновесия. Синтез управления при наличии ограничения на управление. Построение области управляемости

Рассмотрим задачу об управлении колебаниями маятника. Модель маятника (рисунок 10) представляет собой твердое тело массы 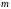, закрепленное в неподвижной точке О. Момент инерции тела относительно т.О равен . Расстояние от оси вращения до центра масс т.С обозначим 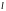. Положение маятника будем определять углом 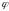между вертикалью и прямой ОС. Движение маятника происходит под действием сил тяжести и управляющего момента М. Модуль величины управляющего момента ограничен. Целью управления является стабилизация верхнего неустойчивого положения маятника.

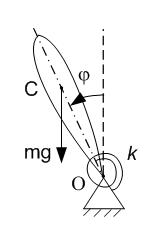
Рис. 10 Модель маятника

Уравнение движения маятника под действием сил тяжести и управляющего момента имеет вид

1926192\* MERGEFORMAT (.)

При малых углах отклонения, вместо уравнения 6192 будет

1936193\* MERGEFORMAT (.)

Переходя в уравнении 6193 к безразмерному времени в соответствии с формулами

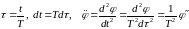, 1946194\* MERGEFORMAT (.)

получим

Оглавление

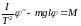, 1956195\* MERGEFORMAT (.)

или, разделив все члены уравнения 6195 на коэффициент при второй производной,

. 1966196\* MERGEFORMAT (.)

Выбирая в качестве нормализующего параметра значение

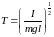, 1976197\* MERGEFORMAT (.)

получим уравнение

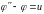1986198\* MERGEFORMAT (.)

Так как система со скалярным управлением, поведение которой описывается одним дифференциальным уравнением, согласно критерию Калмана, всегда управляема, то уравнение 6198 описывает управляемую систему.

Справа в уравнении 6198 стоит безразмерный управляющий параметр

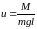. 1996199\* MERGEFORMAT (.)

Согласно заданному ограничению 6192 на величину действующего на маятник момента, управляющий параметр также ограничен

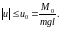2006200\* MERGEFORMAT (.)

Таким образом, нам предстоит найти закон управления в задаче с ограниченным управлением и заданными начальными и конечными условиями

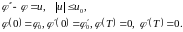2016201\* MERGEFORMAT (.)

Заметим, что при отсутствии управления, при 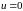, уравнение 6201 имеет вид

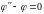. 2026202\* MERGEFORMAT (.)

Тривиальное решение уравнения 6202

2036203\* MERGEFORMAT (.)

Оглавление

определяет верхнее положение равновесия и является седлом, неустойчивой особой точкой (смотри п. 6.1.4.) Корни характеристического уравнения 6202 равны , фазовые траектории седла приведены на рисунке 7.

Задача синтеза управления, стабилизирующего неустойчивое состояние равновесия, состоит в нахождении закона изменения управляющего момента в виде обратной связи по параметрам состояния 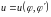. Ограничиваясь только линейной зависимостью, положим

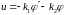2046204\* MERGEFORMAT (.)

Так как величина управляющего параметра 6200 ограничена, управление 6204 не может быть реализовано на всей плоскости 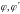, а только в той ее части, где 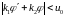. На плоскости эта область представляет собой полосу, ограниченную прямыми

. 2056205\* MERGEFORMAT (.)

Траектории внутри этой области удовлетворяют уравнению

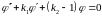2066206\* MERGEFORMAT (.)

положение равновесия будет асимптотически устойчивым, если

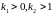, 2076207\* MERGEFORMAT (.)

и представлять собой устойчивый фокус, (см. п. 6.1.2), если

2086208\* MERGEFORMAT (.)

или устойчивый узел (см. п. 6.1.5), если

. 2096209\* MERGEFORMAT (.)

Таким образом, внутри области, где реализуется управление в виде обратной связи 6204 по параметрам состояния, при соответствующем подборе коэффициентов фазовые траектории “притягиваются” особой точкой.

Определение

Областью притяжения называется область, в которой фазовые траектории асимптотически стремятся к положению равновесия.

Положение области притяжения на фазовой плоскости зависит от коэффициентов и .

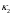На рисунке 11 для значений 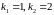, построены фазовые траектории 6208 и показана область (она обозначена буквой В), в которой

Оглавление

может быть реализовано управление 6204. Область В соответствует данному определению области притяжения. Цифрами 1 и 2 на рисунке обозначены ее 6205 границы.

Рис. 11 Фазовые траектории в области притяжения ( )

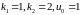При заданных значениях параметров начало координат представляет собой устойчивый фокус. Видно, что траектории не лежат целиком в области В, а выходят на границу. При попадании траектории на прямую 1 управление принимает значение , а на прямой 2 управление .

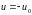При попадании траектории на границу 2 области С и в дальнейшем уравнение 6201 принимает вид

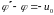. 2106210\* MERGEFORMAT (.)

Соответствующие фазовые траектории (рисунок 12 область С) представляют семейство гипербол с центром в точке и асимптотами

. 2116211\* MERGEFORMAT (.)

При выходе траекторий в область А уравнение движения 6201 становится

. 2126212\* MERGEFORMAT (.)

А фазовые траектории (рисунок 12) образуют семейство гипербол с центром в точке и асимптотами

2136213\* MERGEFORMAT (.)

Оглавление

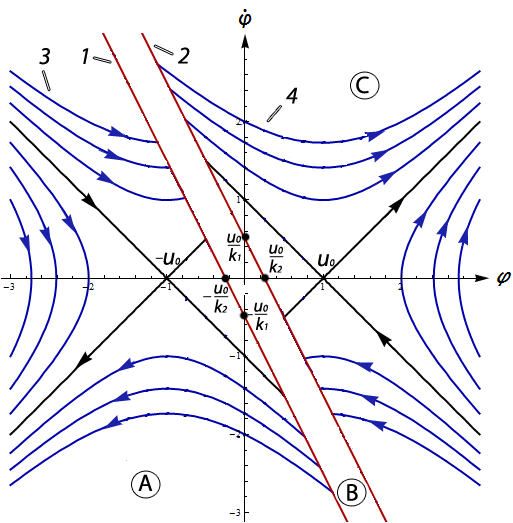
Рис. 12 Фазовые траектории вне области притяжения ( )

Если совместить плоскости 11 и 12, то получим фазовый портрет системы

, 2146214\* MERGEFORMAT (.)

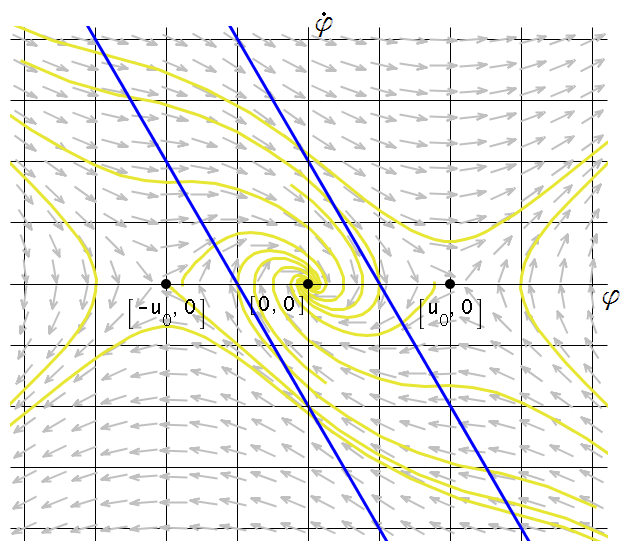
Рис. 13 Фазовый портрет 6214 ( )

Оглавление

Фазовый портрет системы 6214 приведен на рисунке 13. Анализ этого фазового портрета показывает, что стабилизировать положение равновесия маятника с помощью управления 6214 удается не при любых начальных условиях. Во-первых, в область притяжения В могут попасть не все траектории из областей А и С. Во-вторых, не все траектории, попадающие в область притяжения В, остаются в ней и стремятся к началу координат.

Таким образом, для того, чтобы управление вида 6204 давало решение задачи стабилизации 6201, необходимо подобрать специальным образом значения коэффициентов и . Но и тогда задачу стабилизации можно решить не при всех начальных условиях.

Определение

Областью управляемости называется область начальных значений параметров состояния, для которых система управляема, то есть можно построить управление, переводящее систему из заданного начального положения в заданное конечное.

Область управляемости задачи 6201 представляет собой часть фазовой плоскости, ограниченную асимптотами семейств гипербол

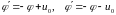, 2156215\* MERGEFORMAT (.)

то есть полосу

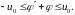2166216\* MERGEFORMAT (.)

На рисунке 12 видно, что в случае, когда 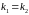, границы 1 и 2 области притяжения 6205 параллельны границам 6215 области управляемости, и тогда область притяжения целиком лежит внутри области управляемости. В этом случае все фазовые траектории из области 6216 попадают в область притяжения. Никакие другие в область притяжения не попадают. Кроме того, при траектории из области притяжения не выходят. Последнее видно на рисунке 14.

Таким образом, решение поставленной в данном параграфе задачи 6201 возможно при значениях скорости 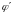и отклонения маятника, удовлетворяющих в начальный момент времени следующему условию

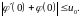2176217\* MERGEFORMAT (.)

Оглавление

Управление, обеспечивающее стабилизацию неустойчивого положения равновесия, будет

. 2186218\* MERGEFORMAT (.)

На рисунке 14 показаны область управляемости, она ограничена прямыми 3 и 4, и область притяжения, она обозначена серым цветом. Графики на рисунке 14 построены для системы 6218 при значении . При уменьшении значения , область притяжения увеличивается.

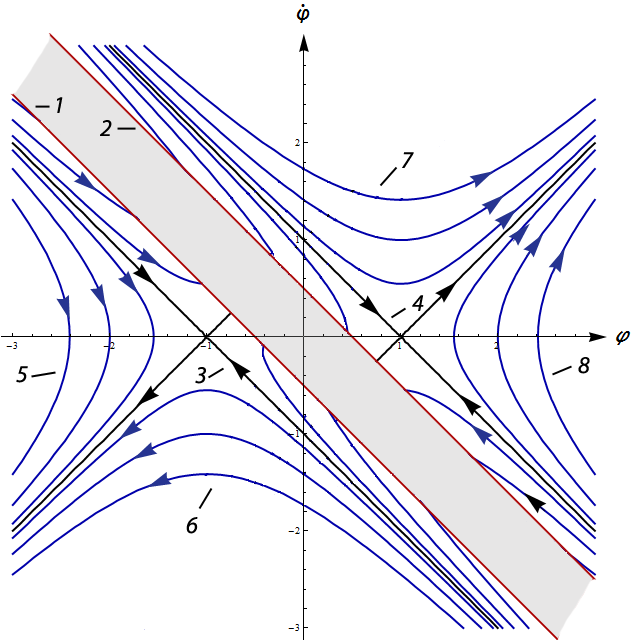
Рис. 14 Область притяжения и область управляемости системы 6218

( )

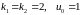Согласно 6218 поведение фазовых траекторий внутри области притяжения подчиняется уравнению 6206. При значениях соответствующее характеристическое уравнение имеет вид

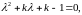2196219\* MERGEFORMAT (.)

его корни

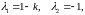2206220\* MERGEFORMAT (.)

Оглавление

действительны и отрицательны, а тривиальное решение системы 6218 представляет собой устойчивый узел.

При значении корни характеристического уравнения 6220 равны

,

и фазовые траектории в области притяжения имеют вид вырожденного устойчивого узла. Соответствующая картина приведена на рисунке 15. На нем цифрами 1,2 показаны границы области притяжения 6205. Цифры 3,4,5 соответствуют фазовым траекториям, причем прямая 3-это асимптота.

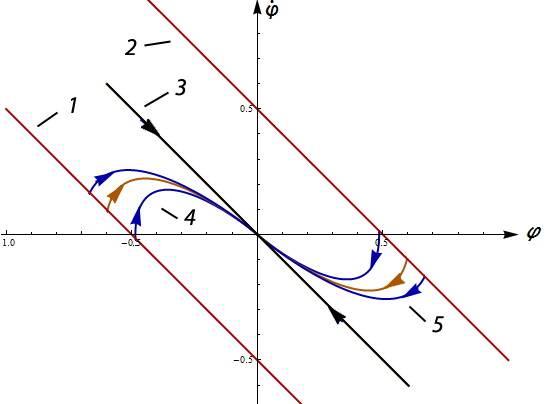
Рис. 15 Траектории внутри области притяжения ( )

Общая картина фазового портрета дана на рисунке 16. Границы области управляемости даны черным цветом, а границы области притяжения синим.

Оглавление

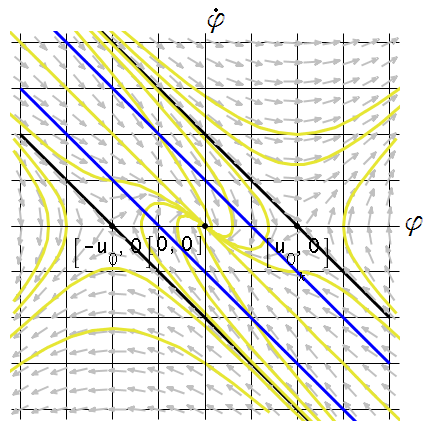
Рис. 16 Фазовый портрет системы 6218 ( )