Лекция № 4 Первый и второй замечательные пределы

4.1.Теорема (первый замечательный предел)

Предел отношения синуса бесконечно малой дуги к длине дуги равен единице.

Доказательство:

Возьмем круг радиуса 1. Обозначим радианную меру угла АОС через х.

Р ассмотрим: 1)Пусть ; можно считать, что , т.к. ; _;

, площадь сектора

_{разделим это неравенство на 1/2sinx >0}

Т.к. то по теореме о 2-х милиционерах .

2) Пусть , тогда при .

Замечание1:

Замечание 2: действительно, при

Замечание 3:

Покажем это: , тогда получим

, но так как , то .

4.2. Примеры

Вычислить следующие пределы:

1. .

Решение. Очевидно, что при x→π/2 числитель и знаменатель дроби стремиться к нулю. Разложив числитель и знаменатель на множители и сократив дробь на получим

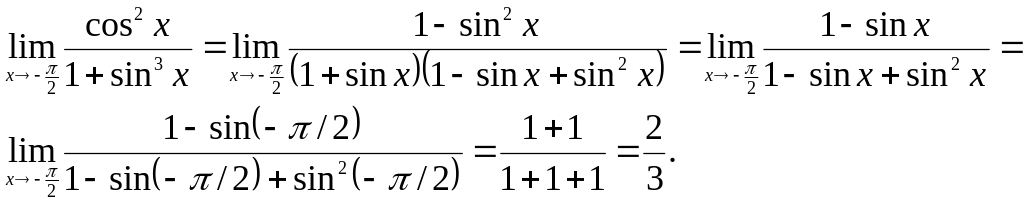
2.

Решение. Преобразуя заданное выражение и используя первый замечательный предел, получим

3.

Решение. Имеем

4.

Решение. Преобразовав разность косинусов в произведение, получим

5.

Решение. Введём подстановку тогда если х→π/2, то y→0. Следовательно,

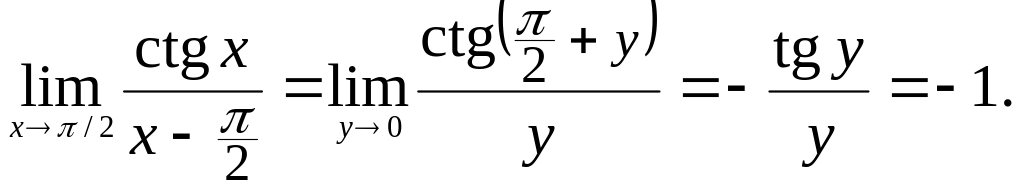
6.

Решение. Полагая arcsin 3x=α, имеем sin α =3x. Произведём преобразования:

Тогда получим

4.3. Второй замечательный предел. Число e.

Имеет место соотношение ( второй замечательный предел)

, или

Число e– иррациональное (e ≈ 2,718…, более точное значение e ≈ 2,7182818).

Показательная функция с основанием e называется экспоненциальной. . Для нее также применяется обозначение y=exp(x).

4.4. Примеры

Вычислить следующие пределы:

7.

Решение. Выполнив преобразования и используя формулу (2), находим

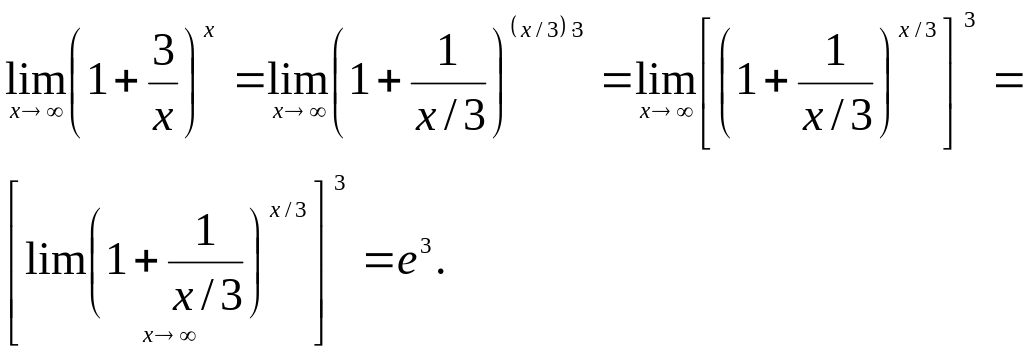
8.

Решение. Выполнив преобразования и применив второй замечательный предел, найдём

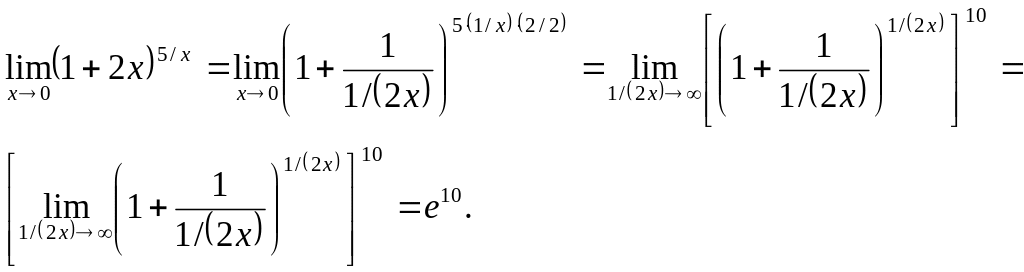
9.

Решение. Выполнив преобразования, найдём

4.5. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции

Сумма, разность и произведение двух бесконечно малых функций есть функция бесконечно малая. Отношение же двух бесконечно малых функций может вести себя различным образом, т.е: быть конечным числом, быть бесконечно малой, или бесконечно большой функцией, или вообще не стремиться ни к какому пределу.

Пусть и - бесконечно малые функции при . Рассмотрим .

1. Если конечное 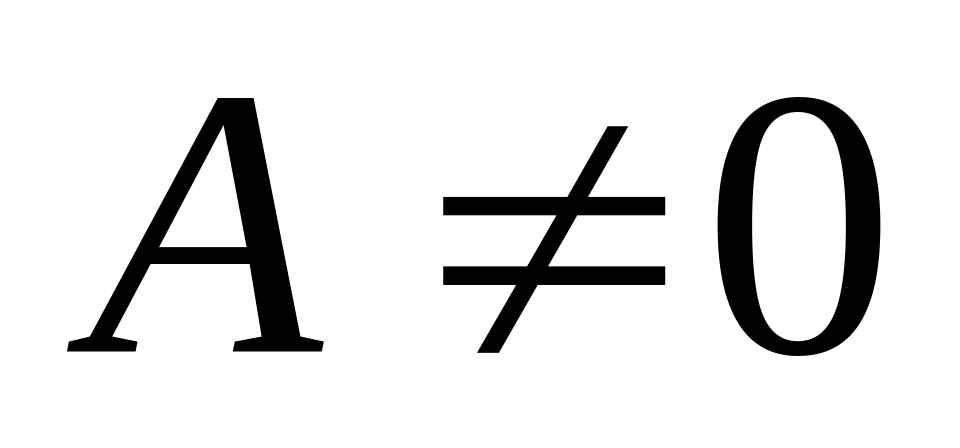, то и - б.м. одного порядка малости;

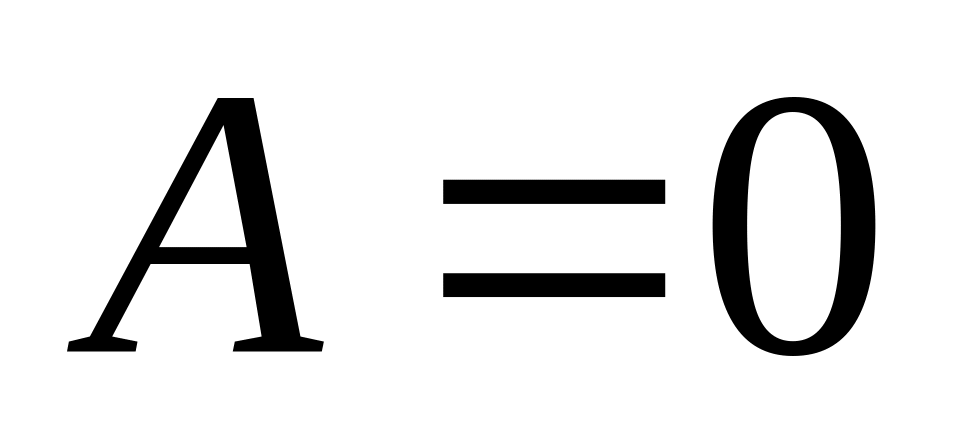2. Если конечное , то порядок б.м. выше порядка .

3. Если 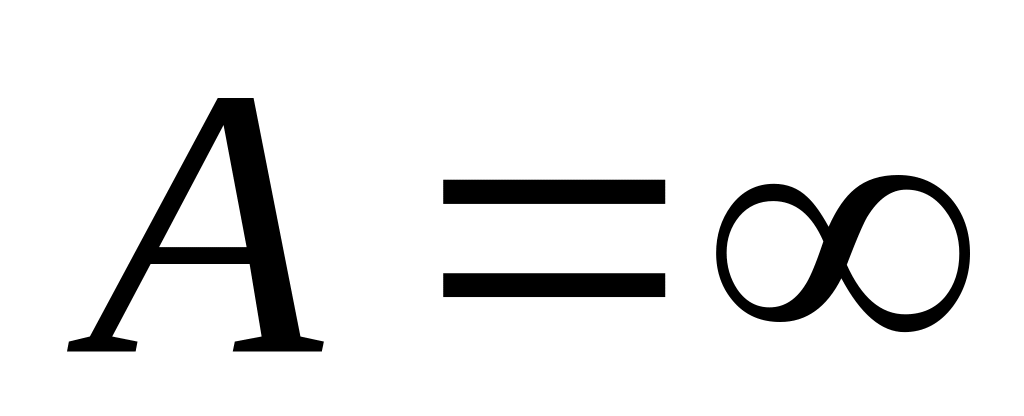, то ниже порядка .

4. Если не существует, то и несравнимые б.м. функции.

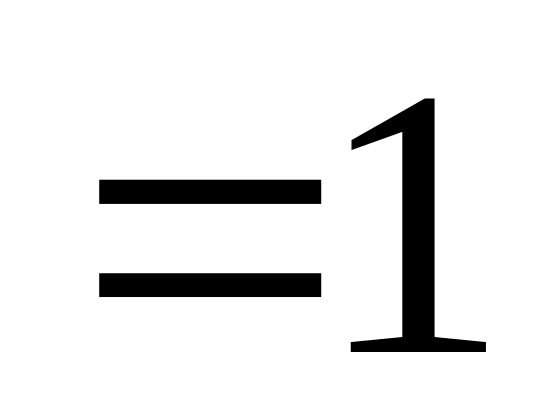5. Если , то и эквивалентные б.м. при функции (обозначается ).

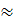4.6. Теоремы об эквивалентных бесконечно малых функциях

Теорема 1: Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой функцией.

Теорема 2: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Теорема 3. Сумма конечного числа бесконечно малых функций разного порядка эквивалентна слагаемому высшего порядка.

4.7. Таблица эквивалентных функций (при

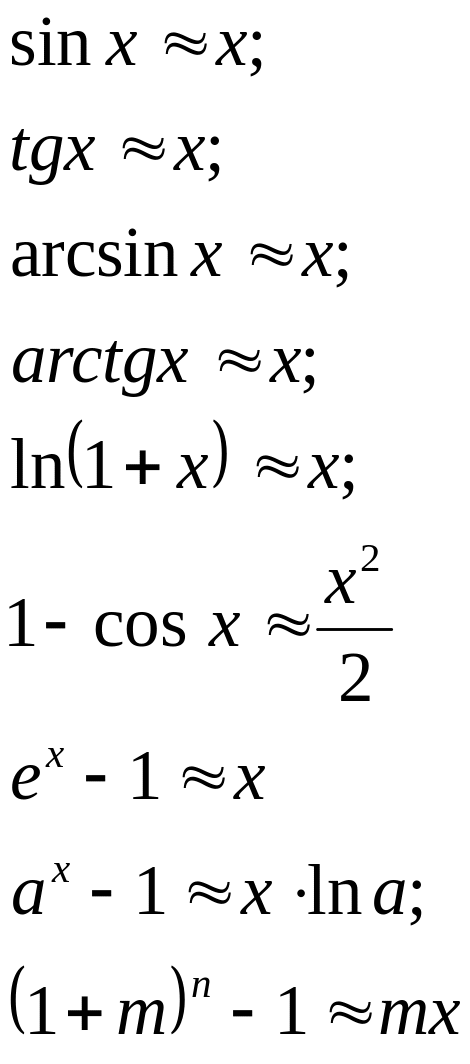
Лекция №5

Непрерывность функций

5.1. Непрерывность функции в точке

Функция y=f(x) называется непрерывной в точке х₀, если она определена в этой точке, существует предел функции в этой точке и он равен значению функции в этой точке, т.е.

.

Это равенство означает выполнение трех условий: